Products: ABAQUS/Standard ABAQUS/Explicit ABAQUS/CAE
Anisotropic yield and/or creep:
can be used for materials that exhibit different yield and/or creep behavior in different directions;
is introduced through user-defined stress ratios that are applied in Hill's potential function;
can be used only in conjunction with the metal plasticity and, in ABAQUS/Standard, the metal creep material models;
is available for the nonlinear isotropic/kinematic hardening model in ABAQUS/Explicit (“Models for metals subjected to cyclic loading,” Section 18.2.2); and
can be used in conjunction with the models of progressive damage and failure in ABAQUS/Explicit (“Damage and failure for ductile metals: overview,” Section 19.2.1) to specify different damage initiation criteria and damage evolution laws that allow for the progressive degradation of the material stiffness and the removal of elements from the mesh.
Anisotropic yield or creep behavior is modeled through the use of yield or creep stress ratios, 
. In the case of anisotropic yield the yield ratios are defined with respect to a reference yield stress, 
(given for the metal plasticity definition), such that if 
is applied as the only nonzero stress, the corresponding yield stress is 
. The plastic flow rule is defined below.
In the case of anisotropic creep the are creep ratios used to scale the stress value when the creep strain rate is calculated. Thus, if 
is the only nonzero stress, the equivalent stress, 
, used in the user-defined creep law is 
.
Yield and creep stress ratios can be defined as constants or as tabular functions of temperature and predefined field variables. A local orientation must be used to define the direction of anisotropy (see “Orientations,” Section 2.2.5).
| Input File Usage: | Use the following option to define the yield or creep stress ratios: |
*POTENTIAL This option must appear immediately after the *PLASTIC or the *CREEP material option data to which it applies. Thus, if anisotropic metal plasticity and anisotropic creep behavior are both required, the *POTENTIAL option must appear twice in the material definition, once after the metal plasticity data and again after the creep data. |
| ABAQUS/CAE Usage: | Use one of the following models: |
Property module: material editor: |
Hill's potential function is a simple extension of the Mises function, which can be expressed in terms of rectangular Cartesian stress components as
and N are constants obtained by tests of the material in different orientations. They are defined as 
is the measured yield stress value when is applied as the only nonzero stress component; is the user-defined reference yield stress specified for the metal plasticity definition; 
, 
, 
, 
, 
, and 
are anisotropic yield stress ratios; and 
. The six yield stress ratios are, therefore, defined as follows (in the order in which you must provide them): 
The flow rule is
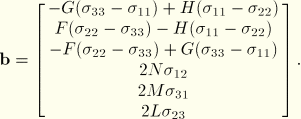
| Input File Usage: | Use both of the following options: |
*PLASTIC *POTENTIAL |
| ABAQUS/CAE Usage: | Property module: material editor: Mechanical |
For anisotropic creep in ABAQUS/Standard Hill's function can be expressed as
is the equivalent stress and F, G, H, L, M, and N are constants obtained by tests of the material in different orientations. The constants are defined with the same general relations as those used for anisotropic yield (above); however, the reference yield stress, , is replaced by the uniaxial equivalent deviatoric stress, (found in the creep law), and , , 
, , 
, and are referred to as “anisotropic creep stress ratios.” The six creep stress ratios are, therefore, defined as follows (in the order in which they must be provided): 
in each direction that will be used to scale the stress value when the creep strain rate is calculated. If all six values are set to unity, isotropic creep is obtained.| Input File Usage: | Use both of the following options: |
*CREEP *POTENTIAL |
| ABAQUS/CAE Usage: | Property module: material editor: Mechanical |
As discussed above, Hill's anisotropic plasticity potential is defined in ABAQUS from user input consisting of ratios of yield stress in different directions with respect to a reference stress. However, in some cases, such as sheet metal forming applications, it is common to find the anisotropic material data given in terms of ratios of width strain to thickness strain. Mathematical relationships are then necessary to convert the strain ratios to stress ratios that can be input into ABAQUS.
In sheet metal forming applications we are generally concerned with plane stress conditions. Consider 
to be the “rolling” and “cross” directions in the plane of the sheet; z is the thickness direction. From a design viewpoint, the type of anisotropy usually desired is that in which the sheet is isotropic in the plane and has an increased strength in the thickness direction, which is normally referred to as transverse anisotropy. Another type of anisotropy is characterized by different strengths in different directions in the plane of the sheet, which is called planar anisotropy.
In a simple tension test performed in the x-direction in the plane of the sheet, the flow rule for this potential (given above) defines the incremental strain ratios (assuming small elastic strains) as
Similarly, for a simple tension test performed in the y-direction in the plane of the sheet, the incremental strain ratios are
A transversely anisotropic material is one where 
. If we define in the metal plasticity model to be equal to 
,
(isotropic material), 
and the Mises isotropic plasticity model is recovered.In the case of planar anisotropy 
and 
are different and 
will all be different. If we define in the metal plasticity model to be equal to ,
, 
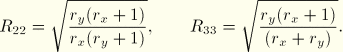
and the Mises isotropic plasticity model is recovered.Thus far, we have only considered loading applied along the axes of anisotropy. To derive a more general anisotropic model in plane stress, the sheet must be loaded in one other direction in its plane. Suppose we perform a simple tension test at an angle 
to the x-direction; then, from equilibrium considerations we can write the nonzero stress components as
is the applied tensile stress. Substituting these values in the flow equations and assuming small elastic strains yields 
Assuming small geometrical changes, the width strain increment (the increment of strain at right angles to the direction of loading, ) is written as
is 
One of the more commonly performed tests is that in which the loading direction is at 45°. In this case
If is equal to in the metal plasticity model, 
. 
are as defined before for transverse or planar anisotropy and, using the relationships above,
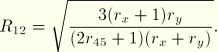
In ABAQUS/Explicit anisotropic yield can be used in conjunction with the models of progressive damage and failure discussed in “Damage and failure for ductile metals: overview,” Section 19.2.1. The capability allows for the specification of one or more damage initiation criteria, including ductile, shear, forming limit diagram (FLD), forming limit stress diagram (FLSD), and Müschenborn-Sonne forming limit diagram (MSFLD) criteria. After damage initiation, the material stiffness is degraded progressively according to the specified damage evolution response. The model offers two failure choices, including the removal of elements from the mesh as a result of tearing or ripping of the structure. The progressive damage models allow for a smooth degradation of the material stiffness, making them suitable for both quasi-static and dynamic situations.
| Input File Usage: | Use the following options: |
*PLASTIC *DAMAGE INITIATION *DAMAGE EVOLUTION |
| ABAQUS/CAE Usage: | Property module: material editor: Mechanical |
There are cases when we need to study the behavior of a material that has already been subjected to some work hardening. For such cases ABAQUS allows you to prescribe initial conditions for the equivalent plastic strain, 
, by specifying the conditions directly (“Initial conditions,” Section 27.2.1).
| Input File Usage: | *INITIAL CONDITIONS, TYPE=HARDENING |
| ABAQUS/CAE Usage: | Initial equivalent plastic strain is not supported in ABAQUS/CAE. |
For more complicated cases, initial conditions can be defined in ABAQUS/Standard through user subroutine HARDINI.
| Input File Usage: | *INITIAL CONDITIONS, TYPE=HARDENING, USER |
| ABAQUS/CAE Usage: | User subroutine HARDINI is not supported in ABAQUS/CAE. |
Anisotropic yield can be defined for any element that can be used with the classical metal plasticity models in ABAQUS (“Classical metal plasticity,” Section 18.2.1) except one-dimensional elements in ABAQUS/Explicit (beams and trusses). In ABAQUS/Standard it can also be defined for any element that can be used with the linear kinematic hardening plasticity model (“Models for metals subjected to cyclic loading,” Section 18.2.2) but not with the nonlinear isotropic/kinematic hardening model. Likewise, anisotropic creep can be defined for any element that can be used with the classical metal creep model in ABAQUS/Standard (“Rate-dependent plasticity: creep and swelling,” Section 18.2.4).
The standard output identifiers available in ABAQUS (“ABAQUS/Standard output variable identifiers,” Section 4.2.1, and “ABAQUS/Explicit output variable identifiers,” Section 4.2.2) and all output variables associated with the creep model (“Rate-dependent plasticity: creep and swelling,” Section 18.2.4), classical metal plasticity models (“Classical metal plasticity,” Section 18.2.1), and the linear kinematic hardening plasticity model (“Models for metals subjected to cyclic loading,” Section 18.2.2) are available when anisotropic yield and creep are defined.
The following variables have special meaning if anisotropic yield and creep are defined:
PEEQ | Equivalent plastic strain, |
CEEQ | Equivalent creep strain, |
where 
is the initial equivalent plastic strain (zero or user-specified; see 