The previous section (“Damage initiation for fiber-reinforced composites,” Section 19.3.2) discussed the damage initiation in plane stress fiber-reinforced composites. This section will discuss the post-damage initiation behavior for cases in which a damage evolution model has been specified. Prior to damage initiation the material is linearly elastic, with the stiffness matrix of a plane stress orthotropic material. Thereafter, the response of the material is computed from

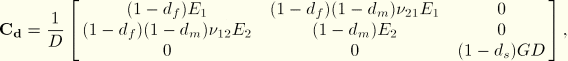
The damage variables , , and are derived from damage variables , , , and , corresponding to the four failure modes previously discussed, as follows:

Evolution of damage variables for each mode

To alleviate mesh dependency during material softening, ABAQUS introduces a characteristic length into the formulation, so that the constitutive law is expressed as a stress-displacement relation. The damage variable will evolve such that the stress-displacement behaves as shown in Figure 19.3.3–1 in each of the four failure modes. The positive slope of the stress-displacement curve prior to damage initiation corresponds to linear elastic material behavior; the negative slope after damage initiation is achieved by evolution of the respective damage variables according to the equations shown below.

Figure 19.3.3–1 Equivalent stress versus equivalent displacement.

Equivalent displacement and stress for each of the four damage modes are defined as follows:

Fiber tension :

Fiber compression :

Matrix tension :

Matrix compression :

For elements with a plane stress formulation the characteristic length, , is computed as a square root of the integration point area. The symbol in the equations above represents the Macaulay bracket operator, which is defined for every as .

After damage initiation (i.e., ) for the behavior shown in Figure 19.3.3–1, the damage variable for a particular mode is given by the following expression

where is the initial equivalent displacement at which the initiation criterion for that mode was met and is the displacement at which the material is completely damaged in this failure mode. The above relation is presented graphically in Figure 19.3.3–2.

Figure 19.3.3–2 Damage variable as a function of equivalent displacement.

The values of for the various modes depend on the elastic stiffness and the strength parameters specified as part of the damage initiation definition (see “Damage initiation for fiber-reinforced composites,” Section 19.3.2). For each failure mode you must specify the energy dissipated due to failure, , which corresponds to the area of the triangle OAC in Figure 19.3.3–3. The values of for the various modes depend on the respective values.

Unloading from a partially damaged state, such as point B in Figure 19.3.3–3, occurs along a linear path toward the origin in the plot of equivalent stress vs. equivalent displacement; this same path is followed back to point B upon reloading as shown in the figure.

Figure 19.3.3–3 Linear damage evolution.

Input File Usage:	Use the following option to define the damage evolution law:
	*DAMAGE EVOLUTION, TYPE=ENERGY, SOFTENING=LINEAR , , , where , , , and are energies dissipated during damage for fiber tension, fiber compression, matrix tension, and matrix compression failure modes, respectively.

ABAQUS/CAE Usage:

Property module: material editor: MechanicalDamage for Fiber-Reinforced CompositesHashin Damage: SuboptionsDamage Evolution: Type: Energy: Softening: Linear

You have control over how ABAQUS treats elements with severe damage. By default, the upper bound to all damage variables at a material point is. You can reduce this upper bound as discussed in “Controlling element deletion and maximum degradation for materials with damage evolution” in “Section controls,” Section 21.1.4.

By default, an element is removed (deleted) once damage variables for all failure modes at all material points reach (see “Controlling element deletion and maximum degradation for materials with damage evolution” in “Section controls,” Section 21.1.4). If an element is removed, the output variable STATUS is set to zero for the element, and it offers no resistance to subsequent deformation. However, the element still remains in the ABAQUS model and is visible in the Visualization module of ABAQUS/CAE (ABAQUS/Viewer). You can choose to suppress the display of removed elements by creating a display group consisting of all elements with STATUS equal to 1.0 (see “Selection methods for creating or editing a display group,” Section 52.2.2 of the ABAQUS/CAE User's Manual).

Alternatively, you can specify that an element should remain in the model even after all of the damage variables reach . In this case, once all the damage variables reach the maximum value, the stiffness, , remains constant (see the expression for earlier in this section).

Material models exhibiting softening behavior and stiffness degradation often lead to severe convergence difficulties in implicit analysis programs, such as ABAQUS/Standard. You can overcome some of these convergence difficulties by using the viscous regularization scheme, which causes the tangent stiffness matrix of the softening material to be positive for sufficiently small time increments.

In this regularization scheme a viscous damage variable is defined by the evolution equation:

The approximate amount of energy associated with viscous regularization over the whole model or over an element set is available using output variable ALLCD.

Defining viscous regularization coefficients

You can specify different values of viscous coefficients for different failure modes.

Input File Usage:	Use the following option to define viscous coefficients:
	*DAMAGE STABILIZATION , , , where , , , are viscosity coefficients for fiber tension, fiber compression, matrix tension, and matrix compression failure modes, respectively.

ABAQUS/CAE Usage:

Property module: material editor: MechanicalDamage for Fiber-Reinforced CompositesHashin Damage: SuboptionsDamage Stabilization

Applying a single viscous coefficient

Alternatively, you can specify the viscous coefficients as part of a section controls definition. In this case the same viscous coefficient will be applied to all failure modes. For more information, see “Using viscous regularization with cohesive elements, connector elements, and elements with plane stress formulations in ABAQUS/Standard” in “Section controls,” Section 21.1.4.

If stiffness proportional damping is specified in combination with the damage evolution law for fiber-reinforced materials, ABAQUS/Standard calculates the damping stresses using the damaged elastic stiffness.