
Products: ABAQUS/Standard ABAQUS/CAE
Warning: The information in this section is provided for users who may wish to adjust the convergence criteria for the solution of nonlinear systems. In most cases these criteria need not be adjusted.

In nonlinear problems the governing balance equations must be solved iteratively. This section describes:
the solution method for nonlinear problems (Newton's method);
the field equations that can be solved by ABAQUS/Standard;
the criteria used to establish convergence of each iteration during the solution;
“severe discontinuity” iterations; and
the line search algorithm, which can be used to improve the robustness of the Newton method.

Where possible, ABAQUS/Standard uses Newton's method to solve nonlinear problems. In some cases it uses an exact implementation of Newton's method, in the sense that the Jacobian of the system is defined exactly, and quadratic convergence is obtained when the estimate of the solution is within the radius of convergence of the algorithm. In other cases the Jacobian is approximated so that the iterative method is not an exact Newton method. For example, some material and surface interface models (such as nonassociated flow plasticity models or Coulomb friction) create a nonsymmetric Jacobian matrix, but you may choose to approximate this matrix by its symmetric part.
Many problems exhibit discontinuous behavior. A common example is contact: at a particular point on a surface, the contact constraint is either present or absent. Another (usually less severe) example is strain reversal in plasticity at a point where the material is yielding.
You can choose to use the quasi-Newton technique for a particular step (described in “Quasi-Newton solution technique,” Section 2.2.2 of the ABAQUS Theory Manual) instead of the standard Newton method for solving nonlinear equations.
The quasi-Newton technique can save substantial computational cost in some cases by reducing the number of times the Jacobian matrix is factorized. Generally it is most successful when the system is large and many iterations are needed per increment or when the stiffness matrix is not changing much from iteration to iteration (such as in a dynamic analysis using implicit time integration or in a small-displacement analysis with local plasticity). It can be used only for symmetric systems of equations; therefore, it cannot be used when the unsymmetric solver is specified for a step (see “Procedures: overview,” Section 6.1.1), nor can it be used for procedures that always produce an unsymmetric system of equations, such as “Fully coupled thermal-stress analysis,” Section 6.5.4, and “ABAQUS/Aqua analysis,” Section 6.10.1. In addition, it cannot be used for a static Riks procedure (see “Unstable collapse and postbuckling analysis,” Section 6.2.4).
The quasi-Newton method works well in combination with the line search method (see “Improving the efficiency of the solution by using the line search algorithm). Line searches help to prevent divergence of equilibrium iterations resulting from the inexact Jacobian produced by the quasi-Newton method. The line search method is activated by default for steps that use the quasi-Newton method. You can override this action by specifying line search controls.
You can specify the number of quasi-Newton iterations allowed before the kernel matrix is reformed. The default number of iterations is 8. Additional matrix reformations may occur automatically during the iteration process depending on the convergence behavior. Since quadratic convergence is not expected during quasi-Newton iterations, the logarithmic rate of convergence check is not applied during the time incrementation. Furthermore, the iteration count used in the time incrementation is a weighted sum of quasi-Newton iterations, with the weight factor depending on whether or not a kernel matrix has been reformed.
| Input File Usage: | *SOLUTION TECHNIQUE, TYPE=QUASI-NEWTON, REFORM KERNEL=n |
| ABAQUS/CAE Usage: | Step module: step editor: Other: Solution technique: Quasi-Newton, Number of iterations allowed before the kernel matrix is reformed: n |
Alternatively, you can choose to use the separated technique instead of the standard Newton method for solving nonlinear equations for fully coupled thermal-stress and coupled thermal-electrical procedures.
The separated technique (described in “Fully coupled thermal-stress analysis,” Section 6.5.4, and “Coupled thermal-electrical analysis,” Section 6.6.2) approximates the Jacobian by eliminating interfield coupling terms and can save substantial computational cost in cases where there is relatively weak coupling between the fields.
| Input File Usage: | *SOLUTION TECHNIQUE, TYPE=SEPARATED |
| ABAQUS/CAE Usage: | Step module: step editor: Other: Solution technique: Separated |

Field equations can be modeled separately or fully coupled. Some fields in ABAQUS/Standard can only have linear response. Each field is discretized by using basic nodal variables (the degrees of freedom at the nodes of the finite element model) such as the components of the displacement in a continuum stress analysis problem. Each field has a conjugate “flux.”
The fields and conjugate fluxes available in ABAQUS/Standard are as follows:
| Basic problem | Field | Conjugate flux |
|---|---|---|
| Stress analysis: | Displacement, | Force, |
| Force equilibrium | Warping, w | Bimoment, W |
| Structural stress analysis: | Rotation, | Moment, |
| Moment equilibrium | ||
| Heat transfer analysis | Temperature, | Heat flux, q |
| Acoustic analysis (linear only) | Acoustic pressure, u | Rate of change of fluid volumetric flux |
| Pore liquid flow analysis | Pore liquid pressure, u | Pore liquid volumetric flux, q |
| Hydrostatic fluid modeling | Fluid pressure, p | Fluid volume, V |
| Mass diffusion analysis | Normalized concentration, | Mass concentration volumetric flux, Q |
| Piezoelectric analysis | Electrical potential, | Electrical charge, q |
| Electric conduction analysis | Electrical potential, | Electrical current, J |
| Mechanism analysis (connector elements with material flow degree of freedom) | Material flow | Material flux |
In some cases the problem also involves constraint equations. In ABAQUS/Standard the following constraints are included by using Lagrange multipliers:
| Problem | Constraint variable | Constraint |
|---|---|---|
| Hybrid solid | Pressure stress | Volumetric strain compatibility |
| Hybrid beam | Axial force | Axial strain compatibility |
| Hybrid beam | Transverse shear force | Transverse shear strain compatibility |
| Distributing coupling | Force | Coupling displacement compatibility |
| Distributing coupling | Moment | Coupling rotation compatibility |
| Contact | Normal pressure | Surface penetration |
| Contact with Lagrange friction | Shear stress | Relative shear sliding |
If the penalty method is used, the contact normal pressure Lagrange multiplier may not be present.
In a general problem several (possibly nonlinear) coupled field equations of types ![]() must be solved and several different (possibly nonlinear) constraints of type
must be solved and several different (possibly nonlinear) constraints of type ![]() must be satisfied simultaneously. For example, in a structural problem in which hybrid beam elements are used,
must be satisfied simultaneously. For example, in a structural problem in which hybrid beam elements are used, ![]() might represent the displacement field and the equilibrium equations for the conjugate force and
might represent the displacement field and the equilibrium equations for the conjugate force and ![]() might represent the rotation field and the equilibrium equations for the conjugate moment, while
might represent the rotation field and the equilibrium equations for the conjugate moment, while ![]() represents axial strain compatibility and
represents axial strain compatibility and ![]() represents transverse shear strain compatibility.
represents transverse shear strain compatibility.

The default solution control parameters defined in ABAQUS/Standard are designed to provide reasonably optimal solution of complex problems involving combinations of nonlinearities as well as efficient solution of simpler nonlinear cases. However, the most important consideration in the choice of the control parameters is that any solution accepted as “converged” is a close approximation to the exact solution of the nonlinear equations. In this context “close approximation” is interpreted rather strictly by engineering standards when the default value is used, as described below.
You can reset many solution control parameters related to the tolerances used for field equations. If you define less strict convergence criteria, results may be accepted as converged when they are not sufficiently close to the exact solution of the system. Use caution when resetting solution control parameters. Lack of convergence is often due to modeling issues, which should be resolved before changing the accuracy controls.
You can select the type of equation for which the solution control parameters are being defined; for example, you can redefine the default controls for the displacement field and warping degree of freedom equilibrium equations only. By default, the solution control parameters will apply to all active fields in the model. See “Defining tolerances for field equations” in “Commonly used control parameters,” Section 7.2.2, for details.
| Input File Usage: | *CONTROLS, PARAMETERS=FIELD, FIELD=field |
| ABAQUS/CAE Usage: | Step module: Other |
Each field, ![]() , that is active in the problem is tested for convergence of the field equations. The following measures are used in deciding if an increment has converged:
, that is active in the problem is tested for convergence of the field equations. The following measures are used in deciding if an increment has converged:
![]()
The largest residual in the balance equation for field ![]() .
.
![]()
The largest change in a nodal variable of type ![]() in the increment.
in the increment.
![]()
The largest correction to any nodal variable of type ![]() provided by the current Newton iteration.
provided by the current Newton iteration.
![]()
The largest error in a constraint of type j.
![]()
The instantaneous magnitude of the flux for field ![]() at time t, averaged over the entire model (spatial average flux). This average is by default defined by the fluxes that the elements apply to their nodes and any externally defined fluxes:
at time t, averaged over the entire model (spatial average flux). This average is by default defined by the fluxes that the elements apply to their nodes and any externally defined fluxes:
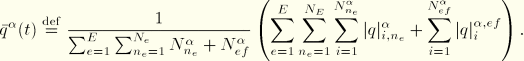
![]()
An overall time-averaged value of the typical flux for field ![]() so far during this step including the current increment. Normally,
so far during this step including the current increment. Normally, ![]() is defined as
is defined as ![]() averaged over all the increments in the step in which
averaged over all the increments in the step in which ![]() is nonzero. The
is nonzero. The ![]() for the current increment is recalculated after every iteration of the current increment.
for the current increment is recalculated after every iteration of the current increment.
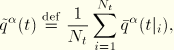
Alternatively, you can define a value for the average flux in the step, ![]() . In this case,
. In this case, ![]() throughout the step.
throughout the step.
At the start of the step, ![]() is normally the value from the previous step (except for Step 1, when
is normally the value from the previous step (except for Step 1, when ![]() by default). Alternatively, you can define an initial value for the time average flux,
by default). Alternatively, you can define an initial value for the time average flux, ![]() , as described in “Modifying the initial time average flux” in “Commonly used control parameters,” Section 7.2.2.
, as described in “Modifying the initial time average flux” in “Commonly used control parameters,” Section 7.2.2. ![]() retains its initial value until an iteration is completed for which
retains its initial value until an iteration is completed for which ![]() , at which time we redefine
, at which time we redefine ![]() . (If
. (If ![]() is defined, the value defined for
is defined, the value defined for ![]() is ignored.)
is ignored.)
![]()
The time-averaged value of the largest flux corresponding to the field ![]() during this step, excluding the current increment.
during this step, excluding the current increment.
![]()
The largest flux corresponding to the field ![]() during the current iteration.
during the current iteration.
The time-averaged value of the flux (![]() ) is computed from the spatial average of the flux (
) is computed from the spatial average of the flux (![]() ) at various instants in time. In some situations where only a small part of the model is active (the fluxes over the rest of the model are zero or very small), the spatial average of a flux over the entire model can be very small when compared to the spatial average over the active part of the model. Over a period of time this can result in a small value for the time-averaged value of the flux and in turn may lead to a convergence criterion that is very strict by engineering standards. To avoid such an excessively strict convergence criterion, ABAQUS/Standard uses an algorithm to determine the active parts of a model at any given instant.
) at various instants in time. In some situations where only a small part of the model is active (the fluxes over the rest of the model are zero or very small), the spatial average of a flux over the entire model can be very small when compared to the spatial average over the active part of the model. Over a period of time this can result in a small value for the time-averaged value of the flux and in turn may lead to a convergence criterion that is very strict by engineering standards. To avoid such an excessively strict convergence criterion, ABAQUS/Standard uses an algorithm to determine the active parts of a model at any given instant.
During an iteration any flux ![]() is treated as inactive, and the corresponding degree of freedom is also marked inactive.
is treated as inactive, and the corresponding degree of freedom is also marked inactive. ![]() is the time-averaged value of the largest flux in the model during the current step. The default value of
is the time-averaged value of the largest flux in the model during the current step. The default value of ![]() is 10–5; you can redefine this parameter.
is 10–5; you can redefine this parameter.
At the end of an iteration the largest flux in the model during the current iteration (![]() ) is compared with the time-averaged value of the largest flux (
) is compared with the time-averaged value of the largest flux (![]() ). If
). If ![]() , the spatial average is computed over only the active parts of the model; if
, the spatial average is computed over only the active parts of the model; if ![]() , all inactive parts of the model are reclassified as active and the spatial average is computed over the entire model. The appropriate spatial average of the flux obtained in this manner is then used to compute the time-averaged flux
, all inactive parts of the model are reclassified as active and the spatial average is computed over the entire model. The appropriate spatial average of the flux obtained in this manner is then used to compute the time-averaged flux ![]() that is used in the convergence criterion. Setting
that is used in the convergence criterion. Setting ![]() forces the spatial averages of a flux to be always computed over the entire model.
forces the spatial averages of a flux to be always computed over the entire model.
If you specify a value for the average flux in the step, ![]() ,
, ![]() throughout the step.
throughout the step.
Most nonlinear engineering calculations will be sufficiently accurate if the error in the residuals is less than ![]() %. Therefore, ABAQUS/Standard normally uses
%. Therefore, ABAQUS/Standard normally uses
![]()
![]()
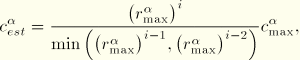
![]()
The superscripts i, ![]() , and
, and ![]() refer to the iteration number, and
refer to the iteration number, and ![]() refers to the largest residual in field
refers to the largest residual in field ![]() at the start of the first iteration of the increment. See “Commonly used control parameters,” Section 7.2.2, for more details on specifying
at the start of the first iteration of the increment. See “Commonly used control parameters,” Section 7.2.2, for more details on specifying ![]() .
.
In some cases there may be zero flux in the equations of type ![]() anywhere in the model during some increments. Zero flux is defined as
anywhere in the model during some increments. Zero flux is defined as ![]() , where, as discussed earlier,
, where, as discussed earlier, ![]() has a default value of 10–5 and the solution for field
has a default value of 10–5 and the solution for field ![]() is accepted if
is accepted if ![]() . If not,
. If not, ![]() is compared to
is compared to ![]() , and convergence for field
, and convergence for field ![]() is accepted when
is accepted when ![]() . The default value of
. The default value of ![]() is 10–3; you can redefine this parameter.
is 10–3; you can redefine this parameter.
Cases may arise where more than one field is active in the model yet there is negligible response in some of the fields in some increments. If some type of physical conversion factor, ![]() , exists between active fields
, exists between active fields ![]() and
and ![]() ,
, ![]() in the above paragraph can be replaced by
in the above paragraph can be replaced by ![]() for those particular increments where
for those particular increments where ![]() is deemed too small (
is deemed too small (![]() ) to be used realistically as part of the convergence criteria for field
) to be used realistically as part of the convergence criteria for field ![]() . An example of
. An example of ![]() is a characteristic length to convert between force and moment.
is a characteristic length to convert between force and moment.
Here, ![]() is a factor calculated by ABAQUS/Standard based on the problem definition and the fields involved and
is a factor calculated by ABAQUS/Standard based on the problem definition and the fields involved and ![]() is a field conversion ratio that you can define. The default value for
is a field conversion ratio that you can define. The default value for ![]() is 1.0. Currently, this concept is used only for converting between the fields associated with forces and moments, when
is 1.0. Currently, this concept is used only for converting between the fields associated with forces and moments, when ![]() represents a characteristic element length.
represents a characteristic element length.
Linear cases do not require more than one equilibrium iteration per increment. If
![]()
You can define ![]() ; it is intended to be very small. The default value of
; it is intended to be very small. The default value of ![]() is 10–8. Any case that passes such a stringent comparison of the largest residual with the average flux magnitude in each field is considered linear and does not require further iteration. If this requirement is satisfied at some iteration after the first, the solution is accepted without any check on the size of the correction to the solution.
is 10–8. Any case that passes such a stringent comparison of the largest residual with the average flux magnitude in each field is considered linear and does not require further iteration. If this requirement is satisfied at some iteration after the first, the solution is accepted without any check on the size of the correction to the solution.
In some cases quadratic convergence of the iterations is not possible because the Jacobian of the Newton scheme is approximated. If after ![]() iterations the convergence rate is only linear, ABAQUS/Standard uses a looser tolerance,
iterations the convergence rate is only linear, ABAQUS/Standard uses a looser tolerance,
![]()
You can define ![]() , which is 2 × 10–2 by default. You can also define
, which is 2 × 10–2 by default. You can also define ![]() (by default,
(by default, ![]() ; see “Controlling iteration”).
; see “Controlling iteration”).
Convergence also requires that
![]()
When the active field is the displacement, the convergence criterion requiring the largest displacement correction to be small relative to the maximum displacement increment (![]() ) is ignored when the maximum displacement increment itself is very small, as defined by
) is ignored when the maximum displacement increment itself is very small, as defined by ![]() , where
, where ![]() is the characteristic element length. The default value for
is the characteristic element length. The default value for ![]() is 10–8; you can redefine this parameter.
is 10–8; you can redefine this parameter.

Each increment of a nonlinear solution will usually be solved by multiple equilibrium iterations. The number of iterations may become excessive, in which case the increment size should be reduced and the increment attempted again. On the other hand, if successive increments are solved with a minimum number of iterations, the increment size may be increased. You can specify a number of time incrementation control parameters; some of them are described in this section, while the remainder are described in “Time integration accuracy in transient problems,” Section 7.2.4.
| Input File Usage: | *CONTROLS, PARAMETERS=TIME INCREMENTATION |
| ABAQUS/CAE Usage: | Step module: Other |
ABAQUS/Standard may have trouble with the element calculations because of excessive distortion in large-displacement problems or because of very large plastic strain increments. If this occurs and automatic time incrementation has been chosen, the increment will be attempted again with a time increment of ![]() times the current time increment, where you can define
times the current time increment, where you can define ![]() . By default,
. By default, ![]() . If fixed time stepping has been chosen, the analysis will terminate with an error message.
. If fixed time stepping has been chosen, the analysis will terminate with an error message.
Sometimes the increment is too large for the solution to converge at all—the initial state is outside the “radius of convergence” of the Newton method. This condition can be detected by observing the behavior of the largest residuals, ![]() . In some cases these will not decrease from iteration to iteration throughout an iteration sequence that leads to convergence, but we assume that, if they fail to decrease over two consecutive iterations, the iterations should be abandoned. Thus, if
. In some cases these will not decrease from iteration to iteration throughout an iteration sequence that leads to convergence, but we assume that, if they fail to decrease over two consecutive iterations, the iterations should be abandoned. Thus, if
![]()
With automatic time stepping the increment is begun again, using a time increment of ![]() times the previous attempt, where you can define
times the previous attempt, where you can define ![]() . By default,
. By default, ![]() . This subdivision continues until a successful time increment is found or the minimum time increment allowed has failed, in which case the job ends with an error message. Using the line search algorithm with
. This subdivision continues until a successful time increment is found or the minimum time increment allowed has failed, in which case the job ends with an error message. Using the line search algorithm with ![]() sometimes helps in such cases (see “Improving the efficiency of the solution by using the line search algorithm”).
sometimes helps in such cases (see “Improving the efficiency of the solution by using the line search algorithm”).
In case quadratic convergence cannot be obtained, the logarithmic rate of convergence,
![]()
You can define the values of ![]() ,
, ![]() , and
, and ![]() . By default,
. By default, ![]() ,
, ![]() , and
, and ![]() =0.5.
=0.5.
When automatic time incrementation is chosen, the effectiveness of the nonlinear equation solution is used in the selection of the next time increment (in addition to the time integration accuracy criteria discussed in “Time integration accuracy in transient problems,” Section 7.2.4). If no more than ![]() iterations are required in two consecutive increments, the time increment may be increased by a factor of
iterations are required in two consecutive increments, the time increment may be increased by a factor of ![]() . If an increment converges but takes more than
. If an increment converges but takes more than ![]() iterations, the next time increment is reduced to
iterations, the next time increment is reduced to ![]() times the current time increment. You can define the values of
times the current time increment. You can define the values of ![]() ,
, ![]() ,
, ![]() , and
, and ![]() . By default,
. By default, ![]() ,
, ![]() ,
, ![]() , and
, and ![]() .
.
At each increment after the first increment of a nonlinear analysis step ABAQUS/Standard estimates the solution to the increment by extrapolating the solution from the previous increment (or increments). By default, 100% linear extrapolation is used (1% for the Riks method). Extrapolation is abandoned if
![]()
You can turn this extrapolation scheme off for a particular step—see “Procedures: overview,” Section 6.1.1.

Strain constraint convergence in “hybrid” elements is checked by comparing the largest error in each strain constraint, ![]() , with an absolute tolerance for the corresponding error,
, with an absolute tolerance for the corresponding error, ![]() . The magnitudes of these errors are reported in the message (.msg) file after each iteration as “compatibility errors.” For example, the volumetric compatibility error is a measure of the accuracy with which the incompressibility constraint is satisfied. Since nonlinearity in constraint equations is generally reflected in the field equations in the same problem, no attempt is made to estimate convergence rates in these constraint equations: we assume that the measures of convergence rate in the field equations are sufficient.
. The magnitudes of these errors are reported in the message (.msg) file after each iteration as “compatibility errors.” For example, the volumetric compatibility error is a measure of the accuracy with which the incompressibility constraint is satisfied. Since nonlinearity in constraint equations is generally reflected in the field equations in the same problem, no attempt is made to estimate convergence rates in these constraint equations: we assume that the measures of convergence rate in the field equations are sufficient.
You can define the ![]() (
(![]() ,
, ![]() , and
, and ![]() ). By default, all of the
). By default, all of the ![]() = 10–5.
= 10–5.
| Input File Usage: | *CONTROLS, PARAMETERS=CONSTRAINTS |
| ABAQUS/CAE Usage: | Step module: Other |

ABAQUS/Standard distinguishes between regular, equilibrium iterations (in which the solution varies smoothly) and severe discontinuity iterations (SDIs) in which abrupt changes in stiffness occur. By default, ABAQUS/Standard will continue to iterate until no severe discontinuities occur and the equilibrium (flux) tolerances are satisfied. Alternatively, ABAQUS/Standard can convert the severe discontinuities into force residuals and iterate until the residual tolerances are satisfied. This latter method is particularly effective if the contact conditions are only weakly determined and contact “chattering” occurs or if a large number of severe discontinuity iterations are required to settle the contact conditions. For more information on the SDI conversion capability, see “Severe discontinuities in ABAQUS/Standard” in “Procedures: overview,” Section 6.1.1.
In implicit dynamic analysis with “hard” contact, the average time of all contact changes in the increment is estimated and the time incrementation is interrupted to solve impact equations at that time. In implicit dynamic analysis with softened contact, no impact equations are solved; however, if the soft contact constraint compatibility is not satisfied within the given tolerance, a severe discontinuity iteration is forced. See “Intermittent contact/impact,” Section 2.4.2 of the ABAQUS Theory Manual, for details on intermittent contact in dynamic problems.
You can define the soft contact compatibility tolerance.
| Input File Usage: | *CONTROLS, PARAMETERS=CONSTRAINTS , , , |
| ABAQUS/CAE Usage: | Step module: Other |
A limit, ![]() , is placed on the number of iterations caused by severe discontinuities in an increment. If more than
, is placed on the number of iterations caused by severe discontinuities in an increment. If more than ![]() iterations are required for severe discontinuities, the increment is begun again with a time increment size of
iterations are required for severe discontinuities, the increment is begun again with a time increment size of ![]() times the abandoned increment size (for automatic time incrementation). If fixed time incrementation was chosen, the analysis terminates with an error message. You can define the values of
times the abandoned increment size (for automatic time incrementation). If fixed time incrementation was chosen, the analysis terminates with an error message. You can define the values of ![]() and
and ![]() . By default,
. By default, ![]() and
and ![]() .
.
| Input File Usage: | *CONTROLS, PARAMETERS=TIME INCREMENTATION , , , , , , |
| ABAQUS/CAE Usage: | Step module: Other |
Since SDI conversion yields a residual force even if severe discontinuities occur, it is not necessary for ABAQUS to use the maximum number of severe discontinuity iterations to decide whether it should continue iterating or cut back the increment size. Instead, ABAQUS applies more sophisticated criteria involving both changes in the residual force and the number of severe discontinuities from one increment to the next. This makes it possible to run contact problems that require large numbers of contact changes without having to change the control parameters. It is still possible to set a limit, ![]() , for the maximum number of severe discontinuity iterations; by default,
, for the maximum number of severe discontinuity iterations; by default, ![]() , which in practice should always be more than the actual number of iterations required.
, which in practice should always be more than the actual number of iterations required.
| Input File Usage: | *CONTROLS, PARAMETERS=TIME INCREMENTATION , , , , , , , , , , |
| ABAQUS/CAE Usage: | Step module: Other |

ABAQUS/Standard provides the option of including a “line search” algorithm. The purpose of the line search is to improve the robustness of the Newton or quasi-Newton methods. By default, the line search is active only for steps that use the quasi-Newton method. During equilibrium iterations where residuals are large, the line search algorithm scales the correction to the solution by a line search scale factor, ![]() . An iterative process is used to find the value of
. An iterative process is used to find the value of ![]() that minimizes the component of the residual vector in the direction of the correction vector; this component is called
that minimizes the component of the residual vector in the direction of the correction vector; this component is called ![]() , where j is the line search iteration number. Each line search iteration requires one pass through the ABAQUS/Standard element loop but does not require any operations using the global stiffness matrix.
, where j is the line search iteration number. Each line search iteration requires one pass through the ABAQUS/Standard element loop but does not require any operations using the global stiffness matrix.
It is usually sufficient to determine ![]() only to modest accuracy. There are several controls used to limit this accuracy. A maximum of
only to modest accuracy. There are several controls used to limit this accuracy. A maximum of ![]() line search iterations are performed. There is a limit on the allowable range of
line search iterations are performed. There is a limit on the allowable range of ![]() :
:
![]()
![]()
You can define the values of ![]() ,
, ![]() ,
, ![]() ,
, ![]() , and
, and ![]() . By default,
. By default, ![]() = 0 with the Newton method, and
= 0 with the Newton method, and ![]() =5 with the quasi-Newton method. Set
=5 with the quasi-Newton method. Set ![]() to a nonzero value to activate the line search algorithm or to zero to forcibly deactivate line search. Default values for the additional line search parameters are
to a nonzero value to activate the line search algorithm or to zero to forcibly deactivate line search. Default values for the additional line search parameters are ![]() = 1.0,
= 1.0, ![]() = 0.0001,
= 0.0001, ![]() = 0.25, and
= 0.25, and ![]() = 0.10. These defaults are chosen to achieve modest accuracy for the line search scale factor, while minimizing the additional cost of line search iterations. More agressive line searching can be beneficial in some simulations, especially when many nonlinear iterations and/or cutbacks are needed to resolve sharp discontinuities in the solution. In these cases you could try allowing more line search iterations (
= 0.10. These defaults are chosen to achieve modest accuracy for the line search scale factor, while minimizing the additional cost of line search iterations. More agressive line searching can be beneficial in some simulations, especially when many nonlinear iterations and/or cutbacks are needed to resolve sharp discontinuities in the solution. In these cases you could try allowing more line search iterations (![]() =10) and requiring more accuracy in the line search scale factor (
=10) and requiring more accuracy in the line search scale factor ( ![]() =0.01). This may result in more line search iterations but fewer nonlinear iterations and cutbacks and an overall reduction in solution cost.
=0.01). This may result in more line search iterations but fewer nonlinear iterations and cutbacks and an overall reduction in solution cost.
| Input File Usage: | *CONTROLS, PARAMETERS=LINE SEARCH |
| ABAQUS/CAE Usage: | Step module: Other |