Products: ABAQUS/Standard ABAQUS/CAE
ABAQUS offers a damage model enabling you to predict the onset of damage and to model damage evolution for elastic-brittle materials with anisotropic behavior. The model is primarily intended to be used with fiber-reinforced materials since they typically exhibit such behavior.
This damage model requires specification of the following:
the undamaged response of the material, which must be linearly elastic (see “Linear elastic behavior,” Section 17.2.1);
a damage initiation criterion (see “Progressive damage and failure,” Section 19.1.1, and “Damage initiation for fiber-reinforced composites,” Section 19.3.2); and
a damage evolution response, including a choice of element removal (see “Progressive damage and failure,” Section 19.1.1, and “Damage evolution and element removal for fiber-reinforced composites,” Section 19.3.3).
Damage is characterized by the degradation of material stiffness. It plays an important role in the analysis of fiber-reinforced composite materials. Many such materials exhibit elastic-brittle behavior; that is, damage in these materials is initiated without significant plastic deformation. Consequently, plasticity can be neglected when modeling behavior of such materials.
The fibers in the fiber-reinforced material are assumed to be parallel, as depicted in Figure 19.3.1–1. You must specify material properties in a local coordinate system defined by the user. The lamina is in the 1–2 plane, and the local 1 direction corresponds to the fiber direction. You must specify the undamaged material response using one of the methods for defining an orthotropic linear elastic material (“Linear elastic behavior,” Section 17.2.1); the most convenient of which is the method for defining an orthotropic material in plane stress (“Defining orthotropic elasticity in plane stress” in “Linear elastic behavior,” Section 17.2.1). However, the material response can also be defined in terms of the engineering constants or by specifying the elastic stiffness matrix directly.
The ABAQUS anisotropic damage model is based on the work of Matzenmiller et. al (1995), Hashin and Rotem (1973), Hashin (1980), and Camanho and Davila (2002).
Four different modes of failure are considered:
fiber rupture in tension;
fiber buckling and kinking in compression;
matrix cracking under transverse tension and shearing; and
matrix crushing under transverse compression and shearing.
In ABAQUS the onset of damage is determined by the initiation criteria proposed by Hashin and Rotem (1973) and Hashin (1980), in which the failure surface is expressed in the effective stress space (the stress acting over the area that effectively resists the force). These criteria are discussed in detail in “Damage initiation for fiber-reinforced composites,” Section 19.3.2.
The response of the material is computed from
is the strain and 
is the elasticity matrix, which reflects any damage and has the form
, 
reflects the current state of fiber damage, 
reflects the current state of matrix damage, 
reflects the current state of shear damage, 
is the Young's modulus in the fiber direction, 
is the Young's modulus in the direction perpendicular to the fibers, 
is the shear modulus, and 
and 
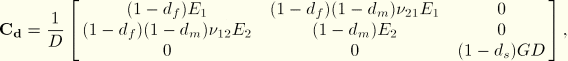
are Poisson's ratios.The evolution of the elasticity matrix due to damage is discussed in more detail in “Damage evolution and element removal for fiber-reinforced composites,” Section 19.3.3; that section also discusses:
options for treating severe damage (“Maximum degradation and choice of element removal” in “Damage evolution and element removal for fiber-reinforced composites,” Section 19.3.3); and
viscous regularization (“Viscous regularization in ABAQUS/Standard” in “Damage evolution and element removal for fiber-reinforced composites,” Section 19.3.3).
The fiber-reinforced composite damage model must be used with elements with a plane stress formulation, which include plane stress, shell, continuum shell, and membrane elements.
Hashin, Z., and A. Rotem, “A Fatigue Criterion for Fiber-Reinforced Materials,” Journal of Composite Materials, vol. 7, pp. 448–464, 1973.
Hashin, Z., “Failure Criteria for Unidirectional Fiber Composites,” Journal of Applied Mechanics, vol. 47, pp. 329–334, 1980.
Matzenmiller, A., J. Lubliner, and R. L. Taylor, “A Constitutive Model for Anisotropic Damage in Fiber-Composites,” Mechanics of Materials, vol. 20, pp. 125–152, 1995.
Camanho, P. P., and C. G. Davila, “Mixed-Mode Decohesion Finite Elements for the Simulation of Delamination in Composite Materials,” NASA/TM-2002–211737, pp. 1–37, 2002.
