5.2.3 Coulomb friction

Products: ABAQUS/Standard ABAQUS/Explicit
An extended version of the classical isotropic Coulomb friction model is provided in ABAQUS for use with all contact analysis cababilities. The extensions include an additional limit on the allowable shear stress, anisotropy, and the definition of a “secant” friction coefficient.
The standard Coulomb friction model assumes that no relative motion occurs if the equivalent frictional stress
is less than the critical stress,
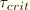
, which is proportional to the contact pressure,

, in the form
where

is the friction coefficient that can be defined as a function of the contact pressure,

; the slip rate,
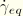
; the average surface temperature at the contact point; and the average field variables at the contact point. Rate-dependent friction cannot be used in a static Riks analysis since velocity is not defined. In ABAQUS it is possible to put a limit on the critical stress:
where
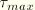
is user-specified. If the equivalent stress is at the critical stress
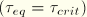
, slip can occur. If the friction is isotropic, the direction of the slip and the frictional stress coincide, which is expressed in the form
where
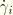
is the slip rate in direction
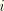
and
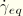
is the magnitude of the slip velocity,
As will be shown later, the same laws can be used for anisotropic friction after some simple transformations.
The above behavior can be modeled in ABAQUS/Standard in two different ways. By default, the condition of no relative motion is approximated by stiff elastic behavior. The stiffness is chosen such that the relative motion from the position of zero shear stress is bounded by a value 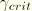 . (In the ABAQUS Analysis User's Manual
. (In the ABAQUS Analysis User's Manual 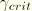 is referred to as the allowable maximum elastic slip.) The critical slip value,
is referred to as the allowable maximum elastic slip.) The critical slip value, 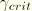 , can be specified by the user. If it is not specified by the user,
, can be specified by the user. If it is not specified by the user, 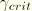 is, by default, set to 0.5% of the average length of all contact elements in the model. It is worth noting that this approximate implementation method can also be considered an implementation of a nonlocal friction model; that is, a friction model for which the Coulomb condition is not applied pointwise but weighted over a small area with a so-called mollifying function (Zhong, 1989). See Oden and Pires (1983) for further discussion of nonlocal friction models.
is, by default, set to 0.5% of the average length of all contact elements in the model. It is worth noting that this approximate implementation method can also be considered an implementation of a nonlocal friction model; that is, a friction model for which the Coulomb condition is not applied pointwise but weighted over a small area with a so-called mollifying function (Zhong, 1989). See Oden and Pires (1983) for further discussion of nonlocal friction models.
Optionally, the relative motion in the absence of slip can be made exactly zero with the use of a Lagrange multiplier formulation. Although this procedure appears attractive because of the exact sticking constraint, it has two disadvantages:
The additional Lagrange multipliers increase the cost of the analysis.
The presence of rigid constraints tends to slow or sometimes prevent convergence of the Newton solution scheme used in ABAQUS/Standard. This is likely to occur in areas where contact conditions change.
A special case of friction in ABAQUS/Standard is so-called rough friction, where it is assumed that there is no bound on the shear stress; that is, no relative motion can occur as long as the surfaces are in contact. Rough friction is implemented with the Lagrange multiplier method.
In ABAQUS/Explicit the relative motion in the absence of slip is always equal to zero if the kinematic contact algorithm is used with hard tangential surface behavior; at the end of each increment the positions of the nodes on the contact surfaces are adjusted so that the relative motion is zero. With the penalty contact algorithm in ABAQUS/Explicit the relative motion in the absence of slip is equal to the friction force divided by the penalty stiffness.
Elastic stick formulation

In the elastic stick formulation in ABAQUS/Standard, the “elastic” tangential slip 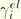 is defined as the reversible relative tangential motion from the point of zero shear stress. The elastic slip is related to the interface shear stress with the relation
is defined as the reversible relative tangential motion from the point of zero shear stress. The elastic slip is related to the interface shear stress with the relation
where
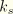
is the (current) “stiffness in stick,” which follows from the relation
Since
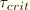
may be dependent on contact pressure, slip rate, average surface temperature at the contact point, and field variables,
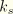
may change during the analysis. The behavior remains elastic as long as the equivalent stress does not exceed the critical stress; hence,
Consistent linearization of this expression yields
The contributions from the contact pressure are nonsymmetric for the second case. Since the slip rate is zero in the elastic stick formulation, derivatives with respect to the slip velocity are not needed.
The above expressions hold if the equivalent shear stress remains less than the critical stress. If the equivalent stress exceeds the critical stress, slip must be taken into consideration so that the condition 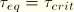 is satisfied. Let the starting situation be characterized by the elastic slip
is satisfied. Let the starting situation be characterized by the elastic slip 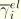 . The critical stress at the end of the increment follows from the contact pressure,
. The critical stress at the end of the increment follows from the contact pressure,  , and the slip rate,
, and the slip rate, 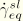 .
.
Let the (as yet unknown) elastic slip at the end of the increment be 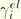 and the slip increment be
and the slip increment be 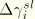 . Consistency requires that
. Consistency requires that
and the shear stress at the end of the increment follows from the elasticity relation,
The slip increment is related to the stress at the end of the increment with the backward difference approach:
With these equations and the critical stress equality
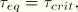
it is possible to solve for
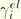
,
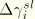
, and
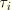
. Elimination of
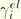
and
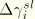
from the above equations yields,
or
It is convenient to define the “elastic predictor strain”
which simplifies the expression for the stress to
Substitution in the critical stress equality yields
where
Substitution in the expression for
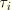
and introduction of the normalized slip direction
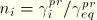
furnishes the final result
Here
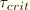
is a function of the slip rate, which is obtained with
where

is the time increment in a static analysis. In the case of dynamics

is scaled by the Hilber-Hughes-Taylor time integration operator parameters,
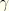
and
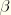
.
For the iterative solution scheme this equation must be linearized. Some straightforward algebra yields
With the expression for the equivalent slip the final result is
In this case the unsymmetric terms may have a strong effect on the speed of convergence of the Newton scheme. Hence, use of the unsymmetric equations solver is strongly recommended for the analysis of problems in which sliding friction occurs. In the case of dynamics

is scaled by the Hilber-Hughes-Taylor time integration operator parameters.
Frictional stress due to forced sliding in static analysis

If the user specifies different velocities for two bodies in contact as a predefined field, it is assumed that the slip velocity follows from the prescribed motion and is independent of the displacement values. The frictional stresses then follow from
where
and
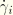
are the tangential slip velocities derived from the user-defined fields (
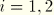
).
Friction contributions for complex eigenvalue extraction analysis

At the contact nodes at which the velocity differential is imposed, the linearized shear stress can be expressed in the following form:
In the equation above the first term is generated by the friction forces acting in the direction perpendicular to the direction of slip. The third term exists if the friction coefficient depends on velocity. In the complex eigenvalue extraction analysis both terms contribute to the damping matrix. The second term contributes to the stiffness matrix.
Viscous stick formulation for steady-state transport

For steady-state transport a viscous stick formulation is used. In this case the “viscous” tangential slip rate, 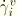 , is related to the interface shear stress by
, is related to the interface shear stress by
where
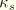
is the “stick viscosity,” which follows from the relation
The allowable viscous slip is defined as a fraction of the relative tangential velocity
where
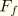
is a user-defined slip tolerance,
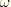
is the angular spinning velocity, and
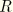
is the radius of a point on the contact surface in the undeformed configuration.
Exact stick formulation

In ABAQUS/Standard Lagrange multipliers are used to enforce exact sticking conditions. A constraint term enforced with Lagrange multipliers 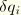 is added to the virtual work statement:
is added to the virtual work statement:
where
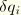
is a Lagrange multiplier. By taking the rate of change of
Equation 5.2.3–4, the rate of virtual work is obtained:
where the last term results from a nonlinear relation between nodal displacements and relative motion
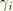
. This term is nonzero only for contact with finite sliding (see
“Finite-sliding interaction between deformable bodies,” Section 5.1.2, and
“Finite-sliding interaction between a deformable and a rigid body,” Section 5.1.3).
To obtain a complete formulation, a relationship between 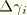 ,
, 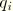 , and
, and 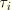 must be defined. For sticking conditions a suitable relation is
must be defined. For sticking conditions a suitable relation is
with
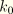
a reference stiffness selected internally in ABAQUS. The reference stiffness can be considered to model a spring that is in parallel to the sticking constraint. Since the constraint prevents relative motion, the reference stiffness has no physical significance and is added only to eliminate zero terms on the diagonal of the stiffness matrix that could cause equation solver problems. The variational and rate forms of the equation for
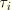
are readily obtained as
Substitution in
Equation 5.2.3–5 yields
If the element is slipping, 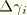 can take an arbitrary value. Consequently the terms involving
can take an arbitrary value. Consequently the terms involving 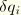 in Equation 5.2.3–4 and Equation 5.2.3–5 vanish. With the backward difference method, the frictional stress is obtained as
in Equation 5.2.3–4 and Equation 5.2.3–5 vanish. With the backward difference method, the frictional stress is obtained as
and the linearized form is
The rate of virtual work can, hence, be written in the form
Observe that for two-dimensional problems the term involving
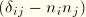
vanishes. In the case of dynamics

is scaled by the Hilber-Hughes-Taylor time integration operator parameters.
To determine whether an element sticks or slips, the following tests are used. If the element is currently sticking, it is checked whether the magnitude of the frictional stress exceeds the critical value. Hence, if
the state is changed to slipping.
If the element is slipping, the direction of slip is compared with the frictional stress 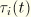 applied at the start of the iteration. If at the end of the iteration
applied at the start of the iteration. If at the end of the iteration
the state is changed to sticking.
Anisotropic friction

In anisotropic friction the friction coefficients in the two (principal) directions are different; hence, the critical shear stresses are different:
The two critical shear stresses are at the extreme points of the friction ellipse, given by the equation
This suggests definition of the scaled shear stresses,
where
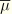
is the average friction coefficient defined by
Hence, the (scaled) equivalent frictional stress is defined by
and the average critical stress
where
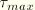
is the user-specified limiting shear stress, which is applied to the scaled shear stresses. No slip will occur if
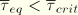
, and slip can occur if
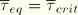
.
If slip occurs, it is assumed that the direction of slip is governed by an associated slip law:
Hence, scaled rates of slip are defined by
and the (scaled) equivalent slip rate
As a result, the direction of the scaled slip and the scaled shear stress coincide:
Since these equations have exactly the same structure as the equations for isotropic friction, the same solution algorithms can be used to get the incremental and linearized equations in terms of the scaled stress and slip. The actual stresses are readily obtained from the scaled stresses with
Equation 5.2.3–10, and the linearized equations are scaled with the same factors.
In the anisotropic elastic stick formulation, it is assumed that the stiffness in stick in terms of the scaled stress and slip is constant:
hence, the scaled stress is related to the scaled elastic slip by the relation
In terms of the actual stress and strain in the 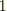 - and
- and 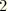 -directions, this implies
-directions, this implies
with
Hence, the anisotropy in terms of the stiffness in stick is more pronounced than the anisotropy in terms of critical stress.
Viscous damping

In addition to the friction models described above, ABAQUS allows for the definition of a “viscous” shear stress 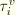 that is proportional to the relative tangential velocity
that is proportional to the relative tangential velocity 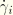 . This viscous damping in the tangential direction occurs if
. This viscous damping in the tangential direction occurs if
The viscous damping stress is proportional to the tangential damping coefficient
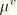
, which is a function of the overclosure as follows:
where
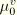
is the value of the tangential damping coefficient at zero overclosure and

is the fraction of the overclosure interval
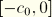
over which the damping coefficient is equal to
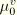
.
The virtual work contribution associated with the viscous shear stress is
The contribution to the stiffness matrix for the Newton solution is given by the linearized form of the virtual work contribution:
where
In static analysis the velocity is defined as the displacement increment divided by the time increment. Therefore, 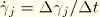 , and the stiffness contribution reduces to
, and the stiffness contribution reduces to
In the case of dynamics 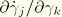 is defined by the dynamic time integration operator and the stiffness contribution can be written as
is defined by the dynamic time integration operator and the stiffness contribution can be written as
where
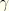
and
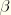
are the Hilber-Hughes-Taylor time integration operator parameters. Viscous damping cannot be used in a Riks analysis since velocity is not defined.

![]()
![]()
![]()
![]()
![]()
![]() . (In the ABAQUS Analysis User's Manual
. (In the ABAQUS Analysis User's Manual ![]() is referred to as the allowable maximum elastic slip.) The critical slip value,
is referred to as the allowable maximum elastic slip.) The critical slip value, ![]() , can be specified by the user. If it is not specified by the user,
, can be specified by the user. If it is not specified by the user, ![]() is, by default, set to 0.5% of the average length of all contact elements in the model. It is worth noting that this approximate implementation method can also be considered an implementation of a nonlocal friction model; that is, a friction model for which the Coulomb condition is not applied pointwise but weighted over a small area with a so-called mollifying function (Zhong, 1989). See Oden and Pires (1983) for further discussion of nonlocal friction models.
is, by default, set to 0.5% of the average length of all contact elements in the model. It is worth noting that this approximate implementation method can also be considered an implementation of a nonlocal friction model; that is, a friction model for which the Coulomb condition is not applied pointwise but weighted over a small area with a so-called mollifying function (Zhong, 1989). See Oden and Pires (1983) for further discussion of nonlocal friction models.
![]() is defined as the reversible relative tangential motion from the point of zero shear stress. The elastic slip is related to the interface shear stress with the relation
is defined as the reversible relative tangential motion from the point of zero shear stress. The elastic slip is related to the interface shear stress with the relation ![]()
![]()
![]()
![]() is satisfied. Let the starting situation be characterized by the elastic slip
is satisfied. Let the starting situation be characterized by the elastic slip ![]() . The critical stress at the end of the increment follows from the contact pressure,
. The critical stress at the end of the increment follows from the contact pressure, ![]() , and the slip rate,
, and the slip rate, ![]() .
.![]() and the slip increment be
and the slip increment be ![]() . Consistency requires that
. Consistency requires that ![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
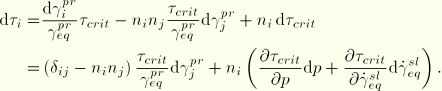

![]()
![]()
![]()

![]()

![]() , is related to the interface shear stress by
, is related to the interface shear stress by ![]()
![]()
![]()

![]() is added to the virtual work statement:
is added to the virtual work statement: ![]() ,
, ![]() , and
, and ![]() must be defined. For sticking conditions a suitable relation is
must be defined. For sticking conditions a suitable relation is ![]()
![]()
![]() can take an arbitrary value. Consequently the terms involving
can take an arbitrary value. Consequently the terms involving ![]() in Equation 5.2.3–4 and Equation 5.2.3–5 vanish. With the backward difference method, the frictional stress is obtained as
in Equation 5.2.3–4 and Equation 5.2.3–5 vanish. With the backward difference method, the frictional stress is obtained as ![]()
![]() applied at the start of the iteration. If at the end of the iteration
applied at the start of the iteration. If at the end of the iteration ![]()

![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]() - and
- and ![]() -directions, this implies
-directions, this implies ![]()
![]()

![]() that is proportional to the relative tangential velocity
that is proportional to the relative tangential velocity ![]() . This viscous damping in the tangential direction occurs if
. This viscous damping in the tangential direction occurs if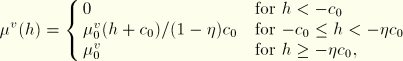
![]()
![]() , and the stiffness contribution reduces to
, and the stiffness contribution reduces to ![]()
![]() is defined by the dynamic time integration operator and the stiffness contribution can be written as
is defined by the dynamic time integration operator and the stiffness contribution can be written as ![]()