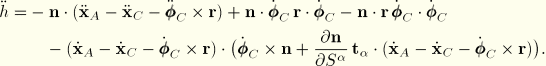Product: ABAQUS/Standard
ABAQUS/Standard provides two formulations for modeling the interaction between a deformable body and an arbitrarily shaped rigid body that may move during the history being modeled. The first is a small-sliding formulation in which the contacting surfaces can only undergo relatively small sliding relative to each other, but arbitrary rotation of the surfaces is permitted. This formulation is discussed in “Small-sliding interaction between bodies,” Section 5.1.1. The second is a finite-sliding formulation where separation and sliding of finite amplitude and arbitrary rotation of the surfaces may arise. This formulation is discussed in this section.
The finite-sliding rigid contact capability is implemented by means of a family of contact elements that ABAQUS automatically generates based on the data associated with the user-specified contact pairs. At each integration point these elements construct a measure of overclosure (penetration of the point on the surface of the deforming body into the rigid surface) and measures of relative shear sliding. These kinematic measures are then used, together with appropriate Lagrange multiplier techniques, to introduce surface interaction theories (contact and friction). A library of interaction theories is provided in ABAQUS—these may be thought of as a library of “surface constitutive models.” In this section we discuss only the kinematics of the interacting surfaces. The surface constitutive models are described in Chapter 4, “Mechanical Constitutive Theories.”
Let ![]() be a point on the deforming mesh, with current coordinates
be a point on the deforming mesh, with current coordinates ![]() . Let
. Let ![]() be the “rigid body reference node”—the node that defines the position of the rigid body—with current coordinates
be the “rigid body reference node”—the node that defines the position of the rigid body—with current coordinates ![]() . Let
. Let ![]() be the closest point on the surface of the rigid body to
be the closest point on the surface of the rigid body to ![]() at which the normal to the surface of the rigid body,
at which the normal to the surface of the rigid body, ![]() , passes through
, passes through ![]() . Define
. Define ![]() as the vector from
as the vector from ![]() to
to ![]() . The geometry described by these quantities is shown in Figure 5.1.3–1.
. The geometry described by these quantities is shown in Figure 5.1.3–1.
Let ![]() be the distance from
be the distance from ![]() to
to ![]() along
along ![]() : the “overclosure” of the surfaces. From the definitions introduced above,
: the “overclosure” of the surfaces. From the definitions introduced above,
![]()
Then if ![]() there is no contact between the surfaces at
there is no contact between the surfaces at ![]() , and no further surface interaction calculations need be done at this point. Here
, and no further surface interaction calculations need be done at this point. Here ![]() is the clearance below which contact occurs. For a “hard” surface
is the clearance below which contact occurs. For a “hard” surface ![]() , but ABAQUS/Standard also allows a “softened” surface to be introduced in which
, but ABAQUS/Standard also allows a “softened” surface to be introduced in which ![]() may be nonzero (although
may be nonzero (although ![]() is usually very small compared to other dimensions). If
is usually very small compared to other dimensions). If ![]() the surfaces are in contact. To enforce the contact constraint we will need the first variation of
the surfaces are in contact. To enforce the contact constraint we will need the first variation of ![]() ,
, ![]() , and its second variation,
, and its second variation, ![]() . These quantities are now derived.
. These quantities are now derived.
Let ![]() ,
, ![]() be locally orthogonal, distance measuring surface coordinates on the surface at
be locally orthogonal, distance measuring surface coordinates on the surface at ![]() . The
. The ![]() measure distance along the tangents
measure distance along the tangents ![]() to the surface at
to the surface at ![]() : these tangents are constructed according to the standard ABAQUS convention for such tangents to a surface in space. As the point
: these tangents are constructed according to the standard ABAQUS convention for such tangents to a surface in space. As the point ![]() and the rigid body move, the projected point
and the rigid body move, the projected point ![]() will move along. The movement consists of two parts: movement due to motion of the rigid body and motion relative to the body
will move along. The movement consists of two parts: movement due to motion of the rigid body and motion relative to the body
![]()
![]()
![]()
![]()
![]()
![]()
To obtain the second variation of ![]() , it will again be assumed that
, it will again be assumed that ![]() . In addition, it will be assumed that
. In addition, it will be assumed that ![]() , which is accurate for relatively “hard” contact. It then directly follows that
, which is accurate for relatively “hard” contact. It then directly follows that
![]()
![]()
![]()
![]()
![]()
![]()
![]()
Substitution of the last four expressions in the expression for the second variation yields
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
For dynamic applications we need the velocity and acceleration terms ![]() and
and ![]() to calculate impact forces and impulses correctly. These terms are
to calculate impact forces and impulses correctly. These terms are
![]()