
Product: ABAQUS/Standard
ABAQUS/Standard provides a surface-based capability for modeling fully saturated porous media. The surface-based capability can be used for small or finite sliding. Only flow normal to the surface is considered; tangential flow cannot be modeled.

Let ![]() and
and ![]() be the pore pressures at the two sides of the interface. It is at all times required that the pore pressures on opposite sides be equal:
be the pore pressures at the two sides of the interface. It is at all times required that the pore pressures on opposite sides be equal:
![]()
It is assumed that the interface is filled with fluid at all times. Hence, continuity requires that
![]()
![]()
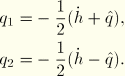

The contribution of the interfacial virtual work equation and its linearized form are first obtained in the general form including finite sliding. The equations are then specialized to the various formulations implemented in ABAQUS.
Since we want to achieve force and volume flow rate equilibrium at each side of the interface, as well as obtain continuity in the pore pressures, we add the following integral to the virtual work equation:
![]()
![]()
![]()
![]()
![]()
![]()

If the two sides are locally in contact, ![]() and
and ![]() ; therefore, the virtual work simplifies to
; therefore, the virtual work simplifies to
![]()
![]()

For steady-state analysis the transient terms can be omitted, and the terms involving fluid flow are written in rate form. In this case we can assume that the interface displacements vanish, which leads to the simplified virtual work contribution
![]()
![]()