
Products: ABAQUS/Standard ABAQUS/Explicit

AC1D2 AC1D3
AC2D3 AC2D4 AC2D4R AC2D6 AC2D8
AC3D4 AC3D6 AC3D8 AC3D8R AC3D10 AC3D15 AC3D20
The impedance boundary conditions are tested in this verification set. The model consists of a column of fluid 10 meters high with a cross-sectional area of 1 m. The first-order element models consist of 20 acoustic elements: 20 high and one in the cross-section. The second-order element models consist of 10 elements along the height direction.
One end of the column has a surface impedance imposed on it that is set equal to the characteristic impedance of the fluid column, ![]() , where
, where ![]() is the density of the fluid and
is the density of the fluid and ![]() is the speed of sound in the fluid. To simulate a nonreflecting boundary condition,
is the speed of sound in the fluid. To simulate a nonreflecting boundary condition, ![]() and
and ![]() 0 are set with the *IMPEDANCE option. The material used in these tests is air with the following properties: density,
0 are set with the *IMPEDANCE option. The material used in these tests is air with the following properties: density, ![]() 1.293 kg/m3; bulk modulus,
1.293 kg/m3; bulk modulus, ![]() 1.42176 × 105 N/m2; and
1.42176 × 105 N/m2; and ![]() 2.3323 × 10–3 m2s/kg.
2.3323 × 10–3 m2s/kg.
The other end of the column is excited by a harmonic pressure impulse of magnitude 1.0 N/m2. A steady-state dynamic analysis is performed in ABAQUS/Standard over a range of frequencies from 0 to 100 Hz. Transient simulations are also performed in ABAQUS/Explicit using an excitation frequency of 100 Hz. Different excitation frequencies can be tested by changing the parameters defined in the input files. The solution should represent a steady-state unattenuated wave moving in the positive ![]() -direction. No resonating frequencies should result; the maximum pressure throughout the column should consistently remain at a magnitude of 1.0 N/m2, and the phase should drop by 2
-direction. No resonating frequencies should result; the maximum pressure throughout the column should consistently remain at a magnitude of 1.0 N/m2, and the phase should drop by 2![]() radians over the distance of a wavelength,
radians over the distance of a wavelength, ![]() , where
, where ![]() is the excitation frequency in cycles per time.
is the excitation frequency in cycles per time.
With the meshes used in these tests, the results lie within 8% of the analytical solution for the first-order models and within 2% of the analytical solution for the second-order models. Finer meshes yield more accurate results.
AC1D2 elements.
AC1D3 elements.
AC2D3 elements.
AC2D4 elements.
AC2D6 elements.
AC2D8 elements.
AC3D4 elements.
AC3D6 elements.
AC3D8 elements.
AC3D10 elements.
AC3D15 elements.
AC3D20 elements.
ACAX3 elements.
ACAX4 elements.
ACAX6 elements.
ACAX8 elements.
ACAX3 elements.
ACAX4R elements.
AC2D3 elements.
AC2D4R elements.
AC3D4 elements.
AC3D6 elements.
AC3D8R elements.

Nonreflective boundaries on each of the acoustic elements, using the nonreflective default condition of both the *IMPEDANCE and *SIMPEDANCE options for steady-state dynamic analyses in ABAQUS/Standard. All elements are tested using the *STEADY STATE DYNAMICS, DIRECT prodecure; the AC2D4, AC2D8, and AC3D8 elements are also tested using the *STEADY STATE DYNAMICS, SUBSPACE PROJECTION procedure.
These tests model a sound source at ![]() 0 m in a tube with significant volumetric drag (air properties with
0 m in a tube with significant volumetric drag (air properties with ![]() 1400 Ns/m4) and a nonreflective end condition at
1400 Ns/m4) and a nonreflective end condition at ![]() 0.5 m at a frequency of 100 Hz. In each model the inward acceleration of the sound source is specified as the complex value
0.5 m at a frequency of 100 Hz. In each model the inward acceleration of the sound source is specified as the complex value ![]() , giving an inward velocity of 1 m/s. (The inward acceleration on a face is distributed to the nodes of the face as *CLOADs representing inward volume accelerations in the same way as pressure on a face would be distributed to the nodes of the face as *CLOADs representing nodal forces.) Because of the large drag, for good results at this frequency the constants
, giving an inward velocity of 1 m/s. (The inward acceleration on a face is distributed to the nodes of the face as *CLOADs representing inward volume accelerations in the same way as pressure on a face would be distributed to the nodes of the face as *CLOADs representing nodal forces.) Because of the large drag, for good results at this frequency the constants ![]() and
and ![]() must both be nonzero and must be based on the complex impedance of the medium.
must both be nonzero and must be based on the complex impedance of the medium.
The results are within 1% of the analytical results, which are given as comments in the input files. The analytical result for the high-drag tests predicts exponential decay of pressure magnitude and linear dependence of pressure phase.
AC1D2 elements.
AC1D3 elements.
AC2D3 elements.
AC2D4 elements.
AC2D6 elements.
AC2D8 elements.
AC3D4 elements.
AC3D6 elements.
AC3D8 elements.
AC3D10 elements.
AC3D15 elements.
AC3D20 elements.

Nonreflective boundaries on each of the acoustic elements, using the nonreflective default condition of *SIMPEDANCE with the IMPROVED PLANE parameter for transient dynamic analyses in ABAQUS/Standard and ABAQUS/Explicit. All elements are tested using either the *DYNAMIC procedure in ABAQUS/Standard or the *DYNAMIC, EXPLICIT procedure in ABAQUS/Explicit.
These tests model one-dimensional propagation of sound in situations where the acoustic waves exit the acoustic domain through oblique boundaries. Various elementary geometric shapes are tested. In all models sinusoidal acoustic pressure boundary conditions are applied on one face of the acoustic domain using either the *CLOAD or the *BOUNDARY option, in such a way as to result in one-dimensional acoustic wave propagation in the model. The models are created so as to force the acoustic waves to exit from the model via surfaces that possess either continuously varying normals or normals that are not oriented in the same direction as the propagation of the waves. On the exit surface the *SIMPEDANCE, IMPROVED PLANE option is used. The objective in all the models tested is to ensure that the problem remains one-dimensional and that there is no reflection of the acoustic waves back into the domain from the oblique boundary.
By studying the contour plots of the acoustic pressure (POR), it can be seen that the acoustic waves retain their directionality (one-dimensional and normal to the loading surface) even in the regions adjacent to the oblique boundary. For example, Figure 3.7.2–1 shows the contours of acoustic pressure in the case of a wedge-shaped model (brick45.inp) at the end of the analysis. As can be seen, the acoustic waves exit the boundary of the domain in exactly the same manner as they would if the boundary were normal to the outgoing plane waves.
Figure 3.7.2–1 Acoustic pressure contours illustrating the effect of using the *SIMPEDANCE, IMPROVED PLANE option to simulate a nonreflective boundary condition on an oblique surface.
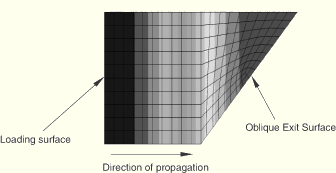
AC3D8 elements, oblique planar boundary.
AC3D8 elements, spherical boundary.
AC2D4 elements, oblique planar boundary.
AC2D4 elements, circular boundary.
AC3D4 elements, oblique planar boundary.
AC3D4 elements, spherical boundary.
AC2D3 elements, oblique planar boundary.
AC2D3 elements, circular boundary.
AC3D6 elements, oblique planar boundary.
AC3D8 elements, oblique planar boundary.
AC3D8 elements, spherical boundary.
AC2D4 elements, oblique planar boundary.
AC2D4 elements, circular boundary.
AC3D4 elements, oblique planar boundary.
AC3D4 elements, spherical boundary.
AC2D3 elements, oblique planar boundary.
AC2D3 elements, circular boundary.
AC3D6 elements, oblique planar boundary.

ASI1 ASI2 ASI3
ASI2A ASI3A
ASI4 ASI8
AC1D2 AC1D3
AC2D4 AC2D8
ACAX4 ACAX8
For the ASI element tests the physical problem is similar to the nonreflective boundary test. Here, however, there is no volumetric drag, and a portion of the length of the body of air in the tube is modeled with truss elements. These are given Young's modulus and density to match the bulk modulus, ![]() 1.424 × 105 N/m2, and density,
1.424 × 105 N/m2, and density, ![]() 1.21 kg/m3, of air. The rest of the tube is modeled with acoustic elements that have the properties of air. Acoustic-structural coupling is set up between the structural region and the acoustic region using ASI elements, and a nonreflective end condition is applied.
1.21 kg/m3, of air. The rest of the tube is modeled with acoustic elements that have the properties of air. Acoustic-structural coupling is set up between the structural region and the acoustic region using ASI elements, and a nonreflective end condition is applied.
This problem is analyzed for the one-dimensional case using ASI1 elements, for the two-dimensional case using ASI2 and ASI3 elements, for the axisymmetric case using ASI2A and ASI3A elements, and for the three-dimensional case using ASI4 and ASI8 elements. All the nodes in these models are constrained such that they have only the horizontal translation degree of freedom to simulate one-dimensional wave propagation.
The results are within 1% of the analytical results, which are given as comments in the input files.
ASI1/AC1D2 elements.
ASI1/AC1D3 elements.
ASI2/AC2D4 elements.
ASI3/AC2D8 elements.
ASI2A/ACAX4 elements.
ASI3A/ACAX8 elements.
ASI4/AC3D8 elements.
ASI8/AC3D20 elements.

Tabular impedance properties on each of the acoustic infinite elements for transient and steady-state dynamic analyses in ABAQUS/Standard.
These tests compare the behavior of acoustic infinite elements with and without impedance conditions defined on the semi-infinite sides. In all models the acoustic infinite elements are coupled directly to structural elements using steel material properties. The acoustic infinite elements use air properties and an impedance condition on one semi-infinite side with a tabular value corresponding to one-half the material impedance. In the steady-state dynamic analyses the frequency is varied from 1 to 200 Hz. In the transient dynamic analyses the elements are excited using a sinusoidal amplitude with an angular frequency of 5.
The reductions in pressure amplitude due to the presence of the impedance condition on the acoustic infinite element sides are apparent in contour plots of the acoustic pressure.
ACIN2D2 and ACIN2D3 elements, semi-infinite side impedance.
ACIN2D2 and ACIN2D3 elements, semi-infinite side impedance.
ACIN3D3, ACIN3D4, ACIN3D6, and ACIN3D8 elements, semi-infinite side impedance.
ACIN3D3, ACIN3D4, ACIN3D6, and ACIN3D8 elements, semi-infinite side impedance.
ACINAX2 and ACINAX3 elements, semi-infinite side impedance.
ACINAX2 and ACINAX3 elements, semi-infinite side impedance.
ACIN2D2 elements, semi-infinite side impedance.
ACIN3D3 and ACIN3D4 elements, semi-infinite side impedance.
ACINAX4 elements, semi-infinite side impedance.