Products: ABAQUS/Standard ABAQUS/CAE
Contact pairs in ABAQUS/Standard:
can be used to define interactions between bodies in mechanical, coupled temperature-displacement, coupled pore pressure-displacement, coupled thermal-electrical, and heat transfer simulations;
are part of the model definition;
can be formed using a pair of rigid or deformable surfaces or, in two dimensions, a single deformable surface;
do not have to use surfaces with matching meshes;
cannot be formed using two rigid surfaces; and
cannot be formed with one two-dimensional surface and one three-dimensional surface.
ABAQUS/Standard defines contact between two bodies in terms of two surfaces that may interact; these surfaces are called a “contact pair.” ABAQUS/Standard defines “self-contact” in terms of a single surface.
The order in which the two surfaces are specified is critical because of the manner in which surface interactions are discretized. For each node on the “slave” surface ABAQUS/Standard attempts to find the closest point on the “master” surface of the contact pair where the master surface's normal passes through the node on the slave surface (see Figure 21.2.1–1). The interaction is then discretized between the point on the master surface and the slave node.
ABAQUS/Standard defines the contact conditions between two bodies using a strict “master-slave” algorithm. In mechanical contact problems when two bodies are tied together (see “Defining tied contact in ABAQUS/Standard,” Section 21.2.5) or when the surfaces are bonded together (see “Interaction of debonded surfaces,” Section 22.1.7), the surface interactions involve constraints between the two bodies. In mechanical problems:
Each potential contact condition is defined in terms of a “slave” node and a “master” surface.
The slave nodes are constrained not to penetrate into the master surface; however, the nodes of the master surface can, in principle, penetrate into the slave surface (see Figure 21.2.1–2).
The contact direction is always normal to the master surface.
Figure 21.2.1–2 Penetration of master surface nodes into the slave surface is possible with the strict master-slave contact algorithm.
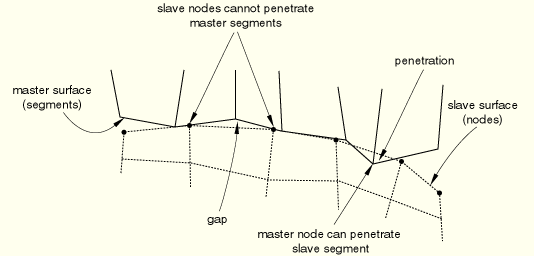
For self-contact each node on the surface becomes a “slave” node. “Master-slave” contact conditions can be established between each “slave” node and the surface. Hence, “slave” nodes and “master” segments can appear on either side.
Generally, contact interactions occur between two surfaces. However, in the strict master-slave contact formulation used in ABAQUS/Standard, only the master surface is used as a surface, where its geometry and orientation are taken into consideration. The only data that ABAQUS/Standard needs from the slave surface are the location of its nodes and the surface area associated with each node; the direction of the slave surface's normal is not relevant in strict master-slave contact. Thus, a slave surface can be defined as a group of nodes—a node-based surface.
Slave surfaces must always be attached to deformable bodies or deformable bodies defined as rigid. Analytical and rigid-element-based surfaces must always be the master surface in the contact pair. Both surfaces in a contact pair cannot be rigid surfaces with the exception of deformable surfaces defined as rigid. A node-based surface must always be the slave surface.
When both surfaces in a contact pair are deformable surfaces, you have to choose which surface will be the slave surface and which will be the master surface. Generally, the master surface should be chosen as the surface of the stiffer body or as the surface with the coarser mesh if the two surfaces are on structures with comparable stiffnesses. The stiffness of the structure and not just the material should be considered when choosing the master and slave surface. For example, a thin sheet of metal may be less stiff than a larger block of rubber even though the steel has a larger modulus than the rubber material. If the stiffness and mesh density are the same on both surfaces, the preferred choice is not always obvious.
When creating a surface that may be used as a master surface in a contact or interaction analysis, the contact algorithm in ABAQUS/Standard imposes the following restrictions on the master surface:
The master surface must be element-based or analytical.
The master surface must have the proper orientation.
The master surface must be continuous.
In finite-sliding mechanical contact simulations the master surface should be smoothed.
See “Defining element-based surfaces,” Section 2.3.2, “Defining node-based surfaces,” Section 2.3.3, and “Defining analytical rigid surfaces,” Section 2.3.4, for general restrictions on defining surfaces.
Edge-based surfaces (“Defining element-based surfaces,” Section 2.3.2) on three-dimensional shell elements cannot be used in a contact analysis.
A master surface must have a consistent orientation. The direction of the master surface's outward normal is critical for the proper detection of contact.
Except for initial interference fit problems, the slave surface should be on the same side of the master surface as the outward normal. If, in the initial configuration, it is not, ABAQUS/Standard will detect overclosure of the surfaces and may have difficulty finding an initial solution if the overclosure is severe. In most of these cases the analysis will immediately fail to converge. Figure 21.2.1–3 illustrates the proper and improper specification of the master surface's outward normal.
ABAQUS/Standard provides a detailed printout of the model's initial contact state during a data check analysis, which is useful in identifying incorrectly oriented master surfaces. It is easy to create a surface with the wrong orientation when using structural (beam and shell), membrane, truss, or rigid elements; therefore, check any surfaces created on these elements carefully.
A master surface cannot be made up of two or more disconnected regions—it must be continuous across element edges in three-dimensional models or through nodes in two-dimensional models. The continuity requirement has several implications for what constitutes a valid or invalid master surface definition. In two dimensions the surface must be either a simple, nonintersecting curve with two terminal ends or a closed loop. Figure 21.2.1–4 shows examples of valid and invalid two-dimensional surfaces.
In three dimensions an edge of an element face belonging to a valid surface may be either on the perimeter of the surface or shared by one other face. Two element faces forming a contact surface cannot be joined just at a shared node; they must be joined across a common element edge. An element edge cannot be shared by more than two surface facets. Figure 21.2.1–5 illustrates valid and invalid three-dimensional surfaces.
The continuity requirement applies to both automatically generated free surfaces and surfaces defined with element face identifiers (see “Defining element-based surfaces,” Section 2.3.2). Figure 21.2.1–6 shows an automatically generated free surface resulting from the specification of an element set consisting of two disjointed groups of elements. The resulting surface is not continuous since it is composed of two disjoint open curves. This surface could be used as a slave surface but would be invalid as a master surface.
The finite-sliding contact algorithm (“Contact formulation for ABAQUS/Standard contact pairs,” Section 21.2.2) performs best when there are no sharp corners on two-dimensional master surfaces and no sharp transitions of the normal vector on three-dimensional master surfaces. Convergence problems can occur if faceted master surfaces are used. Therefore, ABAQUS/Standard automatically smoothes all master surfaces in finite-sliding simulations. Smoothing of deformable master surfaces and rigid surfaces defined with rigid elements is discussed in “Contact formulation for ABAQUS/Standard contact pairs,” Section 21.2.2. Smoothing of analytical rigid surfaces is discussed in “Defining analytical rigid surfaces,” Section 2.3.4.
To define a contact pair, you must indicate which pairs of surfaces will interact with one another. The sequence in which you specify the surfaces depends on the nature of the surfaces being paired together.
When a contact pair contains two deformable surfaces, you must choose which surface will be the slave surface and which will be the master surface.
| Input File Usage: | *CONTACT PAIR slave_surface_name, master_surface_name |
| ABAQUS/CAE Usage: | Interaction module: Create Interaction: Surface-to-surface contact (Standard): select the master surface, click Surface, select the slave surface |
ABAQUS/Standard cannot use three-dimensional beams or trusses to form a master surface because the elements do not have enough information to create unique surface normals. However, these elements can be used to define a slave surface. Two-dimensional beams and trusses can be used to form both master and slave surfaces.
Edge-based surfaces on three-dimensional shells cannot be used in a contact pair definition. Such surfaces can be used only in coupling constraints (see “Coupling constraints,” Section 20.3.2) and shell-to-solid coupling constraints (see “Shell-to-solid coupling,” Section 20.3.3).
It is possible for master surface nodes to penetrate the slave surface with the strict master-slave algorithm used by ABAQUS/Standard, especially for soft bodies contacting each other under large contact pressures. Refining the slave surface mesh often minimizes the penetration of the master surface nodes. If the refinement technique does not work or is not practical, a symmetric master-slave method can be tried. To use this method, define two contact pairs using the same two surfaces, but switch the roles of master and slave surface for the two contact pairs.
This method causes ABAQUS/Standard to treat each surface as a master surface and, thus, involves additional computational expense because contact searches must be conducted twice for the same contact pair. The increased accuracy provided by this method must be compared to the additional computational cost.
Do not use symmetric master-slave contact pairs if the surfaces have matching meshes. The nodes on the surfaces will be overconstrained if node-to-node contact occurs. Such overconstrained nodes typically cause ABAQUS/Standard to report zero pivots.
When symmetric master-slave contact pairs are used in a finite-sliding simulation, it is possible that ABAQUS/Standard will report one of the surfaces as open and the other as closed. Typically this is caused by the shape or relative mesh refinement of the two surfaces. In two-dimensional finite-sliding problems smoothing of the master surface may also play a role.
It can be difficult to interpret the results from symmetric master-slave contact pairs. In single master-slave contact pairs the results are reported only for the slave surface. In symmetric master-slave contact pairs both surfaces are slave surfaces, so each has results associated with it. The problem is that the results for contact pressure are not independent of each other; the contact pressure on one surface will not necessarily be equivalent to the pressure on the other. The total contact pressure acting on both surfaces is the sum of the contact pressures on each side of the interface. Frictional slip is calculated independently for each surface based on the contact pressure for that surface and the friction coefficient. Limits on the frictional shear stress, such as the optional equivalent shear stress limit that you can specify for the friction model (see “Using the optional shear stress limit” in “Frictional behavior,” Section 22.1.4), may not be applied correctly because the contact pressure acting on each surface will be less than the contact pressure calculated with a single master-slave contact pair.
| Input File Usage: | *CONTACT PAIR surface_1, surface_2 surface_2, surface_1 |
| ABAQUS/CAE Usage: | Interaction module:
Create Interaction: Surface-to-surface contact (Standard): select the
master surface, click Surface, select the slave surface |
When modeling contact between a rigid surface and a deformable surface, the slave surface must be either the deformable surface or a rigid surface defined on a deformable body (see “Rigid body definition,” Section 2.4.1). Analytical rigid surfaces or rigid surfaces composed of rigid elements cannot be defined as the slave surface.
Define contact between a single surface and itself by specifying only a single surface or by specifying the same surface twice.
| Input File Usage: | Use either of the following options: |
*CONTACT PAIR surface_1, *CONTACT PAIR surface_1, surface_1 |
| ABAQUS/CAE Usage: | Interaction module: Create Interaction: Self-contact (Standard): select the surface or Surface-to-surface contact (Standard): select the surface, click Surface, select the surface again |
Self-contact is valid only for mechanical surface interactions and is limited to finite sliding with element-based surfaces.
Since a node of a self-contacting surface can be both a slave node and a member of the master surface, contact behavior is very similar to symmetric master-slave contact pairs. The characteristics described in the respective section above apply in this case. To avoid overconstraining, an exception is made in two dimensions when a surface folds onto itself forming a sharp corner; in that case the nodes adjacent to the vertex follow a strict master-slave algorithm. Three-dimensional self-contact can be activated only if penalty-type contact is used.
A node-based surface does not contain enough information for ABAQUS/Standard to form surface normals and, therefore, can be used only as the slave surface of a contact pair.
| Input File Usage: | *CONTACT PAIR node_based_surface_name, surface_name |
| ABAQUS/CAE Usage: | Interaction module: Create Interaction: Surface-to-surface contact (Standard): select the master surface, click Node Region, select the slave region |
Use node-based surfaces with caution when the contact property definition includes thermal or electrical interactions because the heat fluxes or electric currents between the surfaces may be calculated incorrectly unless the precise surface area is associated with each node. For details see “Thermal contact properties,” Section 22.2.1, or “Electrical contact properties,” Section 22.3.1.
If during an iteration a slave node is found to have penetrated the master surface by more than a specific distance (
), ABAQUS/Standard abandons the increment and tries again with a smaller increment size. The default value of is the radius of a sphere that circumscribes a characteristic surface element face. When calculating the default value, ABAQUS/Standard uses only the slave surface of the contact pair. The value of for each contact pair in the model is printed in the data (.dat) file. While the default value of should prove to be sufficient for the majority of contact simulations, in some cases it may be necessary to change the default value for a given contact pair. These cases include:
Models in which the master surface is highly curved. The default value of may sometimes lead to situations as shown in Figure 21.2.1–7. During the iterative solution process a slave node initially at point a may move to point b, penetrating the master surface with overclosure h less than . ABAQUS/Standard may attempt to move the slave node to point c on the master surface. To avoid this situation, specify a smaller value for to force ABAQUS/Standard to abandon the increment and to try a smaller increment size.
Models in which ABAQUS/Standard cannot calculate a reasonable because a node-based surface is used. If there are other contact pairs in the model with surfaces, ABAQUS/Standard uses the average dimension of all of the slave surface element faces. If there are no other contact pairs, ABAQUS/Standard uses a characteristic element dimension of the entire model.
Models in which the contact face dimensions in a slave surface vary greatly.
Models in which the slave surface mesh is very refined compared with the typical surface dimensions so that overclosures much larger than the default can be resolved easily.
Models in which contact pairs with softened contact allow significant penetration (see “Contact pressure-overclosure relationships,” Section 22.1.2).
| Input File Usage: | Use the following option to specify a nondefault value of : |
*CONTACT PAIR, HCRIT= |
| ABAQUS/CAE Usage: | You cannot change the default value of in ABAQUS/CAE. |
Second-order elements not only provide higher accuracy but also capture stress concentrations more effectively and are better for modeling geometric features than first-order elements. However, some of the second-order elements may not be suited for contact simulations with the default “hard” contact relationship or for analyses requiring large element distortions.
Some second-order elements can be problematic in contact simulations with the default “hard” contact relationship because of the distribution of equivalent nodal forces when a pressure acts on the face of the element. As shown in Figure 21.2.1–8, a constant pressure applied to the face of a second-order element, which does not have a midface node, produces forces at the corner nodes acting in the opposite sense of the pressure.
Figure 21.2.1–8 Equivalent nodal loads produced by a constant pressure on the second-order element face in “hard” contact simulations.
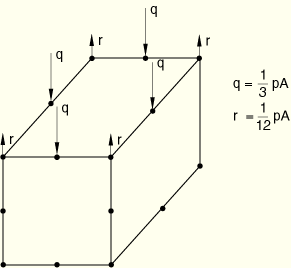
The element families C3D20(RH), C3D15(H), S8R5, and M3D8 are converted to the families C3D27(RH), C3D15V(H), S9R5, and M3D9, respectively. Since ABAQUS/Standard does not convert second-order coupled temperature-displacement and coupled pore pressure–displacement elements, penalty-type contact constraint enforcement should be used (see “Contact pressure-overclosure relationships,” Section 22.1.2).
The modified second-order tetrahedral elements (C3D10M) in ABAQUS/Standard are designed to be used in complex “hard” contact simulations. Regular second-order tetrahedral elements (C3D10) have zero contact force at their corner nodes, leading to poor predictions of the contact pressures. They should, therefore, not be used in “hard” contact problems. The modified second-order tetrahedral elements can calculate the contact pressures accurately.
Second-order elements can be used in contact simulations with the penalty-type contact constraint enforcement to yield better stresses at the contact interface. The regular tetrahedral elements may not perform well in analyses involving impact or nearly incompressible material response, such as in problems with a large amount of plastic deformation. The modified second-order tetrahedral elements should be used in these circumstances.
Every contact pair in a model must refer to a contact property definition, even if the contact pair uses the default contact property models. See “Mechanical contact properties: overview,” Section 22.1.1, for information on defining contact properties.
Multiple contact pairs can refer to the same contact property definition.
| Input File Usage: | Use both of the following options: |
*CONTACT PAIR, INTERACTION=interaction_property_name surface_1, surface_2 *SURFACE INTERACTION, NAME=interaction_property_name |
| ABAQUS/CAE Usage: | Interaction module: |
Create Interaction Property: Name: interaction_property_name, Contact Interaction editor: Contact interaction property: interaction_property_name |
Figure 21.2.1–9 shows the mesh used in this example. For purposes of this example, the surface ASURF is the slave surface of the contact pair. The property definition for the contact pair (GRATING) uses the finite-sliding formulation with a friction model where 
=0.4 and the default “hard” contact model for the behavior normal to the surfaces.
*HEADING … *SURFACE, NAME=ASURF ESETA, *SURFACE, NAME=BSURF ESETB, *CONTACT PAIR, INTERACTION=GRATING ASURF, BSURF *SURFACE INTERACTION, NAME=GRATING *FRICTION 0.4 *NSET, NSET=SNODES 101, 102, 103 *STEP, NLGEOM … *END STEP
You can write the contact surface variables associated with the interaction of contact pairs to the ABAQUS/Standard data (.dat), results (.fil), and output database (.odb) files. All contact pair results are given at the nodes of the slave surface.
You can:
request output associated with a given contact pair;
request output associated with a given slave surface, including contributions from all of the contact pairs to which the slave surface belongs; and
limit the output by specifying a node set containing a subset of the nodes on the slave surface.
For small-sliding contact problems the contact area is calculated in the input file preprocessor from the undeformed shape of the model; thus, it does not change throughout the analysis. Contact pressures for small-sliding contact are calculated according to the invariant contact area. This behavior is different from that in finite-sliding contact problems, where the contact area and contact pressures are calculated according to the deformed shape of the model.
In an axisymmetric analysis the total forces and moments transmitted between the contacting bodies as a result of contact pressure and frictional stress are computed in the same manner as in a two-dimensional analysis. As a result, the component of the total forces along the 
-axis is nonzero, and the components of the total moments include contributions from the total forces along the -axis.
The following input could be used for the example contact definition given above to request the default printed output for only the slave nodes 101, 102, and 103:
*CONTACT PRINT, SLAVE=ASURF, MASTER=BSURF, NSET=SNODESThis output request creates a table of output variables in the printed data (.dat) file. Each row of the table corresponds to a slave node in node set SNODES. The first column of the table identifies the slave node for that row. Because this is a mechanical contact simulation, the second column specifies the contact status at the slave node. Since the contact property definition includes frictional properties, the contact status may be open (OP), closed and sticking tangentially (ST), or closed and sliding tangentially (SL). The remaining columns contain the surface variables requested. In this example the default variables—contact pressure, contact opening, frictional shear stress, and relative tangential slip—were requested. This output request produces the following table in the data file:
CONTACT OUTPUT FOR SLAVE SURFACE ASURF AND MASTER SURFACE BSURF
NODE STATUS CPRESS CSHEAR1 COPEN CSLIP1
101 OP 0. -4.5870E-14 0.66 -0.24
102 ST 6.59 -2.585 -3.3168E-14 -0.4598
103 SL 4.32 -1.73 -2.6276E-13 -0.9946The OP status indicates that the slave node is not in contact with the master surface. In the sample output above, node 101 is open and, consequently, the contact pressure variable CPRESS is zero. The COPEN variable reports that this node is 0.66 length units away from the master surface.
The ST status indicates that the slave node is in contact with the master surface and is “sticking.” The frictional shear stress acting at the node is below the critical shear stress 
, where 
is the value of contact pressure shown under CPRESS. In the sample output above, node 102 is sticking since the frictional shear stress CSHEAR1 is below the critical value of 2.64 (0.4 × 6.59). The CSLIP1 variable is the total accumulated (integrated) slip at the slave node. The negative magnitude of CSLIP1 indicates that the node has moved in the negative first slip direction on BSURF. For details on how the slip directions are defined, see “Contact formulation for ABAQUS/Standard contact pairs,” Section 21.2.2. The accumulated slip is the sum of each increment of slip during the analysis.
The SL status indicates that the slave node is in contact with the master surface and it is sliding—the frictional shear stress is at the critical shear stress 
=
=
. In the sample output above, node 103 is sliding, and the frictional shear stress CSHEAR1 is equal to the friction limit 1.73 (0.4 × 4.32).
In the absence of frictional properties when a slave node is in contact with the master surface, its status reads CL for “closed.”
In this example, additional output variables can also be requested by using the following option:
*CONTACT PRINT, SLAVE=ASURF, MASTER=BSURF, NSET=SNODES CFN,CFS,CAREA CMN,CMS CFT,CMT XN,XS,XT
Such an output request creates four additional tables of output variables in the printed data (.dat) file. These tables summarize the total forces and moments transmitted between the contacting bodies as a result of contact pressure and frictional stress, the total contact area, and the coordinates of the centers of the contact and frictional forces. The content of each table is given below:
CONTACT OUTPUT FOR SLAVE SURFACE ASURF AND MASTER SURFACE BSURF CFNM CFN1 CFN2 CFN3 CFSM CFS1 CFS2 CFS3 CAREA 0.608 0.10 0.60 0 0.104 0.10 0.03 0 3.11 CONTACT OUTPUT FOR SLAVE SURFACE ASURF AND MASTER SURFACE BSURF CMNM CMN1 CMN2 CMN3 CMSM CMS1 CMS2 CMS3 0.01 0 0 0.01 0.002 0 0 0.002 CONTACT OUTPUT FOR SLAVE SURFACE ASURF AND MASTER SURFACE BSURF CFTM CFT1 CFT2 CFT3 CMTM CMT1 CMT2 CMT3 0.66 0.20 0.63 0 0.012 0 0 0.012 CONTACT OUTPUT FOR SLAVE SURFACE ASURF AND MASTER SURFACE BSURF XN1 XN2 XN3 XS1 XS2 XS3 XT1 XT2 XT3 0.1 0 0 0.01 0.02 0 0.11 0.02 0
When modeling surface-based contact with axisymmetric elements (type CAX and CGAX elements), ABAQUS/Standard can calculate the maximum torque (output variable CTRQ) that can be transmitted about the 
-axis. This capability is often of interest when modeling threaded connectors (see “Axisymmetric analysis of a threaded connection,” Section 1.1.19 of the ABAQUS Example Problems Manual). The maximum torque, 
, is defined as
is the pressure transmitted across the interface, is the radius to a point on the interface, and 
is the current distance along the interface in the – plane. This definition of “torque” effectively assumes a friction coefficient of unity.