Product: ABAQUS/Standard
The inelastic constitutive theory provided in ABAQUS/Standard for modeling cohesionless materials is based on the critical state plasticity theory developed by Roscoe and his colleagues at Cambridge (Schofield et al., 1968, and Parry, 1972). The specific model implemented is an extension of the “modified Cam-clay” theory. The discussion is entirely in terms of effective stress: the soil may be saturated with a permeating fluid that carries a pressure stress and is assumed to flow according to Darcy's law. The continuum theory of this two phase material is described in “Continuity statement for the wetting liquid phase in a porous medium,” Section 2.8.4.
The modified Cam-clay theory is a classical plasticity model. It uses a strain rate decomposition in which the rate of mechanical deformation of the soil is decomposed into an elastic and a plastic part; an elasticity theory; a yield surface; a flow rule; and a hardening rule. These various parts of the theory are defined in this section. The model is implemented numerically using backward Euler integration of the flow rule and hardening rule: this approach is used throughout ABAQUS for plasticity models.
The basic ideas of the Cam-clay model are shown geometrically in Figure 4.4.3–1 to Figure 4.4.3–7. The main features of the model are the use of an elastic model (either linear elasticity or the porous elasticity model, which exhibits an increasing bulk elastic stiffness as the material undergoes compression) and for the inelastic part of the deformation a particular form of yield surface with associated flow and a hardening rule that allows the yield surface to grow or shrink.
A key feature of the model is the hardening/softening concept, which is developed around the introduction of a “critical state” surface: the locus of effective stress states where unrestricted, purely deviatoric, plastic flow of the soil skeleton occurs under constant effective stress. This critical state surface is assumed to be a cone in the space of principal effective stress (Figure 4.4.3–1), whose vertex is the origin (zero effective stress) and whose axis is the equivalent pressure stress, 
.
-plane (the plane in principal stress space orthogonal to the equivalent pressure stress axis) is circular in the original form of the critical state model: in ABAQUS this has been extended to the more general shape shown in Figure 4.4.2–2. In the section of effective stress space defined by the equivalent pressure stress——and a measure of equivalent deviatoric stress—
(the definition of is given later in this section)—the critical state surface appears as a straight line, passing through the origin, with slope 
(see Figure 4.4.3–2 and Figure 4.4.3–3). The modified Cam-clay yield surface has the same shape in the -plane as the critical state surface, but in the – plane it is assumed to be made up of two elliptic arcs: one arc passes through the origin with its tangent at right angles to the pressure stress axis and intersects the critical state line where its tangent is parallel to the pressure stress axis, while the other arc is a smooth continuation of the first arc through the critical state line and intersects the pressure stress axis at some nonzero value of pressure stress, again with its tangent at right angles to that axis (see Figure 4.4.3–4). Plastic flow is assumed to occur normal to this surface.The hardening/softening assumption controls the size of the yield surface in effective stress space. The hardening/softening is assumed to depend only on the volumetric plastic strain component and is such that, when the volumetric plastic strain is compressive (that is, when the soil skeleton is compacted), the yield surface grows in size, while inelastic increase in the volume of the soil skeleton causes the yield surface to shrink. The choice of elliptical arcs for the yield surface in the (
) plane, together with the associated flow assumption, thus causes softening of the material for yielding states where 
(to the left of the critical state line in Figure 4.4.3–2, the “dry” side of critical state) and hardening of the material for yielding states where 
(to the right of the critical state line in Figure 4.4.3–3, the “wet” side of critical state).
The preceding discussion describes the concepts of the theory. These are now formalized, as they are implemented in ABAQUS/Standard.
The volume change is decomposed as
where
is the ratio of current volume to original volume, 
is the ratio of current to original volume of the soil grain particles, 
is the elastic (recoverable) part of the ratio of current to original volume of the soil volume, and 
is the plastic (nonrecoverable) part of the ratio of current to original volume of the soil volume.Volumetric strains are defined as
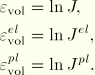
These definitions and Equation 4.4.3–1 result in the usual additive strain rate decomposition for volumetric strain rates:
The model also assumes the deviatoric strain rates decompose in an additive manner, so that the total strain rates decompose as
is a unit matrix.The elastic behavior can be modeled as linear or by using the porous elasticity model, typically with a zero tensile strength, as described in “Porous elasticity,” Section 4.4.1.
The modified Cam-clay yield function is defined in terms of the equivalent effective pressure stress, , and the Mises equivalent stress and third stress invariant, defined as
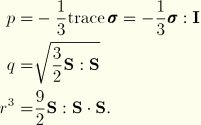
The surface is
In this equation 
is a user-specified constant that can be a function of temperature 
and other predefined field variables 
. This constant is used to modify the shape of the yield surface on the “wet” side of critical state, so the elliptic arc on the “wet” side of critical state has a different curvature from the elliptic arc used on the “dry” side: 
on the “dry” side of critical state, while 
in most cases on the “wet” side, as shown in Figure 4.4.3–4. 
defines the hardening of the plasticity model, and is the point on the -axis at which the elliptic arcs of the yield surface intersect the critical state line, as indicated in Figure 4.4.3–4. 
is the slope of the critical state line in the – plane (the ratio of to at critical state); and 
, where 
is used to shape the yield surface in the plane, and is defined as
is a user-defined constant. If 
, the yield surface does not depend on the third stress invariant, and the -plane section of the yield surface is a circle: this choice gives the original form of the Cam-clay model. The effect of different values of 
on the shape of the yield surface in the -plane is shown in Figure 4.4.2–2. To ensure convexity of the yield surface, 
.Associated flow is used with the modified Cam-clay plasticity model. The size of the yield surface is defined by 
: the evolution of this variable, therefore, characterizes the hardening or softening of the material. It is observed experimentally that, during plastic deformation,
is a constant. Integrating this equation, and using Equation 4.4.3–1, Equation 4.4.1–2, and Equation 4.4.1–4, we obtainwhere 
defines the position of at the beginning of the analysis—the initial overconsolidation of the material. The value of can be specified directly by the user or can be computed as
is the initial value of the equivalent pressure stress, and 
is the intercept of the virgin consolidation line with the void ratio axis in a plot of void ratio versus equivalent pressure stress, shown in Figure 4.4.3–6.The evolution of the yield surface can alternatively be defined as a piecewise linear function relating the yield stress in hydrostatic compression, 
, and the corresponding volumetric plastic strain 
(Figure 4.4.3–7):
, is then given by 
is the position on this axis corresponding to the initial state of the material, thus defining the initial hydrostatic pressure, 
and, hence, the initial yield surface size, .ABAQUS checks that the initial effective stress state lies inside or on the initial yield surface. At any material point where the yield function is violated, is adjusted so that Equation 4.4.3–3 is satisfied exactly (and, hence, the initial stress state lies on the yield surface).
).
).
plane.
