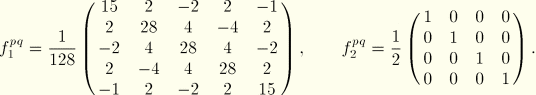3.6.7 Axisymmetric shell element allowing asymmetric loading

The ABAQUS/Standard element library includes a family of nonlinear thin shell elements with axisymmetric reference geometry that allow asymmetric loading and deformation (SAXA1N and SAXA2N). This section provides their theoretical formulation. These elements encompass a broad range of practical applications from the bending/ovalization of variable diameter pipes to the bending of circular plates. The theoretical formulation of these elements is similar to the general finite-strain shell element described in “Finite-strain shell element formulation,” Section 3.6.5. Furthermore, this formulation is the shell counterpart to the continuum axisymmetric bending elements described in “Axisymmetric elements allowing nonlinear bending,” Section 3.2.9.
As with the continuum axisymmetric bending formulation, the restriction is made that a plane of symmetry exists in the  –
– plane at
plane at 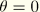 . Hence in-plane bending of the model is permitted, while deformations such as torsion about the axis of symmetry are precluded. The symmetries of the undeformed configuration and of the deformation are exploited through the assumption of particular displacement and rotation interpolations around the circumference of the shell. Specifically, Fourier series expansions are used in the
. Hence in-plane bending of the model is permitted, while deformations such as torsion about the axis of symmetry are precluded. The symmetries of the undeformed configuration and of the deformation are exploited through the assumption of particular displacement and rotation interpolations around the circumference of the shell. Specifically, Fourier series expansions are used in the  or circumferential direction that preserve the plane of symmetry.
or circumferential direction that preserve the plane of symmetry.
Geometric description

Let  be coordinate functions parametrizing the reference surface of the shell and let
be coordinate functions parametrizing the reference surface of the shell and let 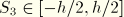 be the coordinate function in the thickness direction, where
be the coordinate function in the thickness direction, where 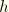 is the shell's initial thickness. (For a detailed account of the geometric description of the finite-strain shell formulation, see “Finite-strain shell element formulation,” Section 3.6.5.) Then points in the reference or undeformed configuration are identified by the normal coordinates mapping
is the shell's initial thickness. (For a detailed account of the geometric description of the finite-strain shell formulation, see “Finite-strain shell element formulation,” Section 3.6.5.) Then points in the reference or undeformed configuration are identified by the normal coordinates mapping
where

is the three-dimensional position of a material point,
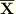
is the shell reference surface mapping, and
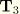
is the unit normal to the shell reference surface. The fact that
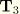
is a unit vector assumes that the reference configuration is (locally) of constant thickness. Owing to the axisymmetric reference configuration,
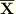
can be given relative to a global Cartesian coordinate system as
where
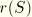
is the radius,
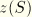
is the axial position, and
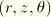
are the cylindrical coordinates. (Note that the usual convention for cylindrical coordinates
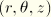
has been changed, which is consistent with the axisymmetric shell elements and the axisymmetric elements allowing nonlinear bending.) By definition the normal field to the shell reference surface is
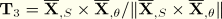
, which by direct computation yields
where
and
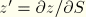
. Relative to the cylindrical coordinate system,
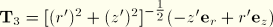
.
The basic kinematic assumption is that for any deformed configuration, the position of a point in the body can be identified by
where
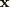
is the deformed position of the material point,
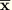
is the deformed shell reference surface mapping,
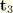
is the deformed unit director field, and
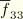
is the thickness change parameter. Of critical importance for any shell formulation is the treatment of the rotation field; that is, the treatment of the director field
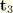
. The geometric description and the incremental update procedure for the director field are given in detail below.
Under the kinematic assumption above, the deformed configuration of the shell is completely determined by the reference surface mapping 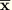 , the deformed director field
, the deformed director field 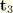 and the thickness parameter
and the thickness parameter 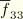 .
.
We define the following displacement quantities. Since 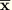 is an element of a (linear) vector space, we can define the reference surface displacement vector
is an element of a (linear) vector space, we can define the reference surface displacement vector  by the difference between the deformed reference surface and the undeformed reference surface; i.e.,
by the difference between the deformed reference surface and the undeformed reference surface; i.e.,
The director field, however, is a unit vector field that is not a member of a linear vector space. The orientation of the director field is defined in terms of a rotation vector
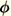
as
Here
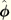
is the skew-symmetric matrix with axial vector
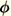
, defined by the properties
and
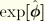
is an orthogonal transformation given by the closed-form expression
Alternatively, quaternion algebra can be used to specify the orientation of the deformed director field
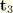
. In this case the orthogonal matrix
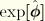
is replaced by the quaternion parameter
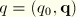
, where
The orientation of the unit director field then follows as
Similarly, the orthogonal transformation
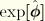
can be extracted from the quaternion parameter as
Interpolations

Displacement and rotation components are given relative to the cylindrical coordinate system 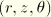 with orthonormal basis vectors
with orthonormal basis vectors 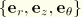 that are fixed in the reference or undeformed configuration. A general interpolation scheme for
that are fixed in the reference or undeformed configuration. A general interpolation scheme for 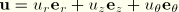 and
and 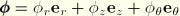 using a Fourier expansion in the
using a Fourier expansion in the 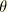 variable is
variable is
Here
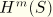
are the polynomial interpolation functions along the generator lines of the axisymmetric reference configuration;
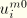
,
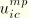
,
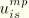
,
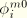
,
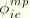
,
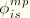
are the solution amplitude values (Fourier coefficients);
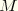
is the number of terms used in the interpolation along the generator lines; and
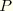
is the number of Fourier interpolation terms used around the circumference of the reference shell. Note that an axisymmetric deformation is obtained for the choice
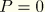
.
The symmetry requirement in the  –
– plane at
plane at 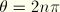 ,
, 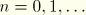 , eliminates many of the above Fourier coefficients. For the displacement vector the only admissible terms are
, eliminates many of the above Fourier coefficients. For the displacement vector the only admissible terms are
For the rotation components, symmetry requirements switch the role of the

and

components with the
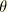
components:
For practical reasons the values of
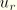
,
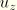
, and
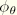
are often required at specific locations around the circumference of the shell. Therefore, displacement and rotation components
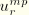
,
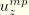
, and
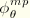
are used instead of the Fourier coefficients
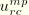
,
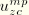
, and
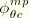
. Furthermore, a negative sign is introduced in the interpolation for
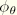
for the following reason: The ABAQUS convention for axisymmetric shell elements is that the axial tangent direction is drawn between nodes in ascending node number (the shell local 1-direction). The normal to the shell is then obtained by a 90° counter-clockwise rotation of the tangent (the shell local 3-direction). However, a positive rotation of the normal field (about the shell local 2-direction) is counterclockwise. This convention implies a left-handed shell local coordinate system. For the axisymmetric shell bending elements, a right-handed shell local coordinate system is required at the integration points; thus, the direction of positive rotation is reversed there.
Rearranging the Fourier series expansions and making the substitution 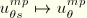 , the interpolations for the displacement components are
, the interpolations for the displacement components are
Similarly, replacing
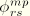
and
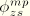
with
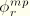
and
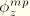
respectively, the interpolation for the rotation components becomes
In the above interpolations,
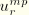
,
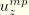
, and
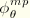
are physical displacement and rotation components at
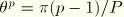
and
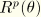
are trigonometric interpolation functions with the property that
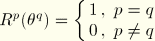
defined by:
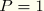 :
: 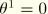 ,
, 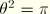 ,
,
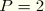 :
: 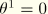 ,
, 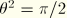 ,
, 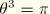 ,
,
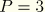 :
: 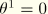 ,
, 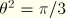 ,
, 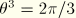 ,
, 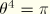 ,
,
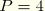 :
: 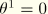 ,
, 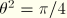 ,
, 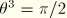 ,
, 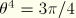 ,
, 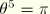 ,
,
As with the continuum axisymmetric bending element,
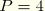
is the highest-order interpolation offered with respect to
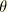
. The element becomes significantly more expensive as higher-order interpolations are used, and it is assumed that the general-purpose finite-strain shell is less expensive than using this element with
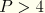
.
Virtual work

The virtual work expression from the three-dimensional theory is
where
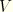
is the current volume of the deformed body,
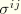
are the curvilinear components of the Cauchy stress tensor,
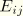
are the components of the Lagrange strain tensor, and
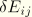
are the variational or linearized strain measure components. By definition the Lagrange strain tensor components are given by
Note that in the statement of virtual work, no choice has thus far been made regarding the curvilinear coordinate functions
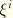
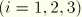
. Furthermore, the current volume measure
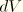
is given by the parametric relationship
We now introduce the kinematic assumption Equation 3.6.7–1 into the definition of 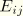 to find
to find
where differentiation is now with respect to the parametric coordinates, so that
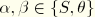
and
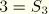
. Define the following shell strain measure components and kinematic relationships:
In the above,
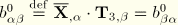
are the components of the second fundamental form of the undeformed reference surface.
Substituting the above definitions into the virtual work expression, we find (after some manipulation) that the volume integral reduces to the following integral over the deformed reference surface
where
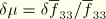
and the current reference surface Jacobian determinant is
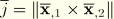
. In the above virtual work expression, the
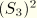
term in
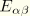
has been neglected. This term is
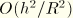
—where
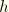
is the thickness and
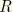
is some characteristic radius of curvature—and is negligible in light of the kinematic assumption
Equation 3.6.7–1. The shell stress resultant components are defined by the following integrals through the thickness of the shell:
For thin shells the Kirchhoff-Love approximation, which states that the deformed director field 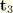 is (approximately) the normal field to the deformed reference surface, is introduced along with the plane stress assumption
is (approximately) the normal field to the deformed reference surface, is introduced along with the plane stress assumption 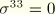 . Consistent with these approximations, we neglect all
. Consistent with these approximations, we neglect all 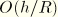 terms and terms proportional to the gradient of the thickness parameter. Accordingly, we set
terms and terms proportional to the gradient of the thickness parameter. Accordingly, we set
We can now summarize the virtual work expression for thin (Kirchhoff-Love) shells:
where the shell resultant components are defined in terms of the Cauchy stress tensor components by the integrals
In the expression for
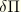
,
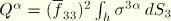
is interpreted as a constraint stress that enforces that the director field remain normal to the reference surface. Two other contributions to the virtual work expression
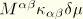
and
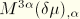
, where
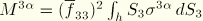
are
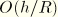
and, thus, neglected.
Orthonormal surface coordinate system and coordinate transformation

It is desirable to define stress resultant quantities relative to an orthonormal basis in the deformed configuration. To do this, we define a normal coordinate system 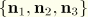 , where
, where 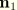 and
and 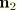 are tangent to the deformed reference surface and
are tangent to the deformed reference surface and 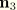 is the unit normal field.
is the unit normal field.
Define the following notation. Let 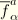
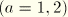 be the components of
be the components of 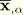 relative to the basis
relative to the basis 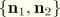 ; that is
; that is
Furthermore, let the inverse of the matrix of components
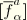
be given by
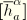
, such that
Note that the basis vectors
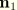
and
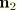
induce distance measuring coordinates
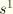
and
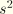
such that
It follows from
Equation 3.6.7–5 that the orthonormal tangent vectors are given by
For the material calculations, it is important to express both the strain and stress quantities relative to the local orthonormal frame 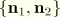 . Accordingly, let
. Accordingly, let 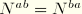 and
and 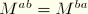 be the membrane and bending stress resultant components relative to this local orthonormal basis. Thus, we can write
be the membrane and bending stress resultant components relative to this local orthonormal basis. Thus, we can write
where we recall that
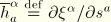
. Then the stress resultant contributions to the virtual work expression can be transformed as follows. First, the membrane contribution:
Recall, however, that by the definition of the coordinates
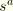
,
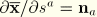
. Thus,
Similarly, the bending contribution is:
Let
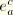
be the two-dimensional alternator, such that
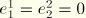
and
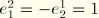
. Then
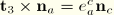
and
Since the second term in the brackets is proportional to the bending curvature, we neglect this term relative to the first, yielding
Strain displacement operators

We now write the virtual work expression Equation 3.6.7–4 in matrix operator notation. Define the following stress resultant component vectors:
Define the matrix strain displacement operators as follows:
where
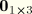
is the column of zeros
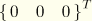
. Then the virtual work expression
Equation 3.6.7–4 is equivalently stated
Corotational coordinate system

Thus far 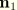 and
and 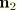 are any two orthonormal vectors in the tangent plane to the reference surface. We can uniquely choose these two vectors by requiring the matrix components of the incremental reference surface deformation gradient
are any two orthonormal vectors in the tangent plane to the reference surface. We can uniquely choose these two vectors by requiring the matrix components of the incremental reference surface deformation gradient 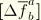 , where
, where
to be symmetric; i.e.,
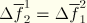
. Note that by definition
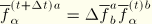
. This symmetry condition defines a corotational orthonormal basis in the deformed configuration. This orthonormal basis is calculated as follows.
Obtain the ABAQUS convention pair of orthonormal surface vectors 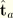 . We then rotate these vectors in the tangent plane to the reference surface about the normal vector
. We then rotate these vectors in the tangent plane to the reference surface about the normal vector 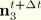 by the angle
by the angle 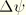 , where
, where 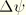 is determined by the symmetry condition
is determined by the symmetry condition 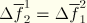 . Thus, we define
. Thus, we define
It follows by definition that
Therefore, define the quantity
The symmetry condition requires that
From this it can be determined that
and
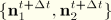
are then determined by
Equation 3.6.7–6.
Having determined the updated vectors 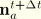 , we can calculate the quantities required for coordinate transformation. First the incremental deformation gradient components and the Jacobian matrix components:
, we can calculate the quantities required for coordinate transformation. First the incremental deformation gradient components and the Jacobian matrix components:
Note that due to the symmetry of the incremental deformation gradient components, there is no ambiguity in writing
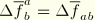
. We can now calculate the inverse components
Consistent linearization

The iterative solution procedure requires the calculation of the consistent tangent stiffness. This stiffness has two parts, one resulting from the material model and the other resulting from the changing geometry. We denote the second variational quantities with 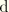 . Returning to Equation 3.6.7–4, the virtual work expression can be written as
. Returning to Equation 3.6.7–4, the virtual work expression can be written as
where
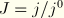
,
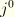
is the Jacobian determinant of the reference configuration parametrization given by
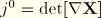
, and components are relative to the corotated frame with
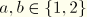
. We assume constitutive behavior such that
Thus, the variation of the virtual work expression yields
The first term in the integrand forms the material stiffness, while the second two terms form the geometric stiffness. The second variation of the strain measure components are calculated in
“Finite-strain shell element formulation,” Section 3.6.5. The second variation of the membrane strain is
The second variation of the bending strain is zero; i.e.,
Incremental degrees of freedom: interpolations and configuration updates

At the beginning of an increment we have the configuration at iteration 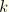 , denoted
, denoted 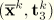 . In the incremental solution procedure we solve for the incremental displacement field and the incremental rotation field in components relative to the reference cylindrical coordinate system:
. In the incremental solution procedure we solve for the incremental displacement field and the incremental rotation field in components relative to the reference cylindrical coordinate system:
We use these incremental fields to update the configuration to iteration
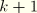
.
1. Reference surface update: The displacement increments are interpolated using the same interpolation scheme as the total displacement vector in Equation 3.6.7–2:
The reference surface position map is updated from the displacement increment by
2. Rotation field update: The incremental rotation field is updated with the same interpolation scheme as the total rotation field in Equation 3.6.7–3:
This incremental rotation vector corresponds to a finite rotation, characterized by quaternion parameters as
The total rotation quaternion parameter can be updated by the update formula
Similarly, the deformed unit director field can be updated from the incremental rotation field as
Here we have used the notation
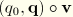
to denote the rotation of the vector
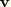
by the quaternion
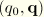
. The curvatures are calculated from the gradient of the director field, which is updated by
where
For completeness, we record the values of
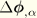
. First, along the generator lines we have
For the circumferential derivative we must account for the derivative of the basis vectors in the
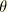
-direction:
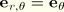
and

. Hence,
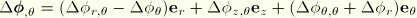
. Introducing the interpolation function, we have
where
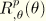
are computed from the definitions of the interpolation functions
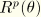
as given above and
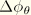
and
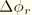
are given by the interpolation for the incremental rotation field as given in the Rotation Field Update.
Strain increment and stress resultant update

Following the formulation of the finite-strain shell element formulation in “Finite-strain shell element formulation,” Section 3.6.5, the three-dimensional (finite) strain increment is calculated as
Here the increment in the membrane strain components
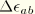
is given by the Hughes-Winget second-order approximation to the logarithmic membrane strain increment
and the increment in the bending strain components
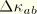
is given by the expression
where
As an example of the stress update procedure, consider the simple case of a Saint Venant-Kirchhoff material model. In this case,
where
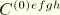
are the plane stress elastic coefficients given by
Note that
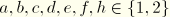
, and the components
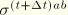
are relative to the current orthonormal basis
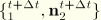
.
Pressure loads and load stiffness

For geometrically linear problems, equivalent nodal loads due to applied surface pressure are readily calculated since the geometry is axisymmetric. For geometrically nonlinear problems, however, asymmetric deformations must be taken into consideration.
The equivalent nodal loads associated with surface pressure  can be obtained by considering the virtual work contribution to the external loading
can be obtained by considering the virtual work contribution to the external loading
where
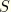
is the parametric surface coordinate in the
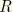
–
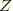
plane and the reference surface position is
with
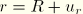
and
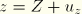
. Recall that the current position of a point can be expressed in terms of the axial interpolator
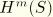
and the circumferential interpolators
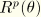
by
The terms in
Equation 3.6.7–7 can be worked out as follows:
and, hence,
The variations
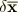
are written
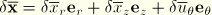
, where the components have interpolations similar to those in
Equation 3.6.7–7. Therefore, the virtual work contribution becomes
With the introduction of the interpolation functions, we obtain the equivalent nodal forces:
For geometrically linear analysis, the equivalent nodal forces reduce to the standard axisymmetric expressions
The linearization of the pressure loading term leads to the following pressure load stiffness matrix:
with
In the case of hydrostatic pressure ( dependent on
dependent on  ), additional terms must be included in the pressure load stiffness. These terms appear due to the variation of the pressure magnitude and are readily obtained from the expression
), additional terms must be included in the pressure load stiffness. These terms appear due to the variation of the pressure magnitude and are readily obtained from the expression
With use of the interpolation functions and denoting the additional contributions with an over-bar, we obtain the additional load stiffness contributions:
Penalty constraints: transverse shear and drill rotation

It is necessary to enforce rotation constraints at selected points on the element surface to prevent singular modes of deformation. One axial transverse shear constraint is enforced on the 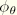 rotation field between each pair of nodes within each nodal plane. One circumferential transverse shear constraint and one drill rotation constraint on the rotation fields
rotation field between each pair of nodes within each nodal plane. One circumferential transverse shear constraint and one drill rotation constraint on the rotation fields 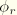 and
and 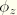 are enforced between each pair of nodes on a circumferential line of nodes. In each instance the rotation field is constrained to follow the nodal displacements. To summarize, for element SAXAMN:
are enforced between each pair of nodes on a circumferential line of nodes. In each instance the rotation field is constrained to follow the nodal displacements. To summarize, for element SAXAMN:
constraints are enforced, where
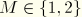
is the order of integration in the axial direction and
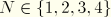
is the number of Fourier modes.
Transverse shear
The transverse shear strain is the measure of the amount the director field 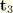 has rotated relative to the normal to the shell surface. We define the transverse shear strain as
has rotated relative to the normal to the shell surface. We define the transverse shear strain as
with no sum on

and force this quantity to be zero with a penalty constraint. Note that
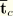
is a unit vector tangent to the shell surface defined by the displacement field along a parametric coordinate line. Recall that
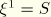
and

. Hence,
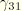
is the axial transverse shear strain and
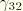
is the circumferential transverse shear strain.
For convenience, record the variation of the unit vector 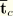 :
:
with no sum on

. Equivalently, the definition of
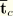
can be used to write
The linearized transverse shear strain is calculated as
Since by definition
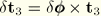
, it follows that
with no sum on

.
For completeness, the second variation of the transverse shear strain is
where terms proportional to
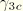
have been neglected and the coupling between
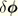
and
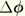
has been symmetrized.
Drill rotation
Mathematically, the equations governing the deformation of the shell are invariant with respect to drill rotations; that is, a rotation of the director field with axis of rotation parallel to the director. It is necessary then to assign a kinematic definition to this rotation. We define the drill strain as the difference between the rotation of the circumferential tangent vector as measured by the displacement field and that measured by the rotation field. Accordingly, we define the drill strain by
Here,

is the rotated reference axial tangent vector and
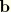
is the deformed (unit) circumferential tangent vector, defined by
In the above
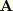
is a linear approximation to the axial tangent vector in the reference configuration given by
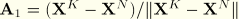
, where
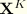
and
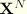
are the position vectors to two adjacent nodes in an axial plane. The drill rotation constraint then requires that the component of rotation about the normal to the surface match the in-plane rotation of the surface as measured by the displacement field.
The linearized drill strain calculation is similar to the transverse shear linearized strain calculation. Without repeating the calculation,
Similarly, the second variation of the drill strain
where terms proportional to
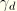
have been neglected and the coupling between
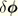
and
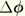
has been symmetrized.
Zero radius: collapsed edge

For the case when the reference radius of any point on the shell surface goes to zero, all of the offset nodes collapse to the same point and the edge constraints along that circumferential edge become redundant. It is, therefore, necessary to treat the zero radius case separately.
For the zero radius case all redundant degrees of freedom are constrained to follow the average motion of the nodes at 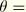 0° and
0° and 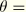 180°. The edge constraints are broken into two parts: First, a circumferential transverse shear strain is defined that requires that the rotation in the radial direction follow the circumferential rotations at the first and last nodal plane:
180°. The edge constraints are broken into two parts: First, a circumferential transverse shear strain is defined that requires that the rotation in the radial direction follow the circumferential rotations at the first and last nodal plane:
Introducing the interpolations, the linearized strain is
Note that
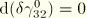
. Second, a drill rotation strain is defined that requires that the rotation about the
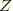
-axis be zero:
This leads to a linearized strain given by
Note that
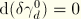
.
Mass matrix

At each material point the displacement components in the three directions (radial, axial, circumferential) are dependent only on the corresponding nodal displacement components. Hence, the mass matrix does not involve any coupling between the radial, axial, and circumferential degrees of freedom, and we can write the mass matrix in the form of three separate expressions:
Similarly, we can write the terms associated with the rotational degrees of freedom as:
Here the superscripts
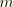
and

refer to a particular node in the

–

plane, and the superscripts

and
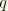
refer to a particular position along the circumference. The interpolation functions
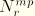
,
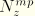
, and
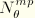
are the product of interpolation functions
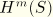
in the

–

plane and interpolation functions in the
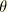
-direction:
The area integral used to form the mass matrix can be split then into an integral along the length of the element in the

–

plane and an integral around the circumference. For the

–

component of the mass matrix this yields
and for the
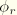
component of the mass matrix this yields:
The matrix can be written in a convenient form by defining the primitive mass matrix as
or for the rotational components as
These primitive mass matrices are the same mass matrices that are used for the regular axisymmetric shell elements. We can also define the circumferential distribution matrices
The various components of the mass matrix then take the form
The circumferential distribution matrices can be evaluated for various values of the number of terms 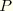 in the Fourier series. After some calculations the following results are obtained:
in the Fourier series. After some calculations the following results are obtained:
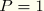 :
:
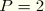 :
:
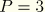 :
:
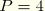 :
:

![]() –
–![]() plane at
plane at ![]() . Hence in-plane bending of the model is permitted, while deformations such as torsion about the axis of symmetry are precluded. The symmetries of the undeformed configuration and of the deformation are exploited through the assumption of particular displacement and rotation interpolations around the circumference of the shell. Specifically, Fourier series expansions are used in the
. Hence in-plane bending of the model is permitted, while deformations such as torsion about the axis of symmetry are precluded. The symmetries of the undeformed configuration and of the deformation are exploited through the assumption of particular displacement and rotation interpolations around the circumference of the shell. Specifically, Fourier series expansions are used in the ![]() or circumferential direction that preserve the plane of symmetry.
or circumferential direction that preserve the plane of symmetry.
![]() be coordinate functions parametrizing the reference surface of the shell and let
be coordinate functions parametrizing the reference surface of the shell and let ![]() be the coordinate function in the thickness direction, where
be the coordinate function in the thickness direction, where ![]() is the shell's initial thickness. (For a detailed account of the geometric description of the finite-strain shell formulation, see “Finite-strain shell element formulation,” Section 3.6.5.) Then points in the reference or undeformed configuration are identified by the normal coordinates mapping
is the shell's initial thickness. (For a detailed account of the geometric description of the finite-strain shell formulation, see “Finite-strain shell element formulation,” Section 3.6.5.) Then points in the reference or undeformed configuration are identified by the normal coordinates mapping ![]()
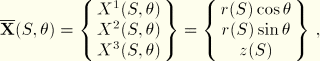
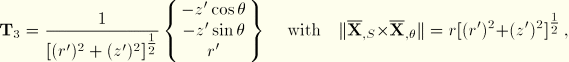
![]() , the deformed director field
, the deformed director field ![]() and the thickness parameter
and the thickness parameter ![]() .
.![]() is an element of a (linear) vector space, we can define the reference surface displacement vector
is an element of a (linear) vector space, we can define the reference surface displacement vector ![]() by the difference between the deformed reference surface and the undeformed reference surface; i.e.,
by the difference between the deformed reference surface and the undeformed reference surface; i.e., ![]()
![]()
![]()
![]()
![]()
![]()
![]()

![]() with orthonormal basis vectors
with orthonormal basis vectors ![]() that are fixed in the reference or undeformed configuration. A general interpolation scheme for
that are fixed in the reference or undeformed configuration. A general interpolation scheme for ![]() and
and ![]() using a Fourier expansion in the
using a Fourier expansion in the ![]() variable is
variable is 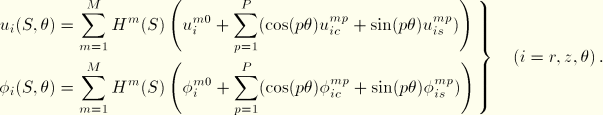
![]() –
–![]() plane at
plane at ![]() ,
, ![]() , eliminates many of the above Fourier coefficients. For the displacement vector the only admissible terms are
, eliminates many of the above Fourier coefficients. For the displacement vector the only admissible terms are 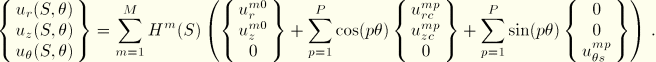
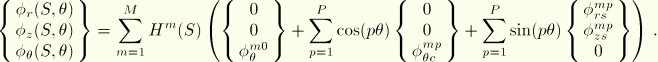
![]() , the interpolations for the displacement components are
, the interpolations for the displacement components are ![]() :
: ![]() ,
, ![]() ,
,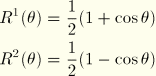
![]() :
: ![]() ,
, ![]() ,
, ![]() ,
,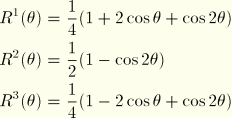
![]() :
: ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
,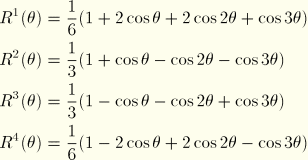
![]() :
: ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
,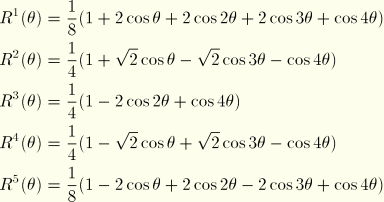

![]()
![]()
![]()
![]() to find
to find 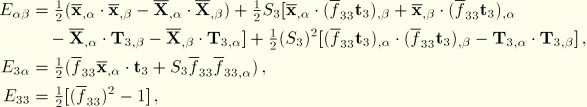
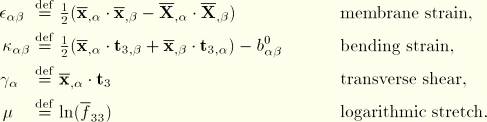
![]()
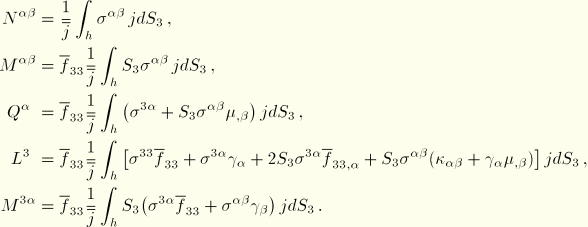
![]() is (approximately) the normal field to the deformed reference surface, is introduced along with the plane stress assumption
is (approximately) the normal field to the deformed reference surface, is introduced along with the plane stress assumption ![]() . Consistent with these approximations, we neglect all
. Consistent with these approximations, we neglect all ![]() terms and terms proportional to the gradient of the thickness parameter. Accordingly, we set
terms and terms proportional to the gradient of the thickness parameter. Accordingly, we set ![]()
![]()

![]() , where
, where ![]() and
and ![]() are tangent to the deformed reference surface and
are tangent to the deformed reference surface and ![]() is the unit normal field.
is the unit normal field.![]()
![]() be the components of
be the components of ![]() relative to the basis
relative to the basis ![]() ; that is
; that is ![]()
![]()
![]()
![]() . Accordingly, let
. Accordingly, let ![]() and
and ![]() be the membrane and bending stress resultant components relative to this local orthonormal basis. Thus, we can write
be the membrane and bending stress resultant components relative to this local orthonormal basis. Thus, we can write ![]()
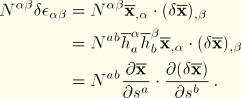
![]()
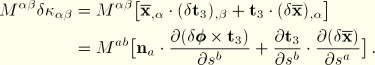
![]()
![]()

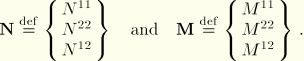
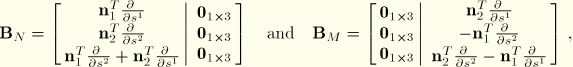
![]()

![]() and
and ![]() are any two orthonormal vectors in the tangent plane to the reference surface. We can uniquely choose these two vectors by requiring the matrix components of the incremental reference surface deformation gradient
are any two orthonormal vectors in the tangent plane to the reference surface. We can uniquely choose these two vectors by requiring the matrix components of the incremental reference surface deformation gradient ![]() , where
, where ![]()
![]() . We then rotate these vectors in the tangent plane to the reference surface about the normal vector
. We then rotate these vectors in the tangent plane to the reference surface about the normal vector ![]() by the angle
by the angle ![]() , where
, where ![]() is determined by the symmetry condition
is determined by the symmetry condition ![]() . Thus, we define
. Thus, we define ![]()
![]()
![]()
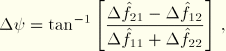
![]() , we can calculate the quantities required for coordinate transformation. First the incremental deformation gradient components and the Jacobian matrix components:
, we can calculate the quantities required for coordinate transformation. First the incremental deformation gradient components and the Jacobian matrix components: ![]()
![]()

![]() . Returning to Equation 3.6.7–4, the virtual work expression can be written as
. Returning to Equation 3.6.7–4, the virtual work expression can be written as ![]()
![]()
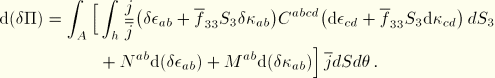
![]()
![]()

![]() , denoted
, denoted ![]() . In the incremental solution procedure we solve for the incremental displacement field and the incremental rotation field in components relative to the reference cylindrical coordinate system:
. In the incremental solution procedure we solve for the incremental displacement field and the incremental rotation field in components relative to the reference cylindrical coordinate system: ![]()
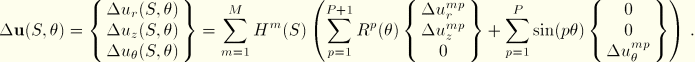
![]()
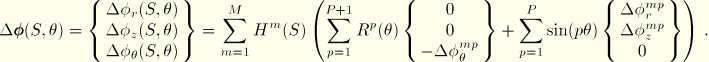
![]()
![]()
![]()
![]()
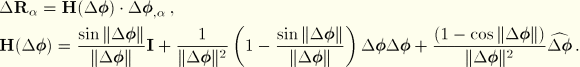
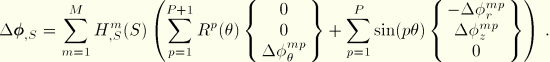
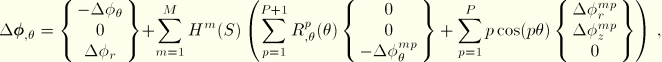

![]()
![]()
![]()
![]()
![]()
![]()

![]() can be obtained by considering the virtual work contribution to the external loading
can be obtained by considering the virtual work contribution to the external loading![]()
![]()
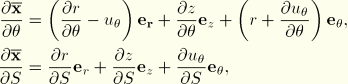
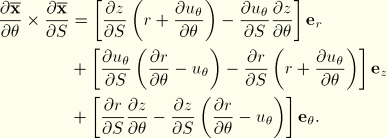
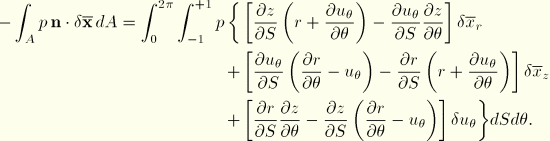
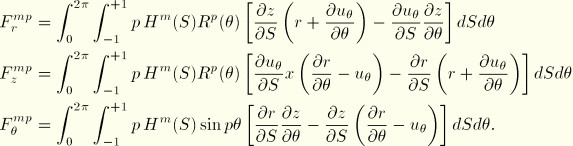
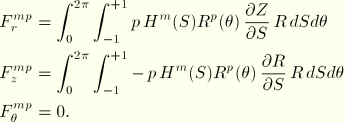
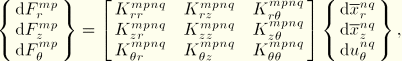
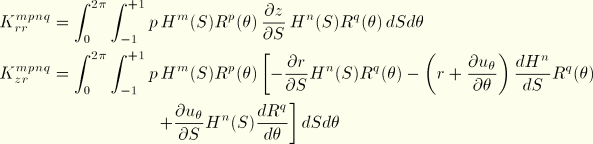
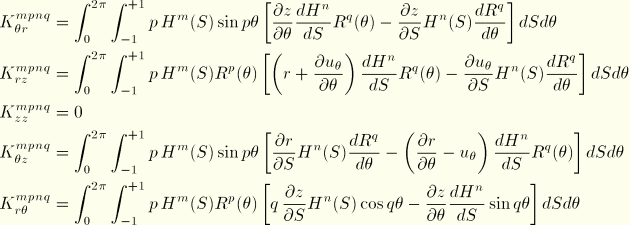
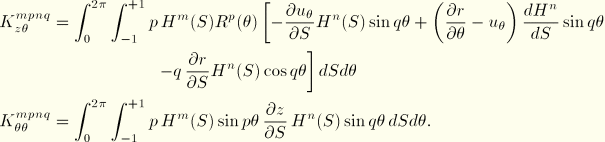
![]() dependent on
dependent on ![]() ), additional terms must be included in the pressure load stiffness. These terms appear due to the variation of the pressure magnitude and are readily obtained from the expression
), additional terms must be included in the pressure load stiffness. These terms appear due to the variation of the pressure magnitude and are readily obtained from the expression 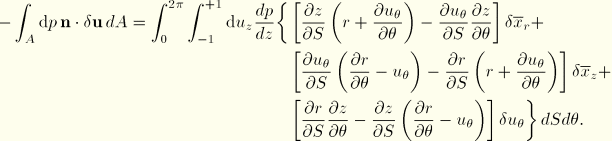
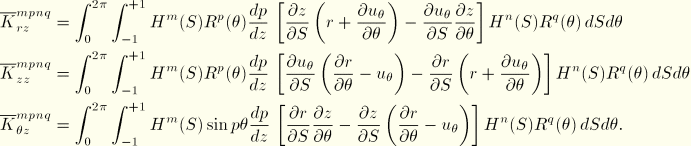

![]() rotation field between each pair of nodes within each nodal plane. One circumferential transverse shear constraint and one drill rotation constraint on the rotation fields
rotation field between each pair of nodes within each nodal plane. One circumferential transverse shear constraint and one drill rotation constraint on the rotation fields ![]() and
and ![]() are enforced between each pair of nodes on a circumferential line of nodes. In each instance the rotation field is constrained to follow the nodal displacements. To summarize, for element SAXAMN:
are enforced between each pair of nodes on a circumferential line of nodes. In each instance the rotation field is constrained to follow the nodal displacements. To summarize, for element SAXAMN: ![]()
![]()
![]()
![]() has rotated relative to the normal to the shell surface. We define the transverse shear strain as
has rotated relative to the normal to the shell surface. We define the transverse shear strain as ![]()
![]() :
: ![]()
![]()
![]()
![]()
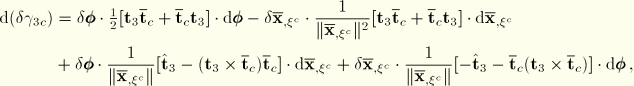
![]()
![]()
![]()
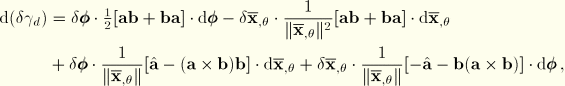

![]() 0° and
0° and ![]() 180°. The edge constraints are broken into two parts: First, a circumferential transverse shear strain is defined that requires that the rotation in the radial direction follow the circumferential rotations at the first and last nodal plane:
180°. The edge constraints are broken into two parts: First, a circumferential transverse shear strain is defined that requires that the rotation in the radial direction follow the circumferential rotations at the first and last nodal plane: ![]()
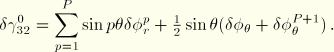
![]()
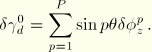

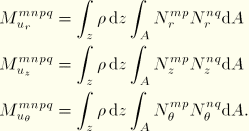
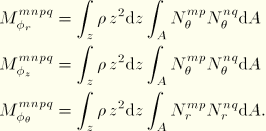
![]()
![]()
![]()
![]()
![]()
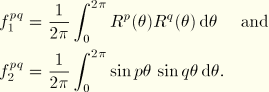
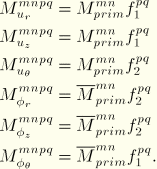
![]() in the Fourier series. After some calculations the following results are obtained:
in the Fourier series. After some calculations the following results are obtained: ![]() :
: ![]()
![]() :
: 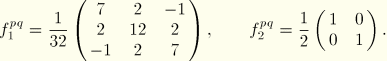
![]() :
: 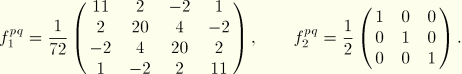
![]() :
: