For structures subjected to continuous harmonic excitation, ABAQUS/Standard offers a “direct” steady-state dynamic analysis procedure in addition to the “modal” procedure described in “Steady-state linear dynamic analysis,” Section 2.5.7, and the “subspace” procedure described in “Subspace-based steady-state dynamic analysis,” Section 2.6.2. This procedure belongs to the perturbation procedures, where the perturbed solution is obtained by linearization about the current base state. For the calculation of the base state, the structure may exhibit material and geometrical nonlinear behavior as well as contact nonlinearities. Viscous damping can be included in the procedure, using the Rayleigh damping coefficients specified under the material definition. Discrete damping (such as dashpot elements) can be included. The procedure can also be used for coupled acoustic-structural medium analysis, including radiation boundary conditions and infinite elements (as described in “Coupled acoustic-structural medium analysis,” Section 2.9.1); with piezoelectric medium (as described in “Piezoelectric analysis,” Section 2.10.1); and with viscoelastic material modeling (as described in “Frequency domain viscoelasticity,” Section 4.8.3). All properties can be frequency dependent.

The formulation is based on the dynamic virtual work equation,

where and are the velocity and the acceleration, is the density of the material, is the mass proportional damping factor (part of the Rayleigh damping assumption), is the stress, is the surface traction, and is the strain variation that is compatible with the displacement variation . The discretized form of this equation iswhere the following definitions apply:

For the steady-state harmonic response we assume that the structure undergoes small harmonic vibrations about a deformed, stressed state, defined by the subscript 0. Since steady-state dynamics belongs to the perturbation procedures, the load and response in the step define the change from the base state. The change in internal force vector follows by linearization:

The change in stress can be written in the formwhere is the elasticity matrix for the material and is the stiffness proportional damping factor (the other part of the Rayleigh damping assumption). The strain and strain rate changes follow from the displacement and velocity changes: This allows us to write Equation 2.6.1–2 as where we have defined the stiffness matrix and the stiffness damping matrix

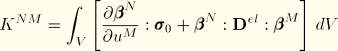
For harmonic excitation and response we can write

where and are the real and imaginary parts of the amplitudes of the displacement, and are the real and imaginary parts of the amplitude of the force applied to the structure and is the circular frequency. Substituting the expressions for harmonic excitation and response in Equation 2.6.1–4 and writing the result in matrix form yieldswhere Note that both the real and imaginary parts of are symmetric.

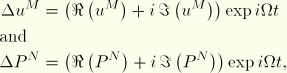
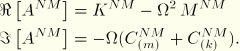
The procedure is activated by defining a direct-solution steady-state dynamic analysis step. Both real and imaginary loads can be defined.

As output ABAQUS/Standard provides amplitudes and phases for all element and nodal variables at the requested frequencies. For this procedure all amplitude references must be given in the frequency domain.