The piezoelectric effect is governed by coupled mechanical equilibrium and electric flux conservation equations.

The mechanical equilibrium equation is

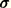
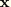
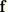
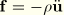
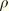
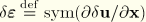
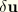
where is the “true” (Cauchy) stress at a point currently at ; is the traction across a point of the surface of the body; is the body force per unit volume in the body (such as the d'Alembert force , in which is the density of the body); and , where is an arbitrary, continuous vector field (the virtual velocity field).

The electrical flux conservation equation is

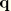
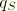
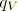
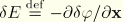
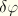
where is the electric flux vector; is the electric flux per unit area entering the body at a point on its surface; is the electric flux entering the body per unit volume; and , where is an arbitrary, continuous, scalar field (the virtual potential). These quantities are also known by other terms that are frequently used within electrical engineering references. The electric flux vector q is known as the electrical displacement, and the potential gradient E is known as the electrical field.

Currently the assumption of linear materials is utilized. The basic equations for a piezoelectric linear medium are defined in the following. Following Ikeda (1990), three alternative forms of the constitutive equations are presented:

e-form:

d-form:

g-form:

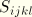
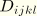
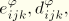
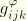
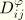
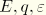
where are the material compliances; are the material stiffnesses; and are piezoelectric constants; and are the dielectric constants. In these equations the superscript , or above a particular property indicates that the property is defined at zero electrical gradient, at zero electrical displacement, at zero strain, and at zero stress, respectively. Since all these forms describe the same constitutive relationships, the different mechanical and piezoelectrical constants can be expressed in terms of one another. The following relationships exist among the properties (Ikeda, 1990):In ABAQUS the constitutive equations in the e-form are used:These are expressed in terms of the piezoelectric stress coefficient matrix . 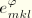However, ABAQUS also allows the input of piezoelectric constants in terms of the piezoelectric strain coefficient matrix .

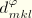
The constitutive equations in the g-form can also be expressed as

and These equations can be convenient in interpreting and verifying the results of piezoelectrical analyses.

For the piezoelectric elements both displacements and electric potentials exist at the nodal locations. The displacements and electrical potentials are approximated within the element as

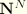
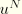
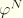
and where is the array of interpolating functions and and are nodal quantities. The body forces and charges as well as the surface forces and charges are interpolated in a similar manner.

The strains and electrical potential gradients are given as

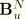
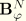
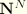
and where and are the spatial derivatives of . In geometrically nonlinear analyses these spatial derivatives are defined in the current configuration.

With these approximate fields and the constitutive properties given above, in conjunction with the equilibrium and conservation equations, the following system of equations is derived in terms of nodal quantities:

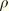
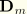
and where is the mass matrix (no inertia terms exist for the electrical flux conservation equation), is the mass density, is the displacement stiffness matrix, is the dielectric “stiffness” matrix, is the piezoelectric coupling matrix, is the mechanical force vector, and is the electrical charge vector. 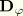In these expressions the constitutive properties are specified in a matrix form where is the mechanical relationship, is the electrical relationship, and is the piezoelectrical relationship. The “load” vectors include the body, surface, and concentrated quantities, as shown. The unknowns are the nodal displacements and potentials. Once these are determined, the strains and potential gradients can be computed using the expressions given above. The stresses and electrical flux densities are computed by means of constitutive relationships.