2.5.7 Steady-state linear dynamic analysis

Steady-state linear dynamic analysis predicts the linear response of a structure subjected to continuous harmonic excitation. In many cases steady-state linear dynamic analysis in ABAQUS/Standard uses the set of eigenmodes extracted in a previous eigenfrequency step to calculate the steady-state solution as a function of the frequency of the applied excitation. ABAQUS/Standard also has a “direct” steady-state linear dynamic analysis procedure, in which the equations of steady harmonic motion of the system are solved directly without using the eigenmodes, and a “subspace” steady-state linear dynamic analysis procedure, in which the equations are projected onto a subspace of selected eigenmodes of the undamped system. These options are intended for systems in which the behavior is dependent on frequency, for when the model includes damping, or for systems in which the governing equations are not symmetric.
This section describes the linear steady-state response procedure based on the eigenmodes.
The projection of the equations of motion of the system onto the 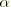 th mode gives
th mode gives
where

is the amplitude of mode
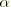
(the
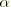
th “generalized coordinate”),
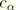
is the damping associated with this mode (see below),
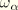
is the undamped frequency of the mode,
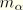
is the generalized mass associated with the mode, and
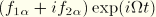
is the forcing associated with this mode. The forcing is defined by the frequency,
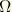
, and the real and imaginary parts of the nodal equivalent forces,
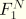
and
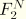
, projected onto the eigenmode
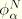
:
In this equation summation is implied by the repeat of the superscript
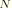
indicating a degree of freedom in the model; but throughout this section we are working with only a single modal equation, so no summation is implied by the repeat of the mode subscript

. The load vector is written in terms of its real and imaginary parts,
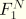
and
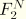
, since this is the manner in which the loading is defined in ABAQUS/Standard (as load case 1 and load case 2). It is equivalently possible to write the loading in terms of its magnitude,
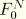
, and phase,
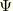
, as
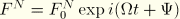
, where
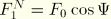
and
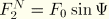
.
Several representations of modal damping are provided. Modal damping defines 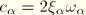 , where
, where 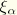 is the fraction of critical damping in the mode. Structural damping gives a damping force proportional to the modal amplitude:
is the fraction of critical damping in the mode. Structural damping gives a damping force proportional to the modal amplitude:
where
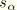
is the structural damping coefficient for the mode. Rayleigh damping is defined by
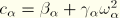
;
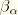
and
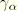
are the Rayleigh coefficients damping low and high frequency modes, respectively. Rayleigh damping can be reproduced exactly by modal damping as
Introducing all of these damping definitions into
Equation 2.5.7–1 gives
The solution to this equation is
where
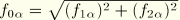
is the amplitude of the projected load vector and
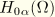
is the amplitude of the complex “transfer function” for mode
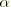
.
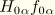
defines the response in mode
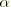
from the force projection onto that mode and is defined by its real and imaginary parts as
where
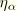
denotes
The amplitude of the response is
and the phase angle of the response is
If a harmonic base motion is applied, the real and imaginary parts of the modal loads are given as
where
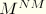
is the structure's mass matrix and
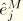
is a vector that has unit magnitude in the direction of the base acceleration at any grounded node and is otherwise zero;
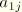
and
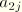
are the real and imaginary parts of the base acceleration. If the base motion is given as a velocity or displacement, the corresponding accelerations are
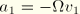
and
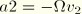
, where
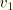
and
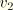
are the real and imaginary parts of the velocity, or
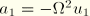
and
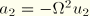
, where
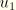
and
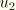
are the real and imaginary parts of the displacement.
The peak amplitude of any physical variable, 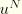 , is available from the modal amplitudes as
, is available from the modal amplitudes as
Steady-state response is given as a frequency sweep through a user-specified range of frequencies. Since the structural response peaks around the natural frequencies, a bias function is used to cluster the response points around the frequencies. The biasing is described in “Mode-based steady-state dynamic analysis,” Section 6.3.8 of the ABAQUS Analysis User's Manual.

![]() th mode gives
th mode gives ![]()
![]() , where
, where ![]() is the fraction of critical damping in the mode. Structural damping gives a damping force proportional to the modal amplitude:
is the fraction of critical damping in the mode. Structural damping gives a damping force proportional to the modal amplitude: ![]()
![]()
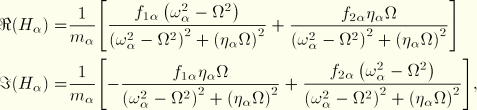
![]()
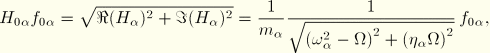
![]()
![]()
![]()
![]() , is available from the modal amplitudes as
, is available from the modal amplitudes as ![]()