1.5.5 Energy balance

Products: ABAQUS/Standard ABAQUS/Explicit
The conservation of energy implied by the first law of thermodynamics states that the time rate of change of kinetic energy and internal energy for a fixed body of material is equal to the sum of the rate of work done by the surface and body forces. This can be expressed as
where
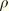
is the current mass density,
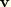
is the velocity field vector,
U
is the internal energy per unit mass,

is the surface traction vector,
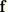
is the body force vector, and
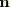
is the normal direction vector on boundary S.
Using Gauss' theorem and the identity that 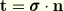 on the boundary S, the first term of the right-hand side of Equation 1.5.5–1 can be rewritten as
on the boundary S, the first term of the right-hand side of Equation 1.5.5–1 can be rewritten as
where we have used the fact that
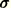
is symmetric, and we also know (see
“Equilibrium and virtual work,” Section 1.5.1) that
where
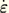
is the strain rate tensor (see
“Rate of deformation and strain increment,” Section 1.4.3). Substituting
Equation 1.5.5–2 into
Equation 1.5.5–1 yields
From Cauchy's equation of motion we have
Substituting this into
Equation 1.5.5–3 gives
From this we get the energy equation
Integrating this equation we find
where
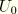
is the energy at time
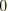
. To make the energy balance (
Equation 1.5.5–1) more convenient to use, we integrate it in time:
or
where
defined as the rate of work done to the body by external forces and contact friction forces between the contact surfaces.

, the kinetic energy, is given by
and
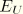
is defined as
To track physically distinguishable engineering phenomena more narrowly, we introduce decompositions of the stress, strain, and tractions.
We can split the traction,  , into the surface distributed load,
, into the surface distributed load, 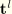 , the solid infinite element radiation traction,
, the solid infinite element radiation traction, 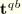 , and the frictional traction,
, and the frictional traction, 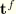 . Then
. Then 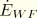 can be written as
can be written as
where
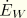
is the rate of work done to the body by external forces,
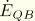
is the rate of energy dissipated by the damping effect of solid medium infinite elements, and
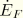
is the rate of energy dissipated by contact friction forces between the contact surfaces. An energy balance for the entire model can then be written as
For convenience, the dissipated portions of the internal energy are split off:
where
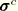
is the stress derived from the user-specified constitutive equation, without viscous dissipation effects included;
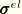
is the elastic stress;
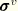
is the viscous stress (defined for bulk viscosity, material damping, and dashpots);
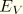
is the energy dissipated by viscous effects; and
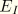
is the remaining energy, which we continue to call the internal energy. If we introduce the strain decomposition,
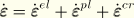
(where
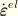
,
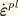
, and
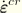
are elastic, plastic, and creep strain rates, respectively), the internal energy,
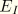
, can be expressed as
where
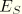
is the applied elastic strain energy,
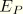
is the energy dissipated by plasticity, and
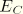
is the energy dissipated by time-dependent deformation (creep, swelling, and viscoelasticity).
If damage occurs in the material, not all of the applied elastic strain energy is recoverable. At any given time, the stress, 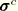 , can be expressed in terms of the “undamaged” stress,
, can be expressed in terms of the “undamaged” stress, 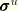 , and the continuum damage parameter, d:
, and the continuum damage parameter, d:
The damage parameter,
d, starts at zero (undamaged material) and increases to a maximum value of no more than one (fully damaged material). Hence, we can write
We assume that, upon unloading, the damage parameter remains fixed at the value attained at time
t. Therefore, the recoverable strain energy is equal to
and the energy dissipated through damage is equal to
If we define
as the undamaged elastic energy function, we can write
and
Interchanging the integrals yields
and
The first term in the last expression vanishes, since at time
t,
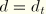
and at time zero,
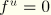
. If we now define the damage strain energy function
then
For a linear elastic energy function
and, hence,

![]()
![]()
![]()
![]()
![]()
![]() on the boundary S, the first term of the right-hand side of Equation 1.5.5–1 can be rewritten as
on the boundary S, the first term of the right-hand side of Equation 1.5.5–1 can be rewritten as![]()
![]()
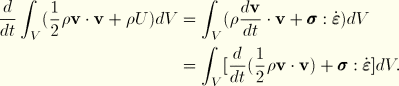
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]() , into the surface distributed load,
, into the surface distributed load, ![]() , the solid infinite element radiation traction,
, the solid infinite element radiation traction, ![]() , and the frictional traction,
, and the frictional traction, ![]() . Then
. Then ![]() can be written as
can be written as ![]()
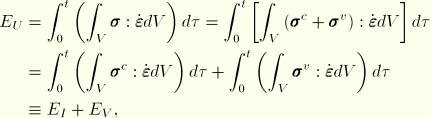
![]() , can be expressed in terms of the “undamaged” stress,
, can be expressed in terms of the “undamaged” stress, ![]() , and the continuum damage parameter, d:
, and the continuum damage parameter, d:![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
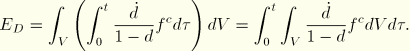
![]()
![]()