
Products: ABAQUS/Standard ABAQUS/Explicit
Many of the materials we need to model are path dependent, so usually the constitutive relationships are defined in rate form, which requires a definition of strain rate. The velocity of a material particle is
![]()
The velocity difference between two neighboring particles in the current configuration is
![]()
In “Deformation,” Section 1.4.1, we introduced the definition of the deformation gradient matrix, ![]() :
:
![]()
![]()
We could also obtain the velocity difference directly by
![]()
![]()
Comparing the two expressions for ![]() in terms of the reference configuration gauge length
in terms of the reference configuration gauge length ![]() , we see that
, we see that
![]()
![]()
Now ![]() will be composed of a rate of deformation and a rate of rotation or spin. Since these are rate quantities, the spin can be treated as a vector; thus, we can decompose
will be composed of a rate of deformation and a rate of rotation or spin. Since these are rate quantities, the spin can be treated as a vector; thus, we can decompose ![]() into a symmetric strain rate matrix and an antisymmetric rotation rate matrix, just as in small motion theory we decompose the infinitesimal displacement gradient into an infinitesimal strain and an infinitesimal rotation. The symmetric part of the decomposition is the strain rate (it is called the rate of deformation tensor in many textbooks and is also commonly denoted as
into a symmetric strain rate matrix and an antisymmetric rotation rate matrix, just as in small motion theory we decompose the infinitesimal displacement gradient into an infinitesimal strain and an infinitesimal rotation. The symmetric part of the decomposition is the strain rate (it is called the rate of deformation tensor in many textbooks and is also commonly denoted as ![]() ) and is
) and is
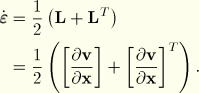
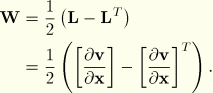
These are particularly simple and familiar forms; for example, ![]() is identical to the elementary definition of “small strain” if we replace the particle velocity,
is identical to the elementary definition of “small strain” if we replace the particle velocity, ![]() , with the displacement,
, with the displacement, ![]() . In one dimension
. In one dimension ![]() is
is
![]()
![]()
This interpretation would also be correct if the principal directions of strain rotate along with the rigid body motion (because the identification can be applied to each principal value of the logarithmic strain matrix). In the general case, when the principal strain directions rotate independent of the material, ![]() is not integrable into a total strain measure. Nevertheless, the identification of
is not integrable into a total strain measure. Nevertheless, the identification of ![]() with the rate of logarithmic strain in the particular case of nonrotating principal directions provides a useful interpretation of the logarithmic measure of strain as a “natural” strain if we think of
with the rate of logarithmic strain in the particular case of nonrotating principal directions provides a useful interpretation of the logarithmic measure of strain as a “natural” strain if we think of ![]() , as it is defined above as the symmetric part of the velocity gradient with respect to current spatial position, as a “natural” measure of strain rate.
, as it is defined above as the symmetric part of the velocity gradient with respect to current spatial position, as a “natural” measure of strain rate.
The typical inelastic constitutive model requires as input a small but finite strain increment ![]() , as well as vector and tensor valued state variables (such as the stress) that are written on the current configuration. In ABAQUS/Explicit and for shell and membrane elements in ABAQUS/Standard, a slightly different algorithm is used to calculate
, as well as vector and tensor valued state variables (such as the stress) that are written on the current configuration. In ABAQUS/Explicit and for shell and membrane elements in ABAQUS/Standard, a slightly different algorithm is used to calculate ![]() . For most element types in ABAQUS/Standard we approach this problem by first using the polar decomposition in the increment to define the change in the average material rotation over the increment,
. For most element types in ABAQUS/Standard we approach this problem by first using the polar decomposition in the increment to define the change in the average material rotation over the increment, ![]() , from the total deformation in the increment,
, from the total deformation in the increment, ![]() :
:
![]()
![]()
![]()
These rotated variables are now passed to the constitutive routines, which may provide further updates to them because of constitutive effects. These constitutive effects will be associated with deformation, which must be supplied in the form of the strain increment ![]() . For this we proceed as follows.
. For this we proceed as follows.
Since we assume ![]() rotates the deformation basis—in the sense that it rotates the principal axes of deformation and, thus, provides a measure of average material rotation—we can define the velocity gradient
rotates the deformation basis—in the sense that it rotates the principal axes of deformation and, thus, provides a measure of average material rotation—we can define the velocity gradient ![]() at any time during the increment, referred to the fixed basis at
at any time during the increment, referred to the fixed basis at ![]() , as
, as
![]()
![]()
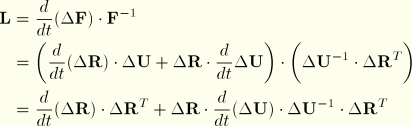
![]()
We now assume that the incremental stretch at any time in the increment written on the basis at the beginning of the increment, ![]() , always has the same principal directions
, always has the same principal directions ![]() ,
, ![]() ,
, ![]() , so that
, so that
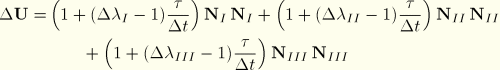
![]()
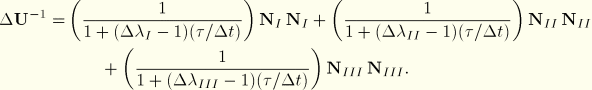
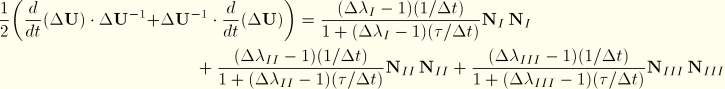
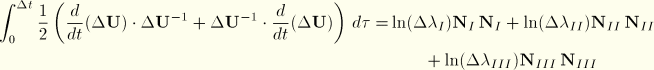
![]()