Many of the constitutive models in ABAQUS require tensors to be stored to define the state at a material calculation point. Such “material state tensors” are stored as their components in a local, orthonormal, system at the material calculation point. The orientation of that system with respect to the global spatial system is stored as a rotation from the global axis system. The purpose of this section is to define the manner in which such tensors are stored and updated.

Three types of local basis are used in ABAQUS for material calculations. For isotropic materials in continuum elements the global, spatial, system is used—the material basis is fixed in time. For isotropic materials in structural surface elements (shells and membranes) the local system is defined by the standard ABAQUS convention described in “Conventions,” Section 1.2.2 of the ABAQUS Analysis User's Manual; and for beams and trusses it is defined with the 1-direction along the axis of the member and the 2- and 3-directions in material directions in the cross-section. Thus, with isotropic materials the material basis is always the same as the element basis, although for structural elements the material basis changes with time. For anisotropic materials the material basis must be defined by the user and rotates with the average rigid body spin of the material. In this case the material basis and the element basis are not the same.

We refer to this local material basis at time t as , where the superscript indicates that the basis is associated with material calculations and means that the basis is taken at time t. In this section Latin subscripts (like the above) take the range 1–3, while Greek subscripts will take the range 1–2.

Any tensor associated with the material's state, , say (such as the stress tensor ), is stored in terms of its components along the material basis:

The increment from time t to time of local motion at the material calculation point is defined by the incremental deformation gradient,

This matrix is calculated from the gradient interpolator of the finite element and the coordinates of the element's nodes at times t and .

The polar decomposition of is

where is the average rigid body rotation at the material point and is a pure stretch matrix: (here is a principal stretch ratio and is a principal stretch direction).

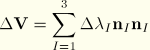
During an increment any material state tensor changes according to

where is the change in caused by constitutive behavior and is the average incremental rigid body rotation of the material. Since material tensors are written in terms of their components in the material basis system, this update is computed as It is, therefore, necessary to project onto the material basis systems at the start and end of the increment to define the update of material tensor components:

For isotropic materials the have been chosen for geometric convenience only, so the are quite general.

For anisotropic materials the material basis system, , rotates with the average rigid body rotation of the material, , and so is updated by

In this case we see that and so the update of a material tensor's components simplifies to However, since in this case the material basis system is not the same as the element basis system, (which is chosen for geometric convenience for element calculations), transformations must be done to change basis system. Specifically, at the start of the material calculation routines, the strain increments are rotated from the element basis into the material basis: Likewise, at the end of the material calculation routines, the stress increments are rotated back to the element basis for integration into the discretized approximation to the equilibrium equations: In addition, the material stiffness matrix, must also be rotated from the material basis to the element basis: For a shell or membrane only two-dimensional rotations are required—for example, since because both are unit vectors along the normal to the surface.