“Loading rates,” Section 13.2, discusses the procedures for determining the appropriate step time for a quasi-static process. We can determine an approximate lower bound on step time duration if we know the lowest natural frequency, the fundamental frequency, of the blank. One way to obtain such information is to run a frequency analysis in ABAQUS/Standard. In this forming analysis the punch deforms the blank into a shape similar to the lowest mode. Therefore, it is important that the time for the first forming stage is greater than or equal to the time period for the lowest mode if you wish to model structural, as opposed to localized, deformation.

The goal of the forming process is to quasi-statically form a channel with a punch displacement of 0.03 m. In selecting loading rates for quasi-static analyses, it is recommended that you begin with faster loading rates and decrease the loading rates as necessary to converge on a quasi-static solution more quickly. However, if you wish to increase the likelihood of a quasi-static result in your first analysis attempt, you should consider step times that are a factor of 10 to 50 times slower than that corresponding to the fundamental frequency. In this analysis you will start with a time period of 0.007 s for the forming analysis step. This is based on the frequency analysis performed in ABAQUS/Standard, which shows that the blank has a fundamental frequency of 140 Hz, corresponding to a time period of 0.00714 s. This time period corresponds to a constant punch velocity of 4.3 m/s. You will examine the kinetic and internal energy results carefully to check that the solution does not include significant dynamic effects.

Copy the Standard model to a model named Explicit. Make all subsequent model changes to the Explicit model. To begin, edit the Steel material definition to include a mass density of 7800 kg/m³.

In the ABAQUS/Standard analysis an initial gap is modeled between the punch and the blank to aid the contact calculations. It is not necessary to take this precaution in the ABAQUS/Explicit analysis. Therefore, in the Assembly module, translate the punch –0.001 m in the U2 direction. Click Yes in the warning dialog box that appears regarding relative and absolute constraints.

A concentrated force is applied to the blank holder. To compute the dynamic response of the holder, a point mass must be assigned to its rigid body reference point. The actual mass of the holder is not important; what is important is that the mass should be of the same order of magnitude as the mass of the blank (0.78 kg) to minimize noise in the contact calculations. Choose a point mass value of 0.1 kg. To assign the mass, expand Engineering Features underneath the Assembly container in the Model Tree. In the list that appears, double-click Inertias. In the Create Inertia dialog box that appears, enter the name PointMass and click Continue. Select the set RefHolder, and assign it a mass of 0.1 kg.

You need to create two steps for the ABAQUS/Explicit analysis. In the first step the holder force is applied; in the second step the punch stroke is applied. Delete all steps except the step named Establish Contact I. Replace this step with a single explicit dynamics step. Enter the step description Apply holder force, and specify a time period of 0.0001 s. This time period is appropriate for the application of the holder force because it is long enough to avoid dynamic effects but short enough to prevent a significant impact on the run time for the job. Rename this step Holder force. Create a second explicit dynamics step named Displace punch with a time period of 0.007 s. Enter Apply punch stroke as the step description.

To help determine how closely the analysis approximates the quasi-static assumption, the various energy histories will be useful. Especially useful is comparing the kinetic energy to the internal strain energy. The energy history is written to the output database file by default.

For the first attempt of this metal forming analysis, you will use tabular amplitude curves with the default smoothing parameter for both the application of the holder force and the punch stroke. Create a tabular amplitude curve for application of the holder force named Ramp1. Enter the amplitude data in Table 13–1. Define a second tabular amplitude curve for the punch stroke named Ramp2. Enter the amplitude data in Table 13–2.

Open the Load Manager, and create a concentrated force named RefHolderForce in the step named Holder force. Specify RefHolder for the point of application and a magnitude of -440000 in the CF2 direction. Change the amplitude definition for this load to Ramp1.

Open the Boundary Condition Manager, and delete the boundary conditions named MidLeftBC and MidRightBC. Edit the RefDieBC boundary condition so that the constraint in the U2 direction is zero in the Holder force step. Do not change the constraints in the other directions. Remove the constraint in the U2 direction for the RefHolderBC boundary condition, and leave the constraints in the other directions unchanged. Change the displacement boundary condition RefPunchBC in the U2 direction to –0.03 m in the Displace Punch step. Use the amplitude curve Ramp2 for this boundary condition.

In this model you will monitor the vertical displacement (degree of freedom 2) of the punch's reference node throughout the step. Because the DOF Monitor was set to monitor the vertical displacement of RefPunch in the ABAQUS/Standard forming analysis, you do not need to make any changes.

Change the family of the elements used to mesh the blank to Explicit, and specify enhanced hourglass control. Mesh the blank. The tools have been modeled with analytical surfaces so they do not need to be meshed.

Create a job named Forming-1. Give the job the following description: Channel forming -- attempt 1.

Before you run the forming analysis, you may wish to know how many increments the analysis will take and, consequently, how much computer time the analysis requires. You can run a data check analysis to obtain the approximate value for the initial stable time increment, or you can estimate it using the relations in “Mass scaling,” Section 13.3. Knowing the stable time increment, which in this case does not change much from increment to increment, you can determine how many increments are required to complete the forming stage. Once the analysis begins, you can get an idea of how much CPU time is required per increment and, consequently, how much CPU time the analysis requires.

Using the relations stated in “Mass scaling,” Section 13.3, the stable time increment for this analysis is approximately 1 × 10^–7 s. Therefore, the forming stage requires approximately 185,000 increments for a step time of 0.007 s.

Save your model to a model database file, and submit the job for analysis. Monitor the solution progress; correct any modeling errors that are detected, and investigate the cause of any warning messages. Ten minutes or more may be required to run this analysis to completion.

Once the analysis is underway, an X–Y plot of the values of the degree of freedom that you selected to monitor (the punch's vertical displacement) appears in a separate viewport. From the main menu bar, select ViewportJob Monitor: Forming-1 to follow the progression of the punch's displacement in the 2-direction over time as the analysis runs.

Before looking at the results that are ultimately of interest, such as stresses and deformed shapes, we need to determine whether or not the solution is quasi-static. One good approach is to compare the kinetic energy history to the internal energy history. In a metal forming analysis most of the internal energy is due to plastic deformation. In this model the blank is the primary source of kinetic energy (the motion of the holder is negligible, and the punch and die have no mass associated with them). To determine whether an acceptable quasi-static solution has been obtained, the kinetic energy of the blank should be no greater than a few percent of its internal energy. For greater accuracy, especially when springback stresses are of interest, the kinetic energy should be lower. This approach is very useful because it applies to all types of metal forming processes and does not require any intuitive understanding of the stresses in the model; many forming processes may be too complex to permit an intuitive feel for the results.

While a good primary indication of the caliber of a quasi-static analysis, the ratio of kinetic energy to internal energy alone is not adequate to confirm the quality. You should also evaluate the two energies independently to determine whether they are reasonable. This part of the evaluation takes on increased importance when accurate springback stress results are needed because an accurate springback stress solution is highly dependent on accurate plasticity results. Even if the kinetic energy is fairly small, if it contains large oscillations, the model could be experiencing significant plasticity. Generally, we expect smooth loading to produce smooth results; if the loading is smooth but the energy results are oscillatory, the results may be inadequate. Since an energy ratio is incapable of showing such behavior, you should also study the kinetic energy history itself to see whether it is smooth or noisy.

If the kinetic energy does not indicate quasi-static behavior, it can be useful to look at velocity histories at some nodes to get an understanding of the model's behavior in various regions. Such velocity histories can indicate which regions of the model are oscillating and causing the high kinetic energies.

Enter the Visualization module, and open the output database created by this job (Forming-1.odb). Plot the whole model kinetic (ALLKE) and internal (ALLIE) energies.

History plots of the kinetic and internal energies for the whole model appear as shown in Figure 13–9 and Figure 13–10, respectively.

The kinetic energy history shown in Figure 13–9 oscillates significantly. In addition, the kinetic energy history has no clear relation to the forming of the blank, which indicates the inadequacy of this analysis. In this analysis the punch velocity remains constant, while the kinetic energy—which is primarily due to the motion of the blank—is far from constant.

Comparing Figure 13–9 and Figure 13–10 shows that the kinetic energy is a small fraction (less than 1%) of the internal energy through all but the very beginning of the analysis. The criterion that kinetic energy must be small relative to internal energy has been satisfied, even for this severe loading case.

Although the kinetic energy of the model is a small fraction of the internal energy, it is still quite noisy. Therefore, we should change the simulation in some way to obtain a smoother response.

The kinetic energy history is shown in Figure 13–11. The response of the kinetic energy is clearly related to the forming of the blank: the value of kinetic energy peaks in the middle of the second step, corresponding to the time when the punch velocity is the greatest. Thus, the kinetic energy is appropriate and reasonable.

The internal energy for attempt 2, shown in Figure 13–12, shows a smooth increase from zero up to the final value. Again, the ratio of kinetic energy to internal energy is quite small and appears to be acceptable.

Now that we are satisfied that the quasi-static solution for the forming analysis is adequate, we can study some of the other results of interest. Figure 13–14 shows a comparison of the Mises stress in the blank obtained with ABAQUS/Standard and ABAQUS/Explicit.

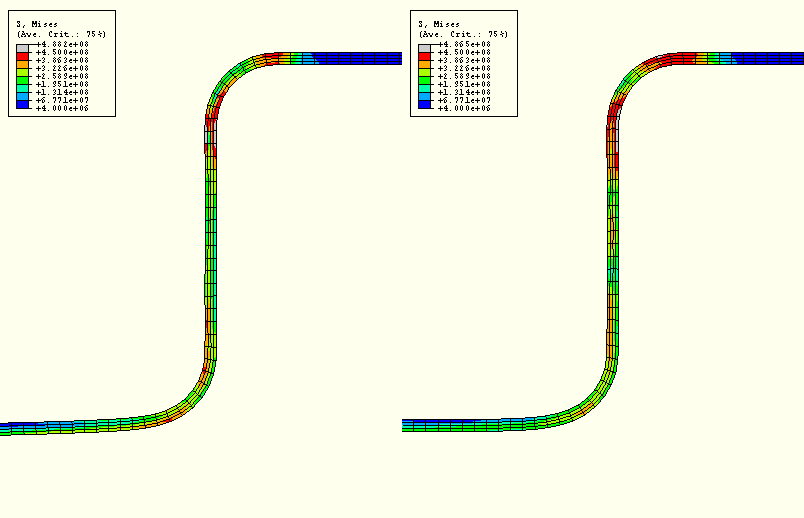
The plot shows that the peak stresses in the ABAQUS/Standard and ABAQUS/Explicit analyses are within 1% of each other and that the overall stress contours of the blank are very similar. To further examine the validity of the quasi-static analysis results, you should compare the equivalent plastic strain results and final deformed shapes from the two analyses.

Figure 13–15 shows contour plots of the equivalent plastic strain in the blank, and Figure 13–16 shows an overlay plot of the final deformed shape predicted by the two analyses.

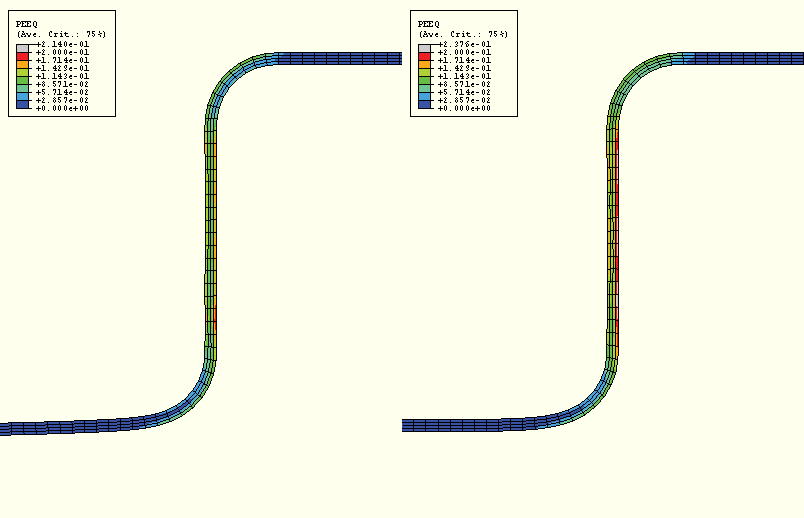
You should also compare the steady punch force predicted by the ABAQUS/Standard and ABAQUS/Explicit analyses. As seen in Figure 13–17, the steady punch force predicted by ABAQUS/Explicit is approximately 12% higher than that predicted by ABAQUS/Standard. The differences between the ABAQUS/Standard and ABAQUS/Explicit results are primarily due to two factors. First, ABAQUS/Explicit regularizes the material data. Second, friction effects are handled slightly differently in the two analysis products; ABAQUS/Standard uses penalty friction, whereas ABAQUS/Explicit uses kinematic friction.

“Loading rates,” Section 13.2, and “Metal forming problems,” Section 13.2.3, discuss how to determine acceptable scaling of the loading rate or mass to accelerate the time scale of a quasi-static analysis. The goal is to model the process in the shortest time period in which inertial forces remain insignificant. There are bounds on how much the solution time can be increased while still obtaining a meaningful quasi-static solution.

As discussed in “Loading rates,” Section 13.2, we can use the same methods to determine an appropriate mass scaling factor as we would use to determine an appropriate load rate scaling factor. The difference between the two methods is that a load rate scaling factor of has the same effect as a mass scaling factor of . Originally, we assumed that a step time on the order of the period of the fundamental frequency of the blank would be adequate to produce quasi-static results. By studying the model energies and other results, we were satisfied that these results were acceptable. This technique produced a punch velocity of approximately 4.3 m/s. Now we will accelerate the solution time using mass scaling and compare the results against our unscaled solution to determine whether the scaled results are acceptable. We assume that scaling can only diminish, not improve, the quality of the results. The objective is to use scaling to decrease the computer time and still produce acceptable results.

Our goal is to determine what scaling values still produce acceptable results and at what point the scaled results become unacceptable. To see the effects of both acceptable and unacceptable scaling factors, we investigate a range of scaling factors on the stable time increment size from to 5; specifically, we choose , , and 5. These speedup factors translate into mass scaling factors of 5, 10, and 25, respectively.

Save your model, and submit the job for analysis. Monitor the solution progress; correct any modeling errors that are detected, and investigate the cause of any warning messages.

When the job is finished, change the mass scaling factor to 10. Create and run a new job named Forming-4--sqrt10. When this job has completed, change the mass scaling factor again to 25; create and run a new job named Forming-5--5. For each of the last two jobs, modify the job descriptions as appropriate.

First, we will look at the effect of mass scaling on the equivalent plastic strains and the displaced shape. We will then see whether the energy histories provide a general indication of the analysis quality.

One of the results of interest in this analysis is the equivalent plastic strain, PEEQ. Since we have already seen the contour plot of PEEQ at the completion of the unscaled analysis in Figure 13–15, we can compare the results from each of the scaled analyses with the unscaled analysis results. Figure 13–18 shows PEEQ for a speedup of (mass scaling of 5), Figure 13–19 shows PEEQ for a speedup of (mass scaling of 10), and Figure 13–20 shows PEEQ for a speedup of 5 (mass scaling of 25). Figure 13–21 compares the internal and kinetic energy histories for each case of mass scaling. The mass scaling case using a factor of 5 yields results that are not significantly affected by the increased loading rate. The case with a mass scaling factor of 10 shows a high kinetic-to-internal energy ratio, yet the results seem reasonable when compared to those obtained with slower loading rates. Thus, this is likely close to the limit on how much this analysis can be sped up. The final case, with a mass scaling factor of 25, shows evidence of strong dynamic effects: the kinetic-to-internal energy ratio is quite high, and a comparison of the final deformed shapes among the three cases demonstrates that the deformed shape is significantly affected in the last case.

As the mass scaling increases, the solution time decreases. The quality of the results also decreases because dynamic effects become more prominent, but there is usually some level of scaling that improves the solution time without sacrificing the quality of the results. Clearly, a speedup of 5 is too great to produce quasi-static results for this analysis.

A smaller speedup, such as , does not alter the results significantly. These results would be adequate for most applications, including springback analyses. With a scaling factor of 10 the quality of the results begins to diminish, while the general magnitudes and trends of the results remain intact. Correspondingly, the ratio of kinetic energy to internal energy increases noticeably. The results for this case would be adequate for many applications but not for accurate springback analysis.

Figure 13–22 overlays (ViewOverlay Plot) the deformed shape of the blank after the forming and springback stages (the forming stage corresponds to frame 0 in the output database file, while the springback stage corresponds to the final frame). The springback result is necessarily dependent on the accuracy of the forming stage preceding it. In fact, springback results are highly sensitive to errors in the forming stage, more sensitive than the results of the forming stage itself.

You should also plot the blank's internal energy ALLIE and compare it with the static stabilization energy ALLSD that is dissipated. The stabilization energy should be a small fraction of the internal energy to have confidence in the results. Figure 13–23 shows a plot of these two energies; the static stabilization energy is indeed small and, thus, has not significantly affected the results.