25.2.15 RSURFU

25.2.15 `RSURFU`
User subroutine to define a rigid surface.

Product: ABAQUS/Standard

References

Overview

User subroutine RSURFU:

is used to define the surface of a rigid body for use with user-subroutine-defined contact surfaces;
can be used to define a complex rigid surface if the various capabilities provided for defining a surface in ABAQUS (see “Defining analytical rigid surfaces,” Section 2.3.4) are too restrictive;
will be called at each slave node of a contact pair or, if contact elements are used, at each integration point of each contact element with which the rigid surface is associated; and
requires the definition of the closest point on the rigid surface, the normal and tangent directions, and the surface curvature.

Overpenetration constraint

This routine must determine if a slave node has penetrated the rigid surface and define the local surface geometry. If the deforming and rigid surfaces are in contact at this point, ABAQUS/Standard will impose a constraint at the point to prevent overpenetration. The local surface geometry must be defined to provide the necessary orientation for the constraint equations and friction directions and to allow ABAQUS/Standard to compute the rate of change of these equations as the point moves around on the surface—the “tangent stiffness matrix” for the surface in the Newton algorithm. For the purpose of these calculations, it is best to define a smooth surface. If the surface is defined in a discontinuous manner, convergence may be adversely affected.

Calculations to be performed

Each time RSURFU is called, ABAQUS/Standard gives the current position of point on the surface of the deforming structure, ; the current position of the rigid body reference point, ; the total displacements of both of these points, and ; and the total rotation of the rigid body reference point, .

The routine should perform the following calculations:

A point, , must be found on the rigid surface at which the normal to the surface passes through . If there is not a unique point , the routine must choose the most suitable point (usually the closest to ). The routine must pass back the coordinates of to ABAQUS/Standard.
RSURFU must define the distance, , by which has penetrated the surface below . A negative value of means that is outside the surface of the rigid body.
If the surfaces are in contact, which may sometimes be the case even if is negative, RSURFU must define the local surface geometry.

Defining the local surface geometry

There are two scenarios under which it is mandatory that the routine define the local surface geometry: if has penetrated the surface— if the surface behavior is truly rigid, or is greater than the maximum overclosure value specified for modified surface behavior using either contact controls (see “Common difficulties associated with contact modeling in ABAQUS/Standard,” Section 21.2.9) or a modified pressure-overclosure relationship (see “Contact pressure-overclosure relationships,” Section 22.1.2)—and if was in contact at the beginning of the increment, in which case the flag LCLOSE=1 (see the variable list for the definition of LCLOSE). The routine can be coded so that local surface geometry definitions are always provided regardless of the scenario.

The local surface geometry is specified by two orthogonal tangents to the rigid surface at , as well as the rates of change of the outward pointing normal at , , with respect to local surface coordinates that are distance measuring along the tangents, and (see Figure 25.2.15–1). The tangents to the surface at must be defined so that their positive, right-handed cross product is the outward normal to the surface. For two-dimensional cases ABAQUS/Standard assumes that the second tangent is (0, 0, –1), so that when you give the direction cosines of the first tangent as (, , 0), the outward normal will be (, , 0). The rates of change of the normal with respect to and are required to define the local curvature of the surface.

Figure 25.2.15–1 Local geometry on a rigid surface.

User subroutine interface

SUBROUTINE RSURFU(H,P,TGT,DNDS,X,TIME,U,CINAME,SLNAME,
     1 MSNAME,NOEL,NODE,LCLOSE)
C
      INCLUDE 'ABA_PARAM.INC'
C
      CHARACTER*80 CINAME,SLNAME,MSNAME
C
      DIMENSION P(3),TGT(3,2),DNDS(3,2),X(3,2),TIME(2),U(6,2)

      user coding to define H, P, TGT, and DNDS

      RETURN
      END

Variables to be defined

H

Penetration of the point on the deforming structure into the surface of the rigid body, measured down the outward normal to the rigid surface. A negative value of H indicates that is outside the rigid surface. Even for a completely rigid surface, may appear to penetrate the surface during the iterations because the kinematic constraints are not fully satisfied until an increment converges.

P(3)

Position of the point on the surface of the rigid body closest to point on the surface of the deforming structure.

TGT(3,2)

Direction cosines of the two unit tangents to the surface, and , at point . For two-dimensional cases only the first two components of need be given since in this case ABAQUS/Standard assumes that is (0, 0, –1).

DNDS(3,2)

Rates of change of the surface normal, , at , with respect to distance measuring coordinates, and , along and . For two-dimensional cases only the first two entries in the first column of DNDS (, ) are required.

Variables passed in for information

X(K1,1)

Current coordinates of point on the surface of the deforming structure.

X(K1,2)

Current coordinates of the rigid body reference point.

TIME(1)

Value of step time at the end of the increment.

TIME(2)

Value of total time at the end of the increment.

U(K1,1)

Total displacement of point on the surface of the deforming structure.

U(K1,2)

Total displacement and rotation of the rigid body reference point; are the displacement components, are the rotation components. For two-dimensional cases the only nonzero rotation component is : U(4,2) and U(5,2) are both zero.

CINAME

User-specified surface interaction name, left justified. For user-defined contact elements it is either the element set name given for the interface definition or the optional name assigned to the interface definition.

SLNAME

Slave surface name. Passed in as blank if RSURFU is called for contact elements.

MSNAME

Master surface name. Passed in as blank if RSURFU is called for contact elements.

NOEL

Element label for contact elements. Passed in as zero if RSURFU is called for a contact pair.

NODE

Node number for point .

LCLOSE

Flag indicating contact status at the beginning of the increment. LCLOSE=1 indicates that is in contact (closed) at the beginning of the increment. LCLOSE=0 indicates that is not in contact (open) at the beginning of the increment. If LCLOSE=1, P, TGT and DNDS must be defined even if opens during this increment.

Example: Rigid punch

The input files for the following examples can be found in “RSURFU,” Section 4.1.9 of the ABAQUS Verification Manual.

Consider the punch shown in Figure 25.2.15–2.

Figure 25.2.15–2 Cross-section of a rigid punch.

It consists of a spherical head of radius

, smoothly merging into a conical section with cone angle

. The center of the sphere lies on the

-axis at

. We assume that the punch is being driven down the

-axis by a prescribed displacement at the rigid body reference node defined as a boundary condition. (This same surface could be defined directly as a three-dimensional surface of revolution, as described in “Defining analytical rigid surfaces,” Section 2.3.4. We define it here in RSURFU as an illustration.)

A point (slave node) on the surface of the deforming body will be associated with the spherical head or with the conical part of the punch, depending on whether it lies above or below the cone that passes through and the circle of intersection of the sphere and cone. Thus, define

in the three-dimensional case or

in the axisymmetric case. Then, if

, the point is associated with the spherical surface. Otherwise, it is associated with the cone (both cases are indicated in Figure 25.2.15–2).

Consider first the axisymmetric case. Then, for (the sphere) the overclosure is

where

The position of the point

on the rigid surface is (

), where

The tangent to the rigid surface at

The positive direction for

must be chosen so that the normal satisfies the right-hand rule with respect to

and

and points out of the rigid body. Also,

, so that

For (the conical surface) the clearance is

and the position of the point

on the rigid surface is

The surface tangent is

and there is no change in

with position, so that

The routine can then be coded as follows:

      SUBROUTINE RSURFU(H,P,TGT,DNDS,X,TIME,U,CINAME,SLNAME,
     1   MSNAME,NOEL,NODE,LCLOSE)
C     
      INCLUDE 'ABA_PARAM.INC'
C     
      CHARACTER*80 CINAME,SLNAME,MSNAME
      DIMENSION P(3),TGT(3,2),DNDS(3,2),X(3,2),TIME(2),U(6,2)
C     
C     DEFINE THE FOLLOWING QUANTITIES:
C     A = RADIUS 'A' OF THE SPHERICAL HEAD
C     SINA = SINE (CONE ANGLE ALPHA)
C     COSA = COSINE (CONE ANGLE ALPHA)
C     Z0 = ORIGINAL 'Z' COORDINATE OF POINT 'Q'
C     
      A=5.0
      SINA=0.5
      COSA=0.86602
      Z0=6.0
      ZQ=Z0 + U(2,2)
C     
C     TEST FOR SEGMENT
C     
      IF(X(1,1)*SINA/COSA.LT.ZQ-X(2,1))THEN
C     
C     SPHERE
C     
         B=SQRT(X(1,1)**2 + (X(2,1)-ZQ)**2)
         H=A-B
         COSB=X(1,1)/B
         SINB=(ZQ-X(2,1))/B
         P(1)=A*COSB
         P(2)=ZQ-A*SINB
         TGT(1,1)=-SINB
         TGT(2,1)=-COSB
         DNDS(1,1)=-SINB/A
         DNDS(2,1)=-COSB/A
      ELSE
C     CONE
         H=-X(1,1)*COSA+(X(2,1)-ZQ)*SINA+A
         P(1)=X(1,1) + H*COSA
         P(2)=X(2,1)- H*SINA
         TGT(1,1)=-SINA
         TGT(2,1)=-COSA
         DNDS(1,1)=0.
         DNDS(2,1)=0.
      END IF
      RETURN
      END

The above case can be directly extended to three dimensions. For this purpose we assume that the radial axis, , is in the global (–) plane, so that

For (the sphere), the overclosure is , where again

The point

on the rigid surface is (

), where

For

is not defined uniquely; in that case we arbitrarily choose

. We now need two tangents to the surface. The tangent

used in the axisymmetric case is now

and the orthogonal tangent is

Again, the positive directions of

and

are chosen so that

defines an outward normal to the surface. The distance measures on the surface are

so that

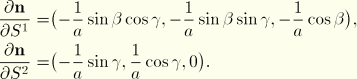
For the conical surface ( ), the surface separation is