17.2.4 Connector functions for coupled behavior

Products: ABAQUS/Standard ABAQUS/Explicit

References

Overview

This section describes how to define two special functions used to specify complex coupled behavior for a connector element in ABAQUS: derived components and potentials.

Connector derived components are user-specified component definitions based on a function of intrinsic (1 through 6) connector components of relative motion. They can be used:

to specify the friction-generating normal force in connectors as a complex combination of connector forces and moments, and
as an intermediate result in a connector potential function.

Connector potentials are user-defined functions of intrinsic components of relative motion or derived components. These functions can be quadratic, elliptical, or maximum norms. They can be used to define:

the yield function for connector coupled plasticity when several available components of relative motion are involved simultaneously,
the potential function for coupled user-defined friction when the slip direction is not aligned with an available component of relative motion,
a magnitude measure as a coupled function of connector forces or motions used to detect the initiation of damage in the connector, and
an effective motion measure as a coupled function of connector motions to drive damage evolution in the connector.

Defining derived components for connector elements

The definition of coupled behavior in connector elements beyond simple linear elasticity or damping often requires the definition of a resultant force involving several intrinsic (1 through 6) components or the definition of a “direction” not aligned with any of the intrinsic components. These user-defined resultants or directions are called derived components. The forces and motions associated with these derived components are functions of the forces and motions in the intrinsic relative components of motion in the connector element.

Consider the case of a SLOT connector for which frictional effects (see “Connector friction behavior,” Section 17.2.5) are defined in the only available component of relative motion (the 1-direction). The two constraints enforced by this connection type will produce two reaction forces ( and ), as shown in Figure 17.2.4–1. Both forces generate friction in the 1-direction in a coupled fashion.

Figure 17.2.4–1 Resultant contact force in a SLOT connector.

A reasonable estimate for the resulting contact force is

where

is the collection of connector forces and moments in the intrinsic components. The function

can be specified as a derived component.

Resultant forces that can be defined as derived components may take more complicated forms. Consider a BUSHING connection type for which a tensile (Mode I) damage mechanism with failure is to be specified in the 1-direction. You may wish to include the effects of the axial force and of the resultant of the “flexural” moments and in defining an overall resultant force in the axial direction upon which damage initiation (and failure) can be triggered, as shown in Figure 17.2.4–2.

Figure 17.2.4–2 Resultant axial force in a BUSHING connector.

One choice would be to define the resultant axial force as

where

is a geometric factor relating translations to rotations with units of one over length. The function

can be specified as a derived component.

A derived component can also be interpreted as a user-specified direction that is not aligned with the connector component directions. For example, if the motion-based damage with failure criterion in a CARTESIAN connection with elastic behavior does not align with the intrinsic component directions, the damage criterion can be defined in terms of a derived component representing a different direction, as shown in Figure 17.2.4–3.

Figure 17.2.4–3 User-defined direction in a CARTESIAN connector.

One possible choice for the direction could be

where

is the collection of connector relative motions in the components and

, and

can be interpreted as direction cosines (

). The function

can be specified as a derived component.

Functional form of the derived component

The functional form of a derived component in ABAQUS is quite general; you specify its exact form. The derived component is specified as a sum of terms

where

is a generic name for the connector intrinsic component values (such as forces,

, or motions,

is the

term in the sum, and

is the number of terms. The appropriate component values for

are selected depending on the context in which the derived component is used.

is also a summation of several contributions and can take one of the following two forms:

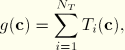
a norm
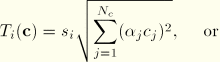
a direct sum

where

is the term's sign (plus or minus),

are scaling factors, and

is the

component of

Defining a derived component with only one term (N_T = 1)

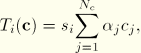
Connector derived components are identified by the names given to them. If one term () is sufficient to define the derived component , specify only one connector derived component definition.

Input File Usage:

*CONNECTOR DERIVED COMPONENT, NAME=derived_component_name

Defining a derived component containing multiple terms (N_T > 1)

If several terms (, , etc.) are needed in the overall definition of the derived component , you must specify connector derived component definitions with the same name to define the individual terms. All definitions with the same name will be summed together to produce the desired derived component . See the spot weld example below for an illustration.

Input File Usage:

*CONNECTOR DERIVED COMPONENT, NAME=derived_component_name
*CONNECTOR DERIVED COMPONENT, 
NAME=derived_component_name
...

Specifying a term in the derived component as a norm

By default, a derived component term is computed as the square root of the sum of the squares of each intrinsic component contribution. If the term has only one contribution (), the norm has the same meaning as the absolute value.

Input File Usage:

*CONNECTOR DERIVED COMPONENT, NAME=derived_component_name, OPERATOR=NORM (default)

For example, the following input can be used to define the

component discussed above:

*CONNECTOR DERIVED COMPONENT, NAME=axial
1
1.0, 
** 
*CONNECTOR DERIVED COMPONENT, NAME=axial
5, 6
, 
**

The axial derived component is .

Specifying a term in the derived component as a direct sum

Alternatively, you can choose to compute a derived component term as the direct sum of the intrinsic component contributions.

Input File Usage:

*CONNECTOR DERIVED COMPONENT, NAME=derived_component_name, OPERATOR=SUM

For example, the following input can be used to define the

component discussed above:

*CONNECTOR DERIVED COMPONENT, NAME=transf, OPERATOR=SUM
1, 2, 3
, , 
**

The transf derived component is .

Specifying the sign of a term

You can specify whether the sign of a derived component term should be positive or negative.

Input File Usage:	Use one of the following options:
	CONNECTOR DERIVED COMPONENT, NAME=derived_component_name, SIGN=POSITIVE (default) CONNECTOR DERIVED COMPONENT, NAME=derived_component_name, SIGN=NEGATIVE

Defining the derived component contributions to depend on local directions

The scaling factors used in the definition of the derived component can depend on the relative positions or constitutive displacements/rotations in several component directions, as described in “Defining connector properties to depend on local directions” in “Connector behavior,” Section 17.2.1. See the first example in “Connector friction behavior,” Section 17.2.5, for an illustration.

Input File Usage:

Use the following option to define a connector derived component that depends on components of relative position:

*CONNECTOR DERIVED COMPONENT, 
INDEPENDENT COMPONENTS=POSITION

Use the following option to define a connector derived component that depends on components of constitutive displacements or rotations:

*CONNECTOR DERIVED COMPONENT, 
INDEPENDENT COMPONENTS=CONSTITUTIVE MOTION

Requirements for constructing a derived component used in plasticity or friction definitions

When a derived component is used to construct the yield function for a plasticity or friction definition, the following simple requirements must be satisfied:

All terms of a derived component must be of the same type (see “Functional form of the derived component”); norm-type terms (-type) cannot be mixed with direct sum-type terms (-type) in the same derived component definition.
If all terms are norm-type terms, the sign of each term must be positive (the default).

Example: spot weld

The spot weld shown in Figure 17.2.4–4 is subjected to loading in the -direction.

Figure 17.2.4–4 Loading of a spot weld connection.

The connector chosen to model the spot weld has six available components of relative motion: three translations (components 1–3) and three rotations (components 4–6). You have chosen this connection type because you are modeling a general deformation state. However, you would like to define inelastic behavior in the connection in terms of a normal and a shear force since experimental data are available in this format.

Figure 17.2.4–5 Spot weld connection: derived component definitions.

Therefore, you want to derive the normal and shear components of the force, for example, as follows:

In these equations

and

have units of length; their interpretation is relatively straightforward if you consider the spot weld as a short beam with the axis along the spot weld axis (1-direction). If the average cross-section area of the spot weld is

and the beam's second moment of inertia about this axis is

can be interpreted as the ratio

. Furthermore, if the cross-section is considered to be circular,

becomes equal to 1/4 of the spot weld radius. In all cases

can be taken to be

To define , you would specify the following two connector derived component definitions, each with the same name:

*PARAMETER
=12.27
=19.63
=
=


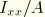
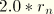
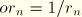
*CONNECTOR DERIVED COMPONENT, NAME=normal
1
1.0
*CONNECTOR DERIVED COMPONENT, NAME=normal
5, 6
,

The

symbols denote that

is specified using a parameter definition. The normal force derived component

is defined as the sum of two terms,

. The first connector derived component defines the first term

, while the second defines the second term

Similarly, to define , you would specify the following two connector derived component definitions for the component shear:

*CONNECTOR DERIVED COMPONENT, NAME=shear
4

*CONNECTOR DERIVED COMPONENT, NAME=shear
2, 3
1.0, 1.0

Defining connector potentials

Connector potentials are user-defined mathematical functions that represent yield surfaces, limiting surfaces, or magnitude measures in the space spanned by the components of relative motion in the connector. The functions can be quadratic, general elliptical, or maximum norms. The connector potential does not define a connector behavior by itself; instead, it is used to define the following coupled connector behaviors:

friction,
plasticity, or
damage.

Consider the case of a SLIDE-PLANE connection in which frictional sliding occurs in the connection plane, as shown in Figure 17.2.4–6.

Figure 17.2.4–6 Friction in the SLIDE-PLANE connection.

The function governing the stick-slip frictional behavior (see “Connector friction behavior,” Section 17.2.5) can be written as

where

is the connector potential defining the pseudo-yield function (the magnitude of the frictional tangential tractions in the connector in a direction tangent to the connection plane on which contact occurs),

is the friction-producing normal (contact) force, and

is the friction coefficient. Frictional stick occurs if

, and sliding occurs if

. In this case the potential can be defined as the magnitude of the frictional tangential tractions,

Connector potentials can also be useful in defining connector damage with a force-based coupled damage initiation criterion. For example, in a connection type with six available components of relative motion you could define a potential

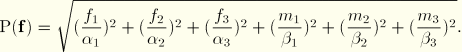
Damage (with failure) can be initiated when the value of the potential

is greater than a user-specified limiting value (usually 1.0).

Connector potentials can take more complicated forms. Assume that coupled plasticity is to be defined in a spot weld, in which case a plastic yield criterion can be defined as

where

is the connector potential defining the yield function and

is the yield force/moment. The potential could be defined as

where

and

could be the named derived components normal and shear defined in the example in “Defining derived components for connector elements” above.

Functional form of the potential

The functional form of the potential in ABAQUS is quite general; you specify its exact form. The potential is specified as one of the following direct functions of several contributions:

a quadratic form

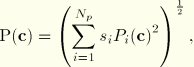
a general elliptical form

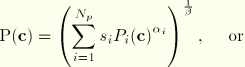
a maximum form

where

is a generic name for the connector intrinsic component values (such as forces,

, or motions,

is the

contribution to the potential,

is the number of contributions,

and

are positive exponents (defaults

2.0,

), and

is the overall sign of the contribution (1.0 – default, or –1.0). The appropriate component values for

are selected depending on the context in which the potential is used in. The positive exponents (

) and the sign

should be chosen such that the contribution

yields a real number.

is a direct function of either an intrinsic connector component (1 through 6) or a derived connector component. Since derived components are ultimately a function of intrinsic components (see “Defining derived components for connector elements”), the contribution is ultimately a function of . is defined as

where

is the function used to generate the contribution:

absolute value (default, ),

Macauley bracket (), or

identity ();

is the value of the identified component (intrinsic or derived);

is a shift factor (default 0.0); and

is a scaling factor (default 1.0).

The function

can be the identity function only if

Defining the potential as a quadratic or general elliptical form

To define a general elliptical form of the potential, you must specify the exponent . You can also define the exponents if they are different from the default specified value of the exponent . To define a quadratic form of the potential, you can omit the exponent since its default value is 2.0.

Input File Usage:

Use the following option to define a quadratic form of the potential:

*CONNECTOR POTENTIAL
component name or number, ,  , , , 
...

Use the following option to define a general elliptical form of the potential:

*CONNECTOR POTENTIAL, OPERATOR=SUM,  EXPONENT=
component name or number, , , , , 
...

Each data line defines one contribution to the potential, . The function can be ABS (absolute value and the default), MACAULEY (Macauley bracket), or NONE (identity).

Defining the potential as a maximum form

Alternatively, you can define the potential as a maximum form.

Input File Usage:	CONNECTOR POTENTIAL, OPERATOR=MAX component name or number*, , , , , ...
	Each data line defines one contribution to the potential, . The function can be ABS (absolute value and the default), MACAULEY (Macauley bracket), or NONE (identity).

Requirements for constructing a potential used in plasticity or friction definitions

The connector potential, , can be defined using intrinsic components of relative motion, derived components, or both. A particular contribution to the potential may be one of the following two types:

A norm-type contribution () defined using the absolute value or the Macauley bracket functions or using a norm-type derived component, (see “Requirements for constructing a derived component used in plasticity or friction definitions”) with any of the available functions.
A sum-type contribution () defined using an intrinsic component of relative motion or a derived component of type (see “Requirements for constructing a derived component used in plasticity or friction definitions”) together with the identity function.

When used in the context of connector plasticity or connector friction, the potential must be constructed such that the following requirements are satisfied:

All contributions to the potential must be of the same type. Mixed and contributions are not allowed in the same potential definition.
If all terms are -type terms, the sign of each term must be positive (the default).
The positive exponents and cannot be smaller than 1.0 and must be equal (the default).

Example: spot weld

Referring to the spot weld shown in Figure 17.2.4–5 and the yield function defined above, you would define this potential using the derived components normal and shear with the following input:

*PARAMETER
=0.02
=0.05
=1.5
*CONNECTOR POTENTIAL, EXPONENT=
normal, , , MACAULEY
shear, , , ABS