
Products: ABAQUS/Standard ABAQUS/Explicit ABAQUS/CAE

The time domain viscoelastic material model:
describes isotropic rate-dependent material behavior for materials in which dissipative losses primarily caused by “viscous” (internal damping) effects must be modeled in the time domain;
assumes that the shear (deviatoric) and volumetric behaviors are independent in multiaxial stress states (except when used for an elastomeric foam);
can be used only in conjunction with “Linear elastic behavior,” Section 10.2.1; “Hyperelastic behavior,” Section 10.5.1; or “Elastomeric foam behavior,” Section 10.5.2, to define the elastic material properties;
is active only during a transient static analysis (“Quasi-static analysis,” Section 6.2.5), a transient implicit dynamic analysis (“Implicit dynamic analysis using direct integration,” Section 6.3.2), an explicit dynamic analysis (“Explicit dynamic analysis,” Section 6.3.3), a steady-state transport analysis (“Steady-state transport analysis,” Section 6.4.1), a fully coupled temperature-displacement analysis (“Fully coupled thermal-stress analysis,” Section 6.5.4), or a transient (consolidation) coupled pore fluid diffusion and stress analysis (“Coupled pore fluid diffusion and stress analysis,” Section 6.7.1);
can be used in large-strain problems; and
can be calibrated using time-dependent creep test data, time-dependent relaxation test data, or frequency-dependent cyclic test data.

Time domain viscoelasticity is available in ABAQUS for small-strain applications where the rate-independent elastic response can be defined with a linear elastic material model and for large-strain applications where the rate-independent elastic response must be defined with a hyperelastic or hyperfoam material model.
Consider a shear test at small strain, in which a time varying shear strain, ![]() , is applied to the material. The response is the shear stress
, is applied to the material. The response is the shear stress ![]() . The viscoelastic material model defines
. The viscoelastic material model defines ![]() as
as
![]()
![]()
The shear relaxation modulus can be written in dimensionless form:
![]()
![]()
The equation for the stress can be transformed by using integration by parts:
![]()
![]()
In the above equation the instantaneous stress, ![]() , applied at time
, applied at time ![]() influences the stress,
influences the stress, ![]() , at time
, at time ![]() . Therefore, to create a proper finite-strain formulation, it is necessary to map the stress that existed in the configuration at time
. Therefore, to create a proper finite-strain formulation, it is necessary to map the stress that existed in the configuration at time ![]() into the configuration at time
into the configuration at time ![]() . In ABAQUS this is done by means of a mixed “push-forward” transformation with the relative deformation gradient
. In ABAQUS this is done by means of a mixed “push-forward” transformation with the relative deformation gradient ![]() :
:
![]()
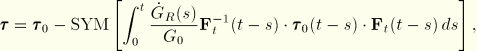
The finite-strain theory is described in more detail in “Finite-strain viscoelasticity,” Section 4.8.2 of the ABAQUS Theory Manual.

The volumetric behavior can be written in a form that is similar to the shear behavior:
![]()
The above expansion applies to small as well as finite strain since the volume strains are generally small and there is no need to map the pressure from time ![]() to time
to time ![]() .
.

The effect of temperature, ![]() , on the material behavior is introduced through the dependence of the instantaneous stress,
, on the material behavior is introduced through the dependence of the instantaneous stress, ![]() , on temperature and through a reduced time concept. The expression for the linear-elastic shear stress is rewritten as
, on temperature and through a reduced time concept. The expression for the linear-elastic shear stress is rewritten as
![]()
![]()
![]()
The reduced time concept is also used for the volumetric behavior and the large-strain formulation. For additional information on the WLF equation, see “Viscoelasticity,” Section 4.8.1 of the ABAQUS Theory Manual.

ABAQUS assumes that the viscoelastic material is defined by a Prony series expansion of the dimensionless relaxation modulus:
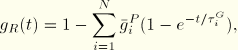
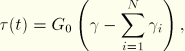
![]()
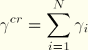
A similar Prony series expansion is used for the volumetric response, which is valid for both small- and finite-strain applications:
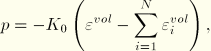
![]()
The Prony series expansion, in combination with the finite-strain expression for the shear stress, produces the following large-strain shear model:
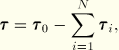
![]()
If the instantaneous material behavior is defined by linear elasticity or hyperelasticity, the bulk and shear behavior can be defined independently. However, if the instantaneous behavior is defined by the hyperfoam model, the deviatoric and volumetric constitutive behavior are coupled and it is necessary to use the same relaxation data for both behaviors.
In all of the above expressions temperature dependence is readily introduced by replacing ![]() by
by ![]() and
and ![]() by
by ![]() .
.

The above equations are used to model the time-dependent shear and volumetric behavior of a viscoelastic material. The relaxation parameters can be defined in one of four ways: direct specification of the Prony series parameters, inclusion of creep test data, inclusion of relaxation test data, or inclusion of frequency-dependent data obtained from sinusoidal oscillation experiments. Temperature effects are included in the same manner regardless of the method used to define the viscoelastic material.
ABAQUS/CAE allows you to evaluate the behavior of viscoelastic materials by automatically creating creep and relaxation response curves based on experimental test data or coefficients. A viscoelastic material can be evaluated only if it is defined in the time domain and includes hyperelastic and/or elastic material data. See “Evaluating hyperelastic and viscoelastic material behavior,” Section 12.4.6 of the ABAQUS/CAE User's Manual.
The Prony series parameters ![]() ,
, ![]() , and
, and ![]() can be defined directly for each term in the Prony series. There is no restriction on the number of terms that can be used. If a relaxation time is associated with only one of the two moduli, leave the other one blank or enter a zero. The data should be given in ascending order of the relaxation time. The number of lines of data given defines the number of terms in the Prony series,
can be defined directly for each term in the Prony series. There is no restriction on the number of terms that can be used. If a relaxation time is associated with only one of the two moduli, leave the other one blank or enter a zero. The data should be given in ascending order of the relaxation time. The number of lines of data given defines the number of terms in the Prony series, ![]() . If this model is used in conjunction with the hyperfoam material model, the two modulus ratios have to be the same (
. If this model is used in conjunction with the hyperfoam material model, the two modulus ratios have to be the same (![]() ).
).
| Input File Usage: | *VISCOELASTIC, TIME=PRONY |
| The data line is repeated as often as needed to define the first, second, third, etc. terms in the Prony series. |
| ABAQUS/CAE Usage: | Property module: material editor: Mechanical |
| Enter as many rows of data in the table as needed to define the first, second, third, etc. terms in the Prony series. |
If creep test data are specified, ABAQUS will calculate the terms in the Prony series automatically. The normalized shear and bulk compliances are defined as
![]()
The creep data are converted to relaxation data through the convolution integrals
![]()
The shear test data and volumetric test data can be used consecutively to define the normalized shear and bulk compliances as functions of time. A separate least-squares fit is performed on each data set; and the two derived sets of Prony series parameters, ![]() and
and ![]() , are merged into one set of parameters,
, are merged into one set of parameters, ![]() .
.
| Input File Usage: | Use the following three options. The first option is required. Only one of the second and third options is required. |
*VISCOELASTIC, TIME=CREEP TEST DATA *SHEAR TEST DATA *VOLUMETRIC TEST DATA |
| ABAQUS/CAE Usage: | Property module: material editor: Mechanical |
| In addition, select one or both of the following: Test Data |
Alternatively, the combined test data can be used to specify the normalized shear and bulk compliances simultaneously as functions of time. A single least-squares fit is performed on the combined set of test data to determine one set of Prony series parameters, ![]() .
.
| Input File Usage: | Use both of the following options: |
*VISCOELASTIC, TIME=CREEP TEST DATA *COMBINED TEST DATA |
| ABAQUS/CAE Usage: | Property module: material editor: Mechanical |
As with creep test data, ABAQUS will calculate the Prony series parameters automatically from relaxation test data.
Again, the shear test data and volumetric test data can be used consecutively to define the relaxation moduli as functions of time. A separate nonlinear least-squares fit is performed on each data set; and the two derived sets of Prony series parameters, ![]() and
and ![]() , are merged into one set of parameters,
, are merged into one set of parameters, ![]() .
.
| Input File Usage: | Use the following three options. The first option is required. Only one of the second and third options is required. |
*VISCOELASTIC, TIME=RELAXATION TEST DATA *SHEAR TEST DATA *VOLUMETRIC TEST DATA |
| ABAQUS/CAE Usage: | Property module: material editor: Mechanical |
| In addition, select one or both of the following: Test Data |
Alternatively, the combined test data can be used to specify the relaxation moduli simultaneously as functions of time. A single least-squares fit is performed on the combined set of test data to determine one set of Prony series parameters, ![]() .
.
| Input File Usage: | Use both of the following options: |
*VISCOELASTIC, TIME=RELAXATION TEST DATA *COMBINED TEST DATA |
| ABAQUS/CAE Usage: | Property module: material editor: Mechanical |
The Prony series terms can also be calibrated using frequency-dependent test data. In this case ABAQUS uses analytical expressions that relate the Prony series relaxation functions to the storage and loss moduli. The expressions for the shear moduli, obtained by converting the Prony series terms from the time domain to the frequency domain by making use of Fourier transforms, can be written as follows:
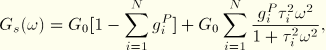
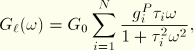
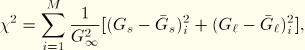
The frequency domain data are defined in tabular form by giving the real and imaginary parts of ![]() and
and ![]() —where
—where ![]() is the circular frequency—as functions of frequency in cycles per time.
is the circular frequency—as functions of frequency in cycles per time. ![]() is the Fourier transform of the nondimensional shear relaxation function
is the Fourier transform of the nondimensional shear relaxation function ![]() . Given the frequency-dependent storage and loss moduli
. Given the frequency-dependent storage and loss moduli ![]() ,
, ![]() ,
, ![]() , and
, and ![]() , the real and imaginary parts of
, the real and imaginary parts of ![]() and
and ![]() are then given as
are then given as
![]()
| Input File Usage: | *VISCOELASTIC, TIME=FREQUENCY DATA |
| ABAQUS/CAE Usage: | Property module: material editor: Mechanical |
You can specify two optional parameters related to the calibration of Prony series parameters for viscoelastic materials: the error tolerance and ![]() . The error tolerance is the allowable average root-mean-square error of data points in the least-squares fit, and its default value is 0.01.
. The error tolerance is the allowable average root-mean-square error of data points in the least-squares fit, and its default value is 0.01. ![]() is the maximum number of terms
is the maximum number of terms ![]() in the Prony series, and its default (and maximum) value is 13. ABAQUS will perform the least-squares fit from
in the Prony series, and its default (and maximum) value is 13. ABAQUS will perform the least-squares fit from ![]() to
to ![]() until convergence is achieved for the lowest
until convergence is achieved for the lowest ![]() with respect to the error tolerance.
with respect to the error tolerance.
The following are some guidelines for determining the number of terms in the Prony series from test data. Based on these guidelines, you can choose ![]() .
.
There should be enough data pairs for determining all the parameters in the Prony series terms. Thus, assuming that ![]() is the number of Prony series terms, there should be a total of at least
is the number of Prony series terms, there should be a total of at least ![]() data points in shear test data,
data points in shear test data, ![]() data points in volumetric test data,
data points in volumetric test data, ![]() data points in combined test data, and
data points in combined test data, and ![]() data points in the frequency domain.
data points in the frequency domain.
The number of terms in the Prony series should be typically not more than the number of logarithmic “decades” spanned by the test data. The number of logarithmic “decades” is defined as ![]() , where
, where ![]() and
and ![]() are the maximum and minimum time in the test data, respectively.
are the maximum and minimum time in the test data, respectively.
| Input File Usage: | *VISCOELASTIC, ERRTOL=error_tolerance, NMAX= |
| ABAQUS/CAE Usage: | Property module: material editor: Mechanical |
Regardless of the method used to define the viscoelastic behavior, thermo-rheologically simple temperature effects can be included by specifying the method used to define the shift function. The shift function can be defined by the Williams-Landell-Ferry (WLF) approximation.
| Input File Usage: | In ABAQUS/Standard use the following option: |
*TRS, DEFINITION=WLF In ABAQUS/Explicit use the following option: *TRS |
| ABAQUS/CAE Usage: | Property module: material editor: Mechanical |
In ABAQUS/Standard the shift function can alternatively be specified in user subroutine UTRS (“UTRS,” Section 25.2.42).
| Input File Usage: | *TRS, DEFINITION=USER |
| ABAQUS/CAE Usage: | Property module: material editor: Mechanical |

In all cases elastic moduli must be specified to define the rate-independent part of the material behavior. Small-strain linear elastic behavior is defined by an elastic material model (“Linear elastic behavior,” Section 10.2.1), and large-deformation behavior is defined by a hyperelastic (“Hyperelastic behavior,” Section 10.5.1) or hyperfoam (“Elastomeric foam behavior,” Section 10.5.2) material model. The rate-independent elasticity for any of these models can be defined in terms of either instantaneous elastic moduli or long-term elastic moduli. The choice of defining the elasticity in terms of instantaneous or long-term moduli is a matter of convenience only; it does not have an effect on the solution.
The effective relaxation moduli are obtained by multiplying the instantaneous elastic moduli with the dimensionless relaxation functions as described below.
For linear elastic material behavior
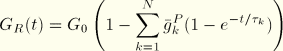
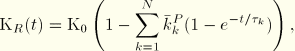
If long-term elastic moduli are defined, the instantaneous moduli are determined from
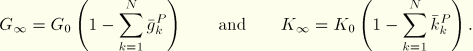
For hyperelastic material behavior the relaxation coefficients are applied either to the constants that define the energy function or directly to the energy function. For the polynomial function and its particular cases (reduced polynomial, Mooney-Rivlin, neo-Hookean, and Yeoh)
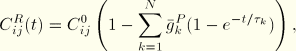
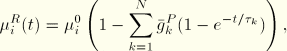
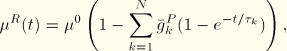
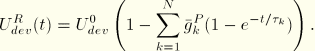
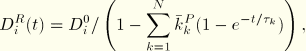
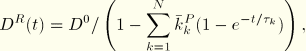
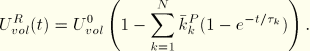
If long-term elastic moduli are defined, the instantaneous moduli are determined from
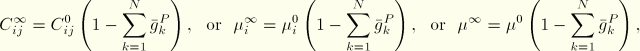
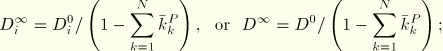
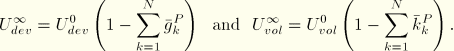
For elastomeric foam material behavior the instantaneous shear and bulk relaxation coefficients are assumed to be equal and are applied to the material constants ![]() in the energy function:
in the energy function:
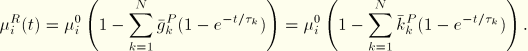
If only the shear relaxation coefficients are specified, the bulk relaxation coefficients are set equal to the shear relaxation coefficients and vice versa. If both shear and bulk relaxation coefficients are specified and they are unequal, ABAQUS issues an error message.
If long-term elastic moduli are defined, the instantaneous moduli are determined from
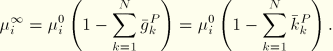

The time-domain viscoelastic material model is active during the following procedures:
transient static analysis (“Quasi-static analysis,” Section 6.2.5),
transient implicit dynamic analysis (“Implicit dynamic analysis using direct integration,” Section 6.3.2),
explicit dynamic analysis (“Explicit dynamic analysis,” Section 6.3.3),
steady-state transport analysis (“Steady-state transport analysis,” Section 6.4.1),
fully coupled temperature-displacement analysis (“Fully coupled thermal-stress analysis,” Section 6.5.4), and
transient (consolidation) coupled pore fluid diffusion and stress analysis (“Coupled pore fluid diffusion and stress analysis,” Section 6.7.1).
Viscoelastic material response is always ignored in a static analysis. It can also be ignored in a coupled temperature-displacement analysis or in a soils consolidation analysis by specifying that no creep or viscoelastic response is occurring during the step even if creep or viscoelastic material properties are defined (see “Fully coupled thermal-stress analysis,” Section 6.5.4, or “Coupled pore fluid diffusion and stress analysis,” Section 6.7.1). In these cases it is assumed that the loading is applied instantaneously, so that the resulting response corresponds to an elastic solution based on instantaneous elastic moduli.
ABAQUS/Standard also provides the option to obtain the fully relaxed long-term elastic solution directly in a static or steady-state transport analysis without having to perform a transient analysis. The long-term value is used for this purpose. The viscous damping stresses (the internal stresses associated with each of the Prony-series terms) are increased gradually from their values at the beginning of the step to their long-term values at the end of the step if the long-term value is specified.

The viscoelastic material model must be combined with an elastic material model. It is used with the isotropic linear elasticity model (“Linear elastic behavior,” Section 10.2.1) to define classical, linear, small-strain, viscoelastic behavior or with the hyperelastic (“Hyperelastic behavior,” Section 10.5.1) or hyperfoam (“Elastomeric foam behavior,” Section 10.5.2) models to define large-deformation, nonlinear, viscoelastic behavior. The elastic properties defined for these models can be temperature dependent.
Viscoelasticity cannot be combined with any of the plasticity models or with the Mullins effect material model. See “Combining material behaviors,” Section 9.1.3, for more details.

The time domain viscoelastic material model can be used with any stress/displacement or coupled temperature-displacement element in ABAQUS.

In addition to the standard output identifiers available in ABAQUS (“ABAQUS/Standard output variable identifiers,” Section 4.2.1, and “ABAQUS/Explicit output variable identifiers,” Section 4.2.2), the following variables have special meaning in ABAQUS/Standard if viscoelasticity is defined:
EE | Elastic strain corresponding to the stress state at time |
CE | Equivalent creep strain defined as the difference between the total strain and the elastic strain. |
For the case of large-strain viscoelasticity, ABAQUS/Explicit does not perform the computation of the viscous dissipation for performance reasons. Instead, the contribution of viscous dissipation is included in the strain energy output, SENER; and CENER is output as zero. Consequently, special care must be exercised when interpreting strain energy results of large-strain viscoelastic materials in ABAQUS/Explicit since they include viscous dissipation effects.