Products: ABAQUS/Standard ABAQUS/CAE
The frequency domain viscoelastic material model:
describes frequency-dependent material behavior in small steady-state harmonic oscillations for those materials in which dissipative losses caused by “viscous” (internal damping) effects must be modeled in the frequency domain;
assumes that the shear (deviatoric) and volumetric behaviors are independent in multiaxial stress states;
can be used in large-strain problems;
is isotropic and linear;
can be used only in conjunction with either “Linear elastic behavior,” Section 10.2.1, or “Hyperelastic behavior,” Section 10.5.1, to define the long-term elastic material properties; and
is active only during the direct-solution steady-state dynamic procedure (“Direct-solution steady-state dynamic analysis,” Section 6.3.4).
Consider a shear test at small strain, in which a harmonically varying shear strain 
is applied:
is the amplitude, 
, 
is the circular frequency, and 
is time. We assume that the specimen has been oscillating for a very long time so that a steady-state solution is obtained. The solution for the shear stress then has the form 
and 
are the shear storage and loss moduli. These moduli can be expressed in terms of the (complex) Fourier transform 
of the nondimensional shear relaxation function 
: 
is the time-dependent shear relaxation modulus, 
and 
are the real and imaginary parts of , and 
is the long-term shear modulus. See “Frequency domain viscoelasticity,” Section 4.8.3 of the ABAQUS Theory Manual, for details.The above equation states that the material responds to steady-state harmonic strain with a stress of magnitude that is in phase with the strain and a stress of magnitude that lags the excitation by 
. Hence, we can regard the factor
Measurements of 
and 
as functions of frequency in an experiment can, thus, be used to define and and, thus, and as functions of frequency.
In multiaxial stress states ABAQUS/Standard assumes that the frequency dependence of the shear (deviatoric) and volumetric behaviors are independent. The volumetric behavior is defined by the bulk storage and loss moduli 
and 
. Similar to the shear moduli, these moduli can also be expressed in terms of the (complex) Fourier transform 
of the nondimensional bulk relaxation function 
:
is the long-term elastic bulk modulus.The linearized vibrations can also be associated with an elastomeric material whose long-term (elastic) response is nonlinear and involves finite strains (a hyperelastic material). We can retain the simplicity of the steady-state small-amplitude vibration response analysis in this case by assuming that the linear expression for the shear stress still governs the system, except that now the long-term shear modulus can vary with the amount of static prestrain 
:
of the relaxation function, is not affected by the magnitude of the prestrain. Thus, strain and frequency effects are separated, which is a reasonable approximation for many materials.The generalization of these concepts to arbitrary three-dimensional deformations is provided in ABAQUS/Standard by assuming that the frequency-dependent material behavior has two independent components: one associated with shear (deviatoric) straining and the other associated with volumetric straining. In the general case of a compressible material, the model is, therefore, defined for kinematically small perturbations about a predeformed state as
is the deviatoric stress, 
;
is the equivalent pressure stress, 
;
is the part of the stress increment caused by incremental straining (as distinct from the part of the stress increment caused by incremental rotation of the preexisting stress with respect to the coordinate system);
is the ratio of current to original volume;
is the (small) incremental deviatoric strain, 
;
is the deviatoric strain rate, 
;
is the (small) incremental volumetric strain, 
;
is the rate of volumetric strain, 
;
is the deviatoric tangent elasticity matrix of the material in its predeformed state (for example, 
is the tangent shear modulus of the prestrained material);
is the volumetric strain-rate/deviatoric stress-rate tangent elasticity matrix of the material in its predeformed state; and
is the tangent bulk modulus of the predeformed material.
For a fully incompressible material only the deviatoric terms in the first constitutive equation above remain and the viscoelastic behavior is completely defined by .
The dissipative part of the material behavior is defined by giving the real and imaginary parts of 
and 
(for compressible materials) as functions of frequency. The moduli can be defined as functions of the frequency in one of three ways: by a power law, by tabular input, or by a Prony series expression for the shear and bulk relaxation moduli.
The frequency dependence can be defined by the power law formulæ
and 
are real constants, 
and 
are complex constants, and 
is the frequency in cycles per time.| Input File Usage: | *VISCOELASTIC, FREQUENCY=FORMULA |
| ABAQUS/CAE Usage: | Property module: material editor: Mechanical |
The frequency domain response can alternatively be defined in tabular form by giving the real and imaginary parts of 
and 
—where is the circular frequency—as functions of frequency in cycles per time. Given the frequency-dependent storage and loss moduli 
, 
, , and , the real and imaginary parts of and are then given as
and are the long-term shear and bulk moduli determined from the elastic or hyperelastic properties.| Input File Usage: | *VISCOELASTIC, FREQUENCY=TABULAR |
| ABAQUS/CAE Usage: | Property module: material editor: Mechanical |
The frequency dependence can also be obtained from a time domain Prony series description of the dimensionless shear and bulk relaxation moduli:
, 
, 
, and 
, 
, are material constants. Using Fourier transforms, the expression for the time-dependent shear modulus can be written in the frequency domain as follows:
is the storage modulus, is the loss modulus, is the angular frequency, and is the number of terms in the Prony series. The expressions for the bulk moduli, and , are written analogously. ABAQUS/Standard will automatically perform the conversion from the time domain to the frequency domain. The Prony series parameters 
can be defined in one of three ways: direct specification of the Prony series parameters, inclusion of creep test data, or inclusion of relaxation test data. If creep test data or relaxation test data are specified, ABAQUS/Standard will determine the Prony series parameters in a nonlinear least-squares fit. 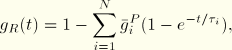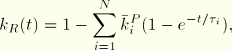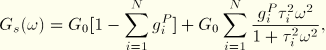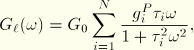A detailed description of the calibration of Prony series terms is provided in “Time domain viscoelasticity,” Section 10.7.1.For the test data you can specify the normalized shear and bulk data separately as functions of time or specify the normalized shear and bulk data simultaneously. A nonlinear least-squares fit is performed to determine the Prony series parameters, 
.
| Input File Usage: | Use one of the following options to specify Prony data, creep test data, or relaxation test data: |
*VISCOELASTIC, FREQUENCY=PRONY *VISCOELASTIC, FREQUENCY=CREEP TEST DATA *VISCOELASTIC, FREQUENCY=RELAXATION TEST DATA Use one or both of the following options to specify the normalized shear and bulk data separately as functions of time: *SHEAR TEST DATA *VOLUMETRIC TEST DATA Use the following option to specify the normalized shear and bulk data simultaneously: *COMBINED TEST DATA |
| ABAQUS/CAE Usage: | Property module: material editor: Mechanical |
| Use one or both of the following options to specify the normalized shear and bulk data separately as functions of time: Test Data Use the following option to specify the normalized shear and bulk data simultaneously: Test Data |
For some cases of small straining of isotropic viscoelastic materials, the material data are provided as frequency-dependent uniaxial storage and loss moduli, 
and 
, and bulk moduli, and . In that case the data must be converted to obtain the frequency-dependent shear storage and loss moduli and .
The complex shear modulus is obtained as a function of the complex uniaxial and bulk moduli with the expression
In all cases elastic moduli must be specified to define the rate-independent part of the material behavior. The elastic behavior is defined by an elastic, hyperelastic, or hyperfoam material model. Since the frequency domain viscoelastic material model is developed around the long-term elastic moduli, the rate-independent elasticity must be defined in terms of long-term elastic moduli. This implies that the response in any analysis procedure other than a direct-solution steady-state dynamic analysis (such as a static preloading analysis) corresponds to the fully relaxed long-term elastic solution.
The viscoelastic material model must be combined with the isotropic linear elasticity model to define classical, linear, small-strain, viscoelastic behavior. It is combined with the hyperelastic or hyperfoam model to define large-deformation, nonlinear, viscoelastic behavior. The long-term elastic properties defined for these models can be temperature dependent.
Viscoelasticity cannot be combined with any of the plasticity models. See “Combining material behaviors,” Section 9.1.3, for more details.
Elasticity
and 
. For this case the expressions for the shear moduli simplify to 
