
Products: ABAQUS/Standard ABAQUS/Explicit ABAQUS/CAE

The elastomeric foam material model:
is isotropic and nonlinear;
is valid for cellular solids whose porosity permits very large volumetric changes;
optionally allows the specification of energy dissipation and stress softening effects (see “Energy dissipation in elastomeric foams,” Section 10.6.2);
can deform elastically to large strains, up to 90% strain in compression; and
requires that geometric nonlinearity be accounted for during the analysis step (see “Procedures: overview,” Section 6.1.1, and “General and linear perturbation procedures,” Section 6.1.2), since it is intended for finite-strain applications.

Cellular solids are made up of interconnected networks of solid struts or plates that form the edges and faces of cells. Foams are made up of polyhedral cells that pack in three dimensions. The foam cells can be either open (e.g., sponge) or closed (e.g., flotation foam). Common examples of elastomeric foam materials are cellular polymers such as cushions, padding, and packaging materials that utilize the excellent energy absorption properties of foams: the energy absorbed by foams is substantially greater than that absorbed by ordinary stiff elastic materials for a certain stress level.
Another class of foam materials is crushable foams, which undergo permanent (plastic) deformation. Crushable foams are discussed in “Crushable foam plasticity models,” Section 11.3.5.
Foams are commonly loaded in compression. Figure 10.5.2–1 shows a typical compressive stress-strain curve.
Three stages can be distinguished during compression:At small strains (![]() 5%) the foam deforms in a linear elastic manner due to cell wall bending.
5%) the foam deforms in a linear elastic manner due to cell wall bending.
The next stage is a plateau of deformation at almost constant stress, caused by the elastic buckling of the columns or plates that make up the cell edges or walls. In closed cells the enclosed gas pressure and membrane stretching increase the level and slope of the plateau.
Finally, a region of densification occurs, where the cell walls crush together, resulting in a rapid increase of compressive stress. Ultimate compressive nominal strains of 0.7 to 0.9 are typical.
At small strains the foam deforms in a linear, elastic manner as a result of cell wall bending, similar to that in compression.
The cell walls rotate and align, resulting in rising stiffness. The walls are substantially aligned at a tensile strain of about ![]() . Further stretching results in increased axial strains in the walls.
. Further stretching results in increased axial strains in the walls.
The manufacture of foams often results in cells with different principal dimensions. This shape anisotropy results in different loading responses in different directions. However, the hyperfoam model does not take this kind of initial anisotropy into account.

In the elastomeric foam material model the elastic behavior of the foams is based on the strain energy function
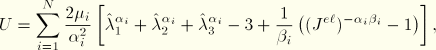
![]()
The coefficients ![]() are related to the initial shear modulus,
are related to the initial shear modulus, ![]() , by
, by
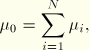
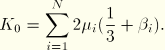
For each term in the energy function, the coefficient ![]() determines the degree of compressibility.
determines the degree of compressibility. ![]() is related to the Poisson's ratio,
is related to the Poisson's ratio, ![]() , by the expressions
, by the expressions
![]()

Only isotropic thermal expansion is permitted with the hyperfoam material model.
The elastic volume ratio, ![]() , relates the total volume ratio (current volume/reference volume),
, relates the total volume ratio (current volume/reference volume), ![]() , and the thermal volume ratio,
, and the thermal volume ratio, ![]() :
:
![]()
![]()

The response of the material is defined by the parameters in the strain energy function, ![]() ; these parameters must be determined to use the hyperfoam model. Two methods are provided for defining the material parameters: you can specify the hyperfoam material parameters directly or specify test data and allow ABAQUS to calculate the material parameters.
; these parameters must be determined to use the hyperfoam model. Two methods are provided for defining the material parameters: you can specify the hyperfoam material parameters directly or specify test data and allow ABAQUS to calculate the material parameters.
The elastic response of a viscoelastic material (“Time domain viscoelasticity,” Section 10.7.1) can be specified by defining either the instantaneous response or the long-term response of such a material. To define the instantaneous response, the experiments outlined in the “Experimental tests” section that follows have to be performed within time spans much shorter than the characteristic relaxation time of the material.
| Input File Usage: | *HYPERFOAM, MODULI=INSTANTANEOUS |
| ABAQUS/CAE Usage: | Property module: material editor: Mechanical |
If, on the other hand, the long-term elastic response is used, data from experiments have to be collected after time spans much longer than the characteristic relaxation time of the viscoelastic material. Long-term elastic response is the default elastic material behavior.
| Input File Usage: | *HYPERFOAM, MODULI=LONG TERM |
| ABAQUS/CAE Usage: | Property module: material editor: Mechanical |
When the parameters ![]() ,
, ![]() ,
, ![]() , and
, and ![]() are specified directly, they can be functions of temperature.
are specified directly, they can be functions of temperature.
The default value of ![]() is zero, which corresponds to an effective Poisson's ratio of zero. The incompressible limit corresponds to all
is zero, which corresponds to an effective Poisson's ratio of zero. The incompressible limit corresponds to all ![]() . However, this material model should not be used for approximately incompressible materials: use of the hyperelastic model (“Hyperelastic behavior,” Section 10.5.1) is recommended if the effective Poisson's ratio
. However, this material model should not be used for approximately incompressible materials: use of the hyperelastic model (“Hyperelastic behavior,” Section 10.5.1) is recommended if the effective Poisson's ratio ![]() .
.
| Input File Usage: | *HYPERFOAM, N=n ( |
| ABAQUS/CAE Usage: | Property module: material editor: Mechanical |
The value of ![]() and the experimental stress-strain data can be specified for up to five simple tests: uniaxial, equibiaxial, simple shear, planar, and volumetric. ABAQUS contains a capability for obtaining the
and the experimental stress-strain data can be specified for up to five simple tests: uniaxial, equibiaxial, simple shear, planar, and volumetric. ABAQUS contains a capability for obtaining the ![]() ,
, ![]() , and
, and ![]() for the hyperfoam model with up to six terms (
for the hyperfoam model with up to six terms (![]() =6) directly from test data. Poisson effects can be included either by means of a constant Poisson's ratio or through specification of volumetric test data and/or lateral strains in the other test data.
=6) directly from test data. Poisson effects can be included either by means of a constant Poisson's ratio or through specification of volumetric test data and/or lateral strains in the other test data.
It is important to recognize that the properties of foam materials can vary significantly from one batch to another. Therefore, all of the experiments should be performed on specimens taken from the same batch of material.
This method does not allow the properties to be temperature dependent.
As many data points as required can be entered from each test. ABAQUS will then compute ![]() ,
, ![]() , and, if necessary,
, and, if necessary, ![]() . The technique uses a least squares fit to the experimental data so that the relative error in the nominal stress is minimized.
. The technique uses a least squares fit to the experimental data so that the relative error in the nominal stress is minimized.
It is recommended that data from the uniaxial, biaxial, and simple shear tests (on samples taken from the same piece of material) be included and that the data points cover the range of nominal strains expected to arise in the actual loading. The planar and volumetric tests are optional.
For all tests the strain data, including the lateral strain data, should be given as nominal strain values (change in length per unit of original length). For the uniaxial, equibiaxial, simple shear, and planar tests, stress data are given as nominal stress values (force per unit of original cross-sectional area). The tests allow for both compression and tension data; compressive stresses and strains should be entered as negative values. For the volumetric tests the stress data are given as pressure values.
| Input File Usage: | Use the first option to define an effective Poisson's ratio ( |
*HYPERFOAM, N=n, POISSON= In addition, use at least one and up to five of these additional options to give the experimental stress-strain data (see “Experimental tests” below): *UNIAXIAL TEST DATA *BIAXIAL TEST DATA *PLANAR TEST DATA *SIMPLE SHEAR TEST DATA *VOLUMETRIC TEST DATA |
| ABAQUS/CAE Usage: | Property module: material editor: Mechanical |
| In addition, use at least one and up to five of the suboptions to give the experimental stress-strain data (see “Experimental tests” below): Suboptions Suboptions Suboptions Suboptions Suboptions |

For a homogeneous material, homogeneous deformation modes suffice to characterize the material parameters. ABAQUS accepts test data from the following deformation modes:
Uniaxial tension and compression
Equibiaxial tension and compression
Planar tension and compression (pure shear)
Simple shear
Volumetric tension and compression
![]()
The deformation gradient, expressed in the principal directions of stretch, is
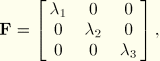
The three deformation modes use a single form of the nominal stress-stretch relation,
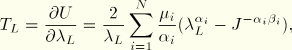
In uniaxial mode ![]() ,
, ![]() , and
, and ![]() .
.
| Input File Usage: | *UNIAXIAL TEST DATA |
| ABAQUS/CAE Usage: | Property module: material editor: Mechanical |
In equibiaxial mode ![]() and
and ![]() .
.
| Input File Usage: | *BIAXIAL TEST DATA |
| ABAQUS/CAE Usage: | Property module: material editor: Mechanical |
In planar mode ![]() ,
, ![]() , and
, and ![]() . Planar test data must be augmented by either uniaxial or biaxial test data.
. Planar test data must be augmented by either uniaxial or biaxial test data.
| Input File Usage: | *PLANAR TEST DATA |
| ABAQUS/CAE Usage: | Property module: material editor: Mechanical |
Simple shear is described by the deformation gradient
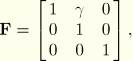
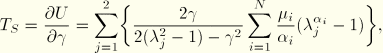
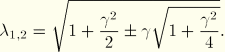
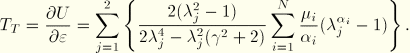
| Input File Usage: | *SIMPLE SHEAR TEST DATA |
| ABAQUS/CAE Usage: | Property module: material editor: Mechanical |
The deformation gradient, ![]() , is the same for volumetric tests as for uniaxial tests. The volumetric deformation mode consists of all principal stretches being equal;
, is the same for volumetric tests as for uniaxial tests. The volumetric deformation mode consists of all principal stretches being equal;
![]()
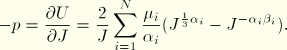
A volumetric compression test is illustrated in Figure 10.5.2–4. The pressure exerted on the foam specimen is the hydrostatic pressure of the fluid, and the decrease in the specimen volume is equal to the additional fluid entering the pressure chamber. The specimen is sealed against fluid penetration.
| Input File Usage: | *VOLUMETRIC TEST DATA |
| ABAQUS/CAE Usage: | Property module: material editor: Mechanical |

For small strains (![]() 5%) foams behave similarly for both compression and tension. However, at large strains the deformation mechanisms differ for compression (buckling and crushing) and tension (alignment and stretching). Therefore, accurate hyperfoam modeling requires that the experimental data used to define the material parameters correspond to the dominant deformation modes of the problem being analyzed. If compression dominates, the pertinent tests are:
5%) foams behave similarly for both compression and tension. However, at large strains the deformation mechanisms differ for compression (buckling and crushing) and tension (alignment and stretching). Therefore, accurate hyperfoam modeling requires that the experimental data used to define the material parameters correspond to the dominant deformation modes of the problem being analyzed. If compression dominates, the pertinent tests are:
Uniaxial compression
Simple shear
Planar compression (if Poisson's ratio ![]() )
)
Volumetric compression (if Poisson's ratio ![]() )
)
Uniaxial tension
Simple shear
Biaxial tension (if Poisson's ratio ![]() )
)
Planar tension (if Poisson's ratio ![]() )
)

Once the elastomeric foam constants are determined, the behavior of the hyperfoam model in ABAQUS is established. However, the quality of this behavior must be assessed: the prediction of material behavior under different deformation modes must be compared against the experimental data. You must judge whether the elastomeric foam constants determined by ABAQUS are acceptable, based on the correlation between the ABAQUS predictions and the experimental data. Single-element test cases can be used to calculate the nominal stress–nominal strain response of the material model.
See “Fitting of elastomeric foam test data,” Section 3.1.5 of the ABAQUS Benchmarks Manual, which illustrates the entire process of fitting elastomeric foam constants to a set of test data.
As with incompressible hyperelasticity, ABAQUS checks the Drucker stability of the material for the deformation modes described above. The Drucker stability condition for a compressible material requires that the change in the Kirchhoff stress, ![]() , following from an infinitesimal change in the logarithmic strain,
, following from an infinitesimal change in the logarithmic strain, ![]() , satisfies the inequality
, satisfies the inequality
![]()
![]()
For an isotropic elastic formulation the inequality can be represented in terms of the principal stresses and strains
![]()
Thus, the relation between changes in the stress and changes in the strain can be obtained in the form of the matrix equation
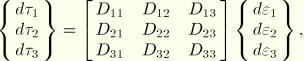
Since ![]() must be positive definite, it is necessary that
must be positive definite, it is necessary that
![]()
![]()
![]()
You should be careful about defining the parameters ![]() ,
, ![]() , and
, and ![]() : especially when
: especially when ![]() , the behavior at higher strains is strongly sensitive to the values of these parameters, and unstable material behavior may result if these values are not defined correctly. When some of the coefficients are strongly negative, instability at higher strain levels is likely to occur. ABAQUS performs a check on the stability of the material for nine different forms of loading—uniaxial tension and compression, equibiaxial tension and compression, simple shear, planar tension and compression, and volumetric tension and compression—for
, the behavior at higher strains is strongly sensitive to the values of these parameters, and unstable material behavior may result if these values are not defined correctly. When some of the coefficients are strongly negative, instability at higher strain levels is likely to occur. ABAQUS performs a check on the stability of the material for nine different forms of loading—uniaxial tension and compression, equibiaxial tension and compression, simple shear, planar tension and compression, and volumetric tension and compression—for ![]() (nominal strain range of
(nominal strain range of ![]() ), at intervals
), at intervals ![]() . If an instability is found, ABAQUS issues a warning message and prints the lowest absolute value of
. If an instability is found, ABAQUS issues a warning message and prints the lowest absolute value of ![]() for which the instability is observed. Ideally, no instability occurs. If instabilities are observed at strain levels that are likely to occur in the analysis, it is strongly recommended that you carefully examine and revise the material input data.
for which the instability is observed. Ideally, no instability occurs. If instabilities are observed at strain levels that are likely to occur in the analysis, it is strongly recommended that you carefully examine and revise the material input data.
“Hyperelastic behavior,” Section 10.5.1, contains suggestions for improving the accuracy and stability of elastomeric modeling. “Fitting of elastomeric foam test data,” Section 3.1.5 of the ABAQUS Benchmarks Manual, illustrates the process of fitting elastomeric foam test data.

The hyperfoam model can be used with solid (continuum) elements, finite-strain shells (except S4), and membranes. However, it cannot be used with one-dimensional solid elements (trusses and beams) or with small-strain shells (STRI3, STRI65, S4R5, S8R, S8R5, S9R5).
For continuum elements elastomeric foam hyperelasticity can be used with pure displacement formulation elements or, in ABAQUS/Standard, with the “hybrid” (mixed formulation) elements. Since elastomeric foams are assumed to be very compressible, the use of hybrid elements will generally not yield any advantage over the use of purely displacement-based elements.

The hyperfoam model must always be used with geometrically nonlinear analyses (“General and linear perturbation procedures,” Section 6.1.2).