Products: ABAQUS/Standard ABAQUS/Explicit ABAQUS/CAE
Thermal expansion effects:
can be defined by specifying thermal expansion coefficients so that ABAQUS can compute thermal strains;
can be isotropic, orthotropic, or fully anisotropic;
are defined as total expansion from a reference temperature;
can be specified as a function of temperature and/or field variables; and
in ABAQUS/Standard can be specified directly in user subroutine UEXPAN (if the thermal strains are complicated functions of field variables and state variables).
Thermal expansion is a material property included in a material definition (see “Material data definition,” Section 9.1.2) except when it refers to the expansion of a gasket whose material properties are not defined as part of a material definition. In that case expansion must be used in conjunction with the gasket behavior definition (see “Defining the gasket behavior directly using a gasket behavior model,” Section 18.6.6).
| Input File Usage: | Use the following options to define thermal expansion for most materials: |
*MATERIAL *EXPANSION Use the following options to define thermal expansion for gaskets whose constitutive response is defined directly as gasket behavior: *GASKET BEHAVIOR *EXPANSION |
| ABAQUS/CAE Usage: | Use the following option in conjunction with other material behaviors, including gasket behavior, to include thermal expansion effects: |
Property module: material editor: Mechanical |
ABAQUS requires thermal expansion coefficients, 
, that define the total thermal expansion from a reference temperature, 
, as shown in Figure 12.1.2–1.
is the thermal expansion coefficient;
is the current temperature;
is the initial temperature;
are the current values of the predefined field variables;
are the initial values of the field variables; and
is the reference temperature for the thermal expansion coefficient.
The second term in the above equation represents the strain due to the difference between the initial temperature, , and the reference temperature, . This term is necessary to enforce the assumption that there is no initial thermal strain for cases in which the reference temperature does not equal the initial temperature.
If the coefficient of thermal expansion, , is not a function of temperature or field variables, the value of the reference temperature, , is not needed. If is a function of temperature or field variables, you can define .
| Input File Usage: | *EXPANSION, ZERO= |
| ABAQUS/CAE Usage: | Property module: material editor: Mechanical |
Total thermal expansion coefficients are commonly available in tables of material properties. However, sometimes you are given thermal expansion data in differential form:
: 
is a series of constant values: 
between and 
; 
between and 
; 
between and 
; etc. Then, 
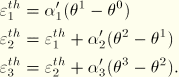
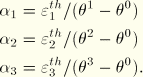
Increments of thermal strain can be specified in ABAQUS/Standard user subroutine UEXPAN as functions of temperature and/or predefined field variables (see “UEXPAN,” Section 25.2.20). User subroutine UEXPAN must be used if the thermal strain increments depend on state variables.
| Input File Usage: | *EXPANSION, USER |
| ABAQUS/CAE Usage: | Property module: material editor: Mechanical |
If the coefficient of thermal expansion, , is a function of temperature or field variables, the initial temperature and initial field variable values, and 
, are given as described in “Initial conditions,” Section 19.2.1.
If an element has been removed and subsequently reactivated in ABAQUS/Standard (“Element and contact pair removal and reactivation,” Section 7.5.1), and in the equation for the thermal strains represent temperature and field variable values as they were at the moment of reactivation.
Isotropic or orthotropic thermal expansion can be defined in ABAQUS. In addition, fully anisotropic thermal expansion can be defined in ABAQUS/Standard.
Orthotropic and anisotropic thermal expansion can be used only with materials where the material directions are defined with local orientations (see “Orientations,” Section 2.2.5).
Orthotropic thermal expansion in ABAQUS/Explicit is allowed only with anisotropic elasticity (including orthotropic elasticity) and anisotropic yield (see “Anisotropic yield/creep,” Section 11.2.6).
Only isotropic thermal expansion is allowed for adiabatic stress analysis and with the hyperelastic and hyperfoam material models.
If the thermal expansion coefficient is defined directly, only one value of is needed at each temperature.
| Input File Usage: | *EXPANSION, TYPE=ISO |
| ABAQUS/CAE Usage: | Property module: material editor: Mechanical |
If user subroutine UEXPAN is used, only one isotropic thermal strain increment (
) must be defined.
| Input File Usage: | *EXPANSION, TYPE=ISO, USER |
| ABAQUS/CAE Usage: | Property module: material editor: Mechanical |
If the thermal expansion coefficients are defined directly, the three expansion coefficients in the principal material directions (
, 
, and 
) should be given as functions of temperature.
| Input File Usage: | *EXPANSION, TYPE=ORTHO |
| ABAQUS/CAE Usage: | Property module: material editor: Mechanical |
If user subroutine UEXPAN is used, the three components of thermal strain increment in the principal material directions (
, 
, and 
) must be defined.
| Input File Usage: | *EXPANSION, TYPE=ORTHO, USER |
| ABAQUS/CAE Usage: | Property module: material editor: Mechanical |
If the thermal expansion coefficients are defined directly, all six components of (, , , 
, 
, 
) must be given as functions of temperature.
| Input File Usage: | *EXPANSION, TYPE=ANISO |
| ABAQUS/CAE Usage: | Property module: material editor: Mechanical |
If user subroutine UEXPAN is used, all six components of the thermal strain increment (, , , 
, 
, 
) must be defined.
| Input File Usage: | *EXPANSION, TYPE=ANISO, USER |
| ABAQUS/CAE Usage: | Property module: material editor: Mechanical |
When a structure is not free to expand, a change in temperature will cause stress. For example, consider a single two-node truss of length 
that is completely restrained at both ends. The cross-sectional area; the Young's modulus, 
; and the thermal expansion coefficient, , are all constant. The stress in this one-dimensional problem can then be calculated from Hooke's Law as 
, where 
is the total strain and 
is the thermal strain, where 
is the temperature change. Since the element is fully restrained, 
. If the temperature at both nodes is the same, we obtain the stress 
.
Constrained thermal expansion can cause significant stress. For typical structural metals, temperature changes of about 150°C (300°F) can cause yield. Therefore, it is often important to define boundary conditions with particular care for problems involving thermal loading to avoid overconstraining the thermal expansion.
Thermal expansion can be combined with any other (mechanical) material (see “Combining material behaviors,” Section 9.1.3) behavior in ABAQUS.
For most materials thermal expansion is defined by a single coefficient or set of orthotropic or anisotropic coefficients or, in ABAQUS/Standard, by defining the incremental thermal strains in user subroutine UEXPAN. For porous media in ABAQUS/Standard, such as soils or rock, thermal expansion can be defined for the solid grains and for the permeating fluid (when using the coupled pore fluid diffusion/stress procedure—see “Coupled pore fluid diffusion and stress analysis,” Section 6.7.1). In such a case the thermal expansion definition should be repeated to define the different thermal expansion effects.
Expansion