
Products: ABAQUS/Standard ABAQUS/CAE

The frequency extraction procedure:
performs eigenvalue extraction to calculate the natural frequencies and the corresponding mode shapes of a system;
will include initial stress and load stiffness effects due to preloads and initial conditions if geometric nonlinearity is accounted for in the base state, so that small vibrations of a preloaded structure can be modeled;
will compute residual modes if requested,
is a linear perturbation procedure; and
can be run in parallel on multiple CPUs by splitting the frequency domain into a number of intervals.

The frequency extraction procedure uses eigenvalue techniques to extract the frequencies of the current system. The eigenvalue problem for the natural frequencies of an undamped finite element model is
![]()
![]()
is the mass matrix (which is symmetric and positive definite);
![]()
is the stiffness matrix (which includes initial stiffness effects if the base state included the effects of nonlinear geometry);
![]()
is the eigenvector (the mode of vibration); and
![]() and
and ![]()
are degrees of freedom.
ABAQUS/Standard offers the Lanczos and the subspace iteration eigenvalue extraction methods—see “Eigenvalue extraction,” Section 2.5.1 of the ABAQUS Theory Manual. The Lanczos method (the default) is generally faster when a large number of eigenmodes is required for a system with many degrees of freedom. The subspace iteration method may be faster when only a few (less than 20) eigenmodes are needed. Subspace iteration and the Lanczos eigensolver can be used for different steps in the same analysis; there is no requirement that the same eigensolver be used for all appropriate steps.
ABAQUS/Standard will solve the eigenfrequency problem only for symmetric matrices. For the subspace iteration procedure you need only specify the number of eigenvalues required; ABAQUS/Standard will choose a suitable number of vectors for the iteration. For the Lanczos method you need to provide the maximum frequency of interest or the number of eigenvalues required; ABAQUS/Standard will determine a suitable block size (although you can override this choice, if needed). If you specify both the maximum frequency of interest and the number of eigenvalues required and the actual number of eigenvalues is underestimated, ABAQUS/Standard will issue a corresponding warning message; the remaining eigenmodes can be found by restarting the frequency extraction. If the parallel Lanczos eigensolver is used (i.e., the number of frequency intervals is set greater than one), you must also provide both the upper and lower frequency boundaries.
In general, the block size for the Lanczos method should be as large as the largest expected multiplicity of eigenvalues (that is, the largest number of modes with the same frequency). A block size larger than 10 is not recommended. If the number of eigenvalues requested is n, the default block size is the minimum of (7, n). The choice of 7 for block size proves to be efficient for problems with rigid body modes. The number of block Lanczos steps within each Lanczos run is usually determined by ABAQUS/Standard but can be changed by you. In general, if a particular type of eigenproblem converges slowly, providing more block Lanczos steps will reduce the analysis cost. On the other hand, if you know that a particular type of problem converges quickly, providing fewer block Lanczos steps will reduce the amount of in-core memory used. The default values are
If the subspace iteration technique is requested, you can also specify the maximum frequency of interest; ABAQUS/Standard will extract eigenvalues until either the requested number of eigenvalues has been extracted or the last frequency extracted exceeds the maximum frequency of interest.
If the Lanczos eigensolver is requested, you can also specify the minimum and/or maximum frequencies of interest; ABAQUS/Standard will extract eigenvalues until either the requested number of eigenvalues has been extracted in the given range or all the frequencies in the given range have been extracted. If the parallel Lanczos eigenvalue extraction method is invoked, you must specify the minimum and maximum frequencies of interest.
| Input File Usage: | Use one of the following options: |
*FREQUENCY, EIGENSOLVER=SUBSPACE *FREQUENCY, EIGENSOLVER=LANCZOS |
| ABAQUS/CAE Usage: | Step module: Step |
If acoustic-structural coupling is present in the model and the Lanczos method is used, ABAQUS/Standard extracts the coupled modes by default. Extraction of the coupled acoustic-structural modes is supported only for the Lanczos eigenvalue extraction method. Coupled acoustic-structural modes cannot be used in subsequent random response or response spectrum analyses. It is possible to ignore coupling when extracting acoustic and structural modes.
| Input File Usage: | *FREQUENCY, ACOUSTIC COUPLING=ON or OFF |
| ABAQUS/CAE Usage: | Step module: Step |
You can specify a positive or negative shifted squared frequency, ![]() . ABAQUS/Standard will extract the eigenfrequencies,
. ABAQUS/Standard will extract the eigenfrequencies, ![]() (in cycles per time), in order of increasing
(in cycles per time), in order of increasing ![]() so that the closest modes to a given frequency will be extracted first. This feature is useful when a particular frequency is of concern or when the natural frequencies of an unrestrained structure are needed. In the latter case a shift from zero (the frequency of the rigid body modes) will avoid singularity problems; a negative frequency shift is normally used. The default is no shift.
so that the closest modes to a given frequency will be extracted first. This feature is useful when a particular frequency is of concern or when the natural frequencies of an unrestrained structure are needed. In the latter case a shift from zero (the frequency of the rigid body modes) will avoid singularity problems; a negative frequency shift is normally used. The default is no shift.
If the Lanczos eigensolver is in use and the user-specified shift is outside the requested frequency range, the shift will be adjusted automatically to a value close to the requested range.
Two types of eigenvector normalization are available for frequency extraction procedures.
By default, the eigenvectors are normalized so that the largest displacement entry in each vector is unity. If the displacements are negligible, as in a torsional mode, the eigenvectors are normalized so that the largest rotation entry in each vector is unity. In a coupled acoustic-structural extraction, if the displacements and rotations in a particular eigenvector are small when compared to the acoustic pressures, the eigenvector is normalized so that the largest acoustic pressure in the eigenvector is unity. The normalization is done before the recovery of dependent degrees of freedom that have been previously eliminated with multi-point constraints or equation constraints. Therefore, it is possible that such degrees of freedom may have values greater than unity.
Alternatively, the eigenvectors can be normalized so that the generalized mass for each vector is unity.
The choice of eigenvector normalization type has no influence on the results of subsequent modal dynamic steps (see “Linear analysis of a rod under dynamic loading,” Section 1.4.9 of the ABAQUS Benchmarks Manual). The normalization type determines only the manner in which the eigenvectors are represented.
In addition to extracting the natural frequencies and mode shapes, ABAQUS/Standard automatically calculates the participation factor, the effective mass, and the composite modal damping for each mode; therefore, these variables are available for use in subsequent linear dynamic analyses.
| Input File Usage: | The first two options are equivalent: |
*FREQUENCY *FREQUENCY, NORMALIZATION=DISPLACEMENT *FREQUENCY, NORMALIZATION=MASS |
| ABAQUS/CAE Usage: | Step module: Step |
The “generalized mass” associated with mode ![]() is
is
![]()
If the eigenvectors are normalized with respect to mass, all the eigenvectors are scaled so that ![]() =1. For coupled acoustic-structural analyses, an acoustic contribution fraction to the generalized mass is computed as well.
=1. For coupled acoustic-structural analyses, an acoustic contribution fraction to the generalized mass is computed as well.
The participation factor for mode ![]() in direction i,
in direction i, ![]() , is a variable that indicates how strongly motion in the global
, is a variable that indicates how strongly motion in the global ![]() -,
-, ![]() -, or
-, or ![]() -direction or rigid body rotation about one of these axes is represented in the eigenvector of that mode. The six possible rigid body motions are indicated by
-direction or rigid body rotation about one of these axes is represented in the eigenvector of that mode. The six possible rigid body motions are indicated by ![]() ,
, ![]() ,
, ![]() ,
, ![]() . The participation factor is defined as
. The participation factor is defined as
![]()
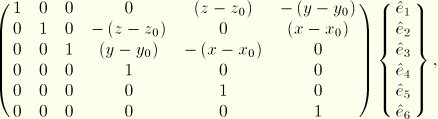
The effective mass for mode ![]() associated with kinematic direction i (
associated with kinematic direction i (![]() ,
, ![]() ,
, ![]() ,
, ![]() ) is defined as
) is defined as
![]()
For coupled acoustic-structural eigenfrequency analysis, an additional acoustic effective mass is computed as outlined in “Coupled acoustic-structural medium analysis,” Section 2.9.1 of the ABAQUS Theory Manual.
You can define composite damping factors for each material (“Material damping,” Section 12.1.1), which are assembled into fractions of critical damping values for each mode, ![]() , according to
, according to
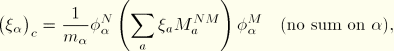
A composite damping value will be calculated for each mode. These values are weighted damping values based on each material's participation in each mode.
| Input File Usage: | *DAMPING, COMPOSITE |
| ABAQUS/CAE Usage: | Property module: Material |
Several analysis types in ABAQUS/Standard are based on the eigenmodes and eigenvalues of the system. For example, in a mode-based steady-state dynamic analysis the mass and stiffness matrices and load vector of the physical system are projected onto a set of eigenmodes resulting in a diagonal system in terms of modal amplitudes (or generalized degrees of freedom). The solution to the physical system is obtained by scaling each eigenmode by its corresponding modal amplitude and superimposing the results (for more information, see “Linear dynamic analysis using modal superposition,” Section 2.5.3 of the ABAQUS Theory Manual).
Due to cost, usually only a small subset of the total possible eigenmodes of the system are extracted, with the subset consisting of eigenmodes corresponding to eigenfrequencies that are close to the excitation frequency. Since excitation frequencies typically fall in the range of the lower modes, it is usually the higher frequency modes that are left out. Depending on the nature of the loading, the accuracy of the modal solution may suffer if too few higher frequency modes are used. Thus, a trade-off exists between accuracy and cost. To minimize the number of modes required for a sufficient degree of accuracy, the set of eigenmodes used in the projection and superposition can be augmented with additional modes known as residual modes. The residual modes help correct for errors introduced by mode truncation. In ABAQUS/Standard a residual mode, ![]() , represents the static response of the structure subjected to a nominal (or unit) load,
, represents the static response of the structure subjected to a nominal (or unit) load, ![]() , corresponding to the actual load that will be used in the mode-based analysis orthogonalized against the extracted eigenmodes,
, corresponding to the actual load that will be used in the mode-based analysis orthogonalized against the extracted eigenmodes,
![]()
This orthogonalization is required to retain the orthogonality properties of the modes (residual and eigen) with respect to mass and stiffness. As a consequence of the mass and stiffness matrices being available, the orthogonalization can be done efficiently during the frequency extraction. Hence, if you wish to include residual modes in subsequent mode-based procedures, you must activate the residual mode calculations in the frequency extraction step. The only requirement is that the static perturbation response of the load that will be applied in the subsequent mode-based analysis (i.e., ![]() ) is available by specifying that load in a static perturbation step immediately preceding the frequency extraction step. If multiple load cases are specified in this static perturbation analysis, one residual mode will be calculated for each load case; otherwise, it is assumed that all loads are part of a single load case, and only one residual mode will be calculated. If the static responses are linearly dependent on each other or the extracted eigenmodes, ABAQUS/Standard automatically will eliminate the redundant responses for the purposes of computing the residual modes.
) is available by specifying that load in a static perturbation step immediately preceding the frequency extraction step. If multiple load cases are specified in this static perturbation analysis, one residual mode will be calculated for each load case; otherwise, it is assumed that all loads are part of a single load case, and only one residual mode will be calculated. If the static responses are linearly dependent on each other or the extracted eigenmodes, ABAQUS/Standard automatically will eliminate the redundant responses for the purposes of computing the residual modes.
When residual modes are requested, the boundary conditions applied in the frequency extraction step must match those applied in the preceding static perturbation step. In addition, in the immediately preceding static perturbation step ABAQUS/Standard requires that (1) if multiple load cases are used, the boundary conditions applied in each load case must be identical, and (2) the boundary condition magnitudes are zero. When generating dynamic substructures (see “Generating a reduced mass matrix for a substructure” in “Defining substructures,” Section 7.2.2), residual modes usually will provide the most benefit if the loading patterns defined in each of the load cases in the preceding static perturbation step match the loading patterns defined under the corresponding substructure load cases in the substructure generation step.
As an outcome of the orthogonalization process, a pseudo-eigenvalue corresponding to each residual mode, ![]() , is computed and given by
, is computed and given by
![]()
You choose to obtain a new set of eigenmodes and residual modes in a new frequency extraction step.
You choose to select a subset of the available eigenmodes and residual modes in the mode-based procedure (selection of modes is described in each of the mode-based analysis type sections).
| Input File Usage: | *FREQUENCY, RESIDUAL MODES |
| ABAQUS/CAE Usage: | Step module: Step |
When frequency-dependent material properties are specified, ABAQUS/Standard offers the option of choosing the frequency at which these properties are evaluated for use in the frequency extraction procedure. This evaluation is necessary because the stiffness cannot be modified during the eigenvalue extraction procedure. If you do not choose the frequency, ABAQUS/Standard evaluates the stiffness associated with frequency-dependent springs and dashpots at zero frequency and does not consider the stiffness contributions from frequency-domain viscoelasticity. If you do specify a frequency, only the real part of the stiffness contributions from frequency-domain viscoelasticity is considered.
Evaluating the properties at a specified frequency is particularly useful in analyses in which the eigenfrequency extraction step is followed by a subspace projection steady-state dynamic step (see “Subspace-based steady-state dynamic analysis,” Section 6.3.9). In these analyses the eigenmodes extracted in the frequency extraction step are used as global basis functions to compute the steady-state dynamic response of a system subjected to harmonic excitation at a number of output frequencies. The accuracy of the results in the subspace projection steady-state dynamic step is improved if you choose to evaluate the material properties at a frequency in the vicinity of the center of the range spanned by the frequencies specified for the steady-state dynamic step.
| Input File Usage: | *FREQUENCY, PROPERTY EVALUATION=frequency |
| ABAQUS/CAE Usage: | Step module: Step |

For problems where a large number of eigenvalues are to be extracted, the Lanczos solver can be run on multiple CPUs using a frequency domain decomposition technique. In this case the frequency domain is split into a specified number of intervals (typically equal to the number of available CPUs), and the extraction is performed on each interval in parallel. You must specify the number of intervals. If you specify a number of intervals that is greater than the number of CPUs requested for the analysis, the number of intervals will be reset to the number of CPUs. If you specify a number of intervals that is less than the number of available CPUs, the additional CPUs will be distributed uniformly among the frequency intervals and used to perform the factorizations (performed for each new shift during the Lanczos algorithm) in parallel.
Setting the number of CPUs to be greater than the number of intervals may be advantageous in cases where disk I/O is the dominant cost and only a single I/O system is available. Each interval performs the I/O intensive backward passes and will compete for the same I/O resources. By assigning multiple CPUs to each of the parallel Lanczos intervals, the factorization process is sped up and the overall I/O cost decreases. To gain a substantial benefit from this mode of operation, the number of degrees of freedom must be sufficiently large so that the parallel sparse solver will benefit from access to multiple CPUs. Since each parallel Lanczos interval works on a different part of the overall spectrum, the memory requirements for running in parallel essentially increase by a factor equal to the number of intervals.
If the number of intervals is greater than one, you must provide both upper and lower frequency ranges.
| Input File Usage: | *FREQUENCY, NUMBER INTERVAL=N |
| ABAQUS/CAE Usage: | Step module: Step |
To operate the Lanczos solver in parallel mode, the frequency domain is split into the number of intervals that you specify and the eigenvalue extraction proceeds independently on each interval. There are several methods available to specify how ABAQUS/Standard will decompose the overall frequency range into the intervals to be run in parallel. The default method is to split the overall frequency range into equally sized intervals.
As an alternative to the default splitting, if you have advanced knowledge of the distribution of eigenvalues, you may wish to specify the exact interval boundaries. In this case you must provide the frequencies that form the internal boundaries. The number of values provided must be exactly equal to the number of frequency intervals minus 1.
| Input File Usage: | *FREQUENCY, NUMBER INTERVAL=N, USER BOUNDARIES |
| ABAQUS/CAE Usage: | Step module: Step |
As an alternative to the direct specification of frequency boundaries, you can choose the frequency intervals such that the interval size changes gradually between the lower and upper frequencies. In this case the internal boundaries are given by:
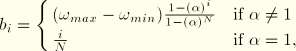
| Input File Usage: | *FREQUENCY, NUMBER INTERVAL=N, BIAS |
| ABAQUS/CAE Usage: | Step module: Step |
Effective use of the parallel Lanczos method requires some knowledge of the expected frequency distribution since the effectiveness of the default splitting method (equally sized intervals) is strongly dependent on the problem. If the number of expected eigenvalues is not provided, the parallel Lanczos method will extract all eigenvalues in all intervals. If the number of eigenvalues is specified for the eigenfrequency extraction, it is interpreted as the total number on all intervals; therefore, if the number of eigenvalues in this range is less than the requested number, some eigenvalues will be discarded upon completion and the method will not be operating optimally.

A continuation/restart capability is available for the Lanczos eigensolver that allows use of eigenmodes from a Lanczos step in a subsequent step where more modes are requested. This is most often useful when, based on examining the modes extracted, you decide that the restart must be performed to obtain more modes. The number of eigenvalues, the frequency range, and the shift point specified for the new Lanczos frequency extraction step are independent of the corresponding requests from the original step. If eigenmodes requested in the new step have already been computed in the original step, the new step will obtain these modes from the original step rather than unnecessarily recomputing these modes. If the parallel Lanczos method is used for extracting additional eigenvalues in the restart step, the modes computed in the original analysis will be used only if the new analysis is expanding the frequency range to the right (i.e., obtaining additional frequencies of greater magnitude). In other cases the frequency extraction will recompute all frequencies before continuing to extract additional eigenvalues. There is no restriction on using the parallel Lanczos technique in the analysis that precedes the restart analysis.
The eigenmodes of a given model may be modified by changes to the step definition since these changes may modify the stiffness and/or the mass matrices. Therefore, if boundary conditions are specified in a Lanczos frequency extraction step, a restart of this step will not use any information from the original step. Whenever possible, specify boundary conditions either as model data (i.e., in the initial step in ABAQUS/CAE) or in a general step that precedes the frequency extraction step.
An original analysis is performed with Step 3 defined as a Lanczos frequency extraction step that computes 100 natural frequencies and the corresponding modes in the range between 100.0 and 200.0 cycles/time.
*RESTART, WRITE … *STEP *FREQUENCY, EIGENSOLVER=LANCZOS 100, 100.0, 200.0 *END STEPIf ABAQUS/Standard discovers that there are more than 100 modes in the range between 100.0 and 200.0 cycles/time, a warning message will be issued to this effect. Restart data are written for this analysis.
You then decide to look for more modes but in the range between 150.0 and 300.0 cycles/time. You perform a restart analysis to find 150 modes using an additional Lanczos frequency extraction step and restarting from Increment 1 of Step 3 of the previous analysis.
*RESTART, READ, STEP=3, INC=1 *STEP *FREQUENCY, EIGENSOLVER=LANCZOS 150, 150.0, 300.0 *END STEPIn this case any modes extracted in the original analysis with frequencies above 150 cycles/time will be reused rather than recomputed.

If the frequency extraction procedure is the first step in an analysis, the initial conditions form the base state for the procedure (except for initial stresses, which cannot be included in the frequency extraction if it is the first step). Otherwise, the base state is the current state of the model at the end of the last general analysis step (“General and linear perturbation procedures,” Section 6.1.2). Initial stress stiffness effects (specified either through defining initial stresses or through loading in a general analysis step) will be included in the eigenvalue extraction only if geometric nonlinearity is considered in a general analysis procedure prior to the frequency extraction procedure.
If initial stresses must be included in the frequency extraction and there is not a general nonlinear step prior to the frequency extraction step, a “dummy” static step—which includes geometric nonlinearity and which maintains the initial stresses with appropriate boundary conditions and loads—must be included before the frequency extraction step.
“Initial conditions,” Section 19.2.1, describes all of the available initial conditions.

Nonzero magnitudes of boundary conditions in a frequency extraction step will be ignored; the degrees of freedom specified will be fixed (“Boundary conditions,” Section 19.3.1).
Boundary conditions defined in a frequency extraction step will not be used in subsequent general analysis steps (unless they are respecified).
If displacements or rotations are to be prescribed in subsequent dynamic modal superposition procedures, boundary conditions must be applied in the frequency extraction step; these degrees of freedom are grouped into “bases.” The bases are then used for prescribing motion in the modal superposition procedure—see “Transient modal dynamic analysis,” Section 6.3.7.
Boundary conditions defined in the frequency extraction step supersede boundary conditions defined in previous steps. Hence, degrees of freedom that were fixed prior to the frequency extraction step will be associated with a specific base if they are redefined with reference to such a base in the frequency extraction step.
By default, all degrees of freedom listed for a boundary condition will be assigned to an unnamed “primary” base. If the same motion will be prescribed at all fixed points, the boundary condition is defined only once; and all prescribed degrees of freedom belong to the primary base.
Unless removed in the frequency extraction step, boundary conditions from the last general analysis step become fixed boundary conditions for the frequency step and belong to the primary base.
If all rigid body motions are not suppressed by the boundary conditions that make up the primary base, you must apply a suitable frequency shift to avoid numerical problems.
| Input File Usage: | *BOUNDARY |
| The *BOUNDARY option without the BASE NAME parameter can appear only once in a frequency extraction step. |
| ABAQUS/CAE Usage: | Load module: Create Boundary Condition |
If the modal superposition procedure will have more than one independent base motion, the driven nodes must be grouped together into “secondary” bases in addition to the primary base. The secondary bases must be named. (See “Base motions in modal-based procedures,” Section 2.5.9 of the ABAQUS Theory Manual.) Secondary bases are used only in modal dynamic and steady-state dynamic (not direct) procedures.
The degrees of freedom associated with secondary bases are not suppressed; instead, a “big” mass is added to each of them. To provide six digits of numerical accuracy, ABAQUS/Standard sets each “big” mass equal to 106 times the total mass of the structure and each “big” rotary inertia equal to 106 times the total moment of inertia of the structure. Hence, an artificial low frequency mode is introduced for every degree of freedom in a secondary base. To keep the requested range of frequencies unchanged, ABAQUS/Standard automatically increases the number of eigenvalues extracted. Consequently, the cost of the eigenvalue extraction step will increase as more degrees of freedom are included in the secondary bases. To reduce the analysis cost, keep the number of degrees of freedom associated with secondary bases to a minimum. This can sometimes be done by reducing several secondary bases that all have the same prescribed motion to a single node by using BEAM type MPCs (“General multi-point constraints,” Section 20.2.2). It is recommended that you use a nonzero shift value for eigenvalue extraction using the Lanczos solver.
The “big” masses are not included in the model statistics, and the total mass of the structure and the printed messages about masses and inertia for the entire model are not affected. However, the presence of the masses will be noticeable in the output tables printed for the eigenvalue extraction step, as well as in the information for the generalized masses and effective masses. See “Double cantilever subjected to multiple base motions,” Section 1.4.12 of the ABAQUS Benchmarks Manual, for an example of the use of the base motion feature.
More than one secondary base can be defined by repeating the boundary condition definition and assigning different base names.
| Input File Usage: | *BOUNDARY, BASE NAME=name |
| ABAQUS/CAE Usage: | Secondary bases are not supported in ABAQUS/CAE. |

Applied loads (“Applying loads: overview,” Section 19.4.1) are ignored during a frequency extraction analysis. If loads were applied in a previous general analysis step and geometric nonlinearity was considered for that prior step, the load stiffness determined at the end of the previous general analysis step is included in the eigenvalue extraction (“General and linear perturbation procedures,” Section 6.1.2).

The density of the material must be defined (“Density,” Section 9.2.1). The following material properties are not active during a frequency extraction: plasticity and other inelastic effects, rate-dependent material properties, thermal properties, mass diffusion properties, electrical properties (although piezoelectric materials are active), and pore fluid flow properties—see “General and linear perturbation procedures,” Section 6.1.2.

Other than generalized axisymmetric elements with twist, any of the stress/displacement elements in ABAQUS/Standard (including those with temperature or pressure degrees of freedom) can be used in a frequency extraction procedure.

The eigenvalues (EIGVAL), eigenfrequencies in cycles/time (EIGFREQ), generalized masses (GM), composite modal damping factors (CD), participation factors for degrees of freedom 1–6 (PF1–PF6), and modal effective masses for degrees of freedom 1–6 (EM1–EM6) are automatically written to the output database as history data. Output variables such as stress, strain, and displacement (which represent mode shapes) are also available for each eigenvalue; these quantities are perturbation values and represent mode shapes, not absolute values.
The eigenvalues and corresponding frequencies (in both radians/time and cycles/time) will also be automatically listed in the printed output file, along with the generalized masses, composite modal damping factors, participation factors, and modal effective masses.
The only energy density available in eigenvalue extraction procedures is the elastic strain energy density, SENER. All of the output variable identifiers are outlined in “ABAQUS/Standard output variable identifiers,” Section 4.2.1.
You can restrict output to the results, data, and output database files by selecting the modes for which output is desired (see “Output to the data and results files,” Section 4.1.2, and “Output to the output database,” Section 4.1.3).
| Input File Usage: | Use one of the following options: |
*EL FILE, MODE, LAST MODE *EL PRINT, MODE, LAST MODE *OUTPUT, MODE LIST |
| ABAQUS/CAE Usage: | Step module: Output |

*HEADING … *BOUNDARY Data lines to specify zero-valued boundary conditions *INITIAL CONDITIONS Data lines to specify initial conditions ** *STEP (,NLGEOM) If NLGEOM is used, initial stress and preload stiffness effects will be included in the frequency extraction step *STATIC … *CLOAD and/or *DLOAD Data lines to specify loads *TEMPERATURE and/or *FIELD Data lines to specify values of predefined fields *BOUNDARY Data lines to specify zero-valued or nonzero boundary conditions *END STEP ** *STEP, PERTURBATION *STATIC … *LOAD CASE, NAME=load case name Keywords and data lines to define loading for this load case *END LOAD CASE … *END STEP** *STEP *FREQUENCY, EIGENSOLVER=LANCZOS, RESIDUAL MODES Data line to control eigenvalue extraction *BOUNDARY *BOUNDARY, BASE NAME=name Data lines to assign degrees of freedom to a secondary base *END STEP