Product: ABAQUS/Standard
The jointed material model is intended to provide a simple, continuum model for materials containing a high density of parallel joint surfaces in different orientations. The spacing of the joints of a particular orientation is assumed to be sufficiently close compared to characteristic dimensions in the domain of the model that the joints can be smeared into a continuum of slip systems. An obvious application is the modeling of geotechnical problems where the medium of interest is composed of significantly faulted rock. In this context, models similar to the one described next have been proposed in the past; see, for example, the model formulated by Zienkiewicz and Pande (1977).
The model implemented in ABAQUS/Standard provides for opening of the joints, or frictional sliding of the joints, in each of these systems (a “system” in this context is a joint orientation in a particular direction at a material calculation point). In addition to the joint systems, the model includes a bulk material failure mechanism. This is based on the Drucker-Prager failure criterion.
We consider a particular joint 
oriented by the normal to the joint surface 
. We define 
as two unit, orthogonal vectors in the joint surface. The local stress components are the pressure stress across the joint
is the stress tensor. We define the shear stress magnitude as 
-direction in the joint surface 
is the strain tensor.A linear strain rate decomposition is assumed, so that
where
is the total strain rate, 
is the elastic strain rate, and 
is the inelastic (plastic) strain rate. Supposing that several systems are active (we designate an active system by 
, where 
indicates the bulk material system and 
is a joint system ), we write When all joints at a point are closed, the elastic behavior of the material is assumed to be isotropic and linear. The material cannot be elastically incompressible (Poisson's ratio must be less than 0.5).
We use a stress-based joint opening criterion whereas joint closing is monitored based on strain. Joint system opens when the estimated pressure stress across the joint (normal to the joint surface) is no longer positive:
is the component of direct elastic strain across the joint and 
is the component of direct elastic strain across the joint calculated in plane stress as
is the Young's modulus of the material, 
is the Poisson's ratio, and 
The shear response of open joints is governed by the shear retention parameter, 
, which represents the fraction of the elastic shear modulus retained when the joints are open (=0 means no shear stiffness associated with open joints, while =1 corresponds to elastic shear stiffness in open joints; any value between these two extremes can be used).
The failure surface for sliding on joint system is defined by
is the friction angle for system , and 
is the cohesion for system (see Figure 4.5.4–1). As long as 
, joint system does not slip. When 
joint system slips. The inelastic (“plastic”) strain on the system is then given by 
is the rate of inelastic shear strain in direction on the joint surface, 
is the magnitude of the inelastic strain rate, 
is the dilation angle for this joint system (choosing 
provides pure shear flow on the joint, while 
causes dilation of the joint as it slips), and 
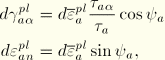
is the inelastic strain normal to the joint surface. In order to add the plastic flow contributions from different systems we write the tensorial plastic strain rate for joint as The sliding of the different joint systems at a point is independent, in the sense that sliding on one system does not change the failure criterion or the dilation angle for any other joint system at the same point. The model provides for up to three joint systems at a point.
In addition to the joint systems, the model includes a bulk material failure mechanism. This is based on the Drucker-Prager failure criterion,
where
is the Mises equivalent deviatoric stress (here 
is the deviatoric stress 
), 
is the equivalent pressure stress, 
is the friction angle for the bulk material, and 
is the cohesion for the bulk material (see Figure 4.5.4–2). If this failure criterion is reached, the bulk inelastic flow is defined by where is the flow potential. Here, 
is the magnitude of the inelastic flow rate (chosen so that 
in uniaxial compression in the 
-direction) and 
is the dilation angle for the bulk material. This bulk failure model is a simplified version of the extended Drucker-Prager model described in “Models for granular or polymer behavior,” Section 4.4.2. As with the joint systems, this bulk failure system is independent of the joint systems, in that bulk inelastic flow does not change the behavior of any joint system.If 
in any system the flow in that system is “nonassociated.” This implies that the material stiffness matrix is not symmetric, so that the unsymmetric matrix solution scheme should be invoked by the user. If the difference between 
and 
is not large, a symmetric approximation to the matrix can provide an acceptable rate of convergence of the equilibrium equations, and hence a lower overall solution cost. For this reason the unsymmetric solver is not automatically invoked for this material behavior. However, it is recommended for all cases where and are very different on any joint system.
