Products: ABAQUS/Standard ABAQUS/Explicit
Truss elements are one-dimensional bars or rods that are assumed to deform by axial stretching only. They are pin jointed at their nodes, and so only translational displacements and the initial position vector at each node are used in the discretization. When the strains are large, the formulation is simplified by assuming that the trusses are made of incompressible material.
There are two truss elements in ABAQUS: a 2-node linear interpolation truss and a 3-node quadratic interpolation truss. The quadratic interpolation version is in the library mainly for compatibility with the quadratic interpolation elements of other types, such as shell element S8R5. The same interpolation functions are used for both the Cartesian displacement components and for the Cartesian components of the initial position vector, so these elements are the simplest form of isoparametric elements.
The elements are one-dimensional: a single material (isoparametric) coordinate, 
, is defined along the element, with 
in the element. In a 2-node element node 1 is at 
and node 2 is at 
. In the 3-node version node 1 is at , node 2 is at 
, and node 3 is at 
.
The interpolation for the 2-node element is
, 
, and 
are the values of a variable at the nodes and 
is the interpolated value of this variable.These are one-dimensional elements, and the only strain considered is that along the axis of the element. The stretch ratio along the axis is
measures length along the truss axis in the current configuration:
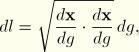
measures length along the axis in the original configuration.For geometrically nonlinear analysis we use a logarithmic strain measure:
The first variation of strain is
Stiffness
The linear truss is a constant strain element and so is integrated exactly. The quadratic truss is integrated numerically using two Gauss points.
Mass and consistent loads
A linear truss has two Gauss points. A quadratic truss has three Gauss points.
The virtual work contribution from the stress in a truss element is
is the current cross-sectional area of the truss, 
is the “true” (Cauchy) stress along the truss, 
is the logarithmic strain, and is the length of the element.Since we assume the truss is incompressible, 
, where 
is the original area and 
the original length of the truss. So,
This is the form in which the internal virtual work contribution is used for truss elements.
“Hybrid” truss elements are also available in ABAQUS/Standard. In those elements the axial force at the integration points is taken as an additional variable, with the compatibility condition introduced to define these variables. The formulation is identical to that used for the hybrid beam elements (“Hybrid beam elements,” Section 3.5.4), without the bending terms.
