
Products: ABAQUS/Standard ABAQUS/Explicit
Membrane elements are sheets in space that can carry membrane force but do not have any bending or transverse shear stiffness, so the only nonzero stress components in the membrane are those components parallel to the middle surface of the membrane: the membrane is in a state of plane stress.
At any time we use a local orthonormal basis system ![]() , where
, where ![]() and
and ![]() are in the surface of the membrane and
are in the surface of the membrane and ![]() is normal to the membrane. The basis system is defined by the standard convention used in ABAQUS for a basis on a surface in space. In this section Greek indices take the range 1, 2, and Latin indices take the range 1, 2, 3. Greek indices are used to refer to components in the first two directions of the local orthonormal basis (in the surface of the membrane).
is normal to the membrane. The basis system is defined by the standard convention used in ABAQUS for a basis on a surface in space. In this section Greek indices take the range 1, 2, and Latin indices take the range 1, 2, 3. Greek indices are used to refer to components in the first two directions of the local orthonormal basis (in the surface of the membrane).

The virtual work contribution from the internal forces in a membrane element is
whereWe assume that only the membrane stress components in the surface of the membrane are nonzero: ![]() . Then Equation 3.4.1–1 simplifies to
. Then Equation 3.4.1–1 simplifies to
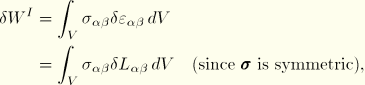
![]()

The consistent Jacobian contribution from the element is
![]()
![]()
![]()
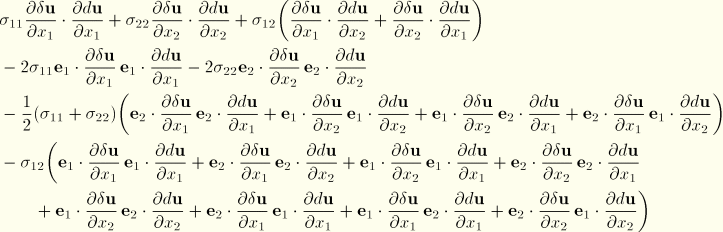

In geometrically nonlinear analyses the cross-section thickness changes as a function of the membrane strain with a user-defined “effective section Poisson's ratio,” ![]() .
.
In plane stress ![]() ; linear elasticity gives
; linear elasticity gives
![]()
![]()
![]()

The deformation gradient is ![]() . Since we take
. Since we take ![]() normal to the current membrane surface and assume no transverse shear of the membrane,
normal to the current membrane surface and assume no transverse shear of the membrane,
![]()
![]()
To calculate the deformation gradient at the end of the increment, first we calculate the two tangent vectors at the end of the increment defined by the derivative of the position with respect to the reference coordinates:
![]()
![]()
To choose the element basis directions ![]() , we do the following. Find any pair of in-plane orthonormal vectors
, we do the following. Find any pair of in-plane orthonormal vectors ![]() (by the standard ABAQUS projection). Then find the angle
(by the standard ABAQUS projection). Then find the angle ![]() such that the element basis vectors
such that the element basis vectors ![]() , defined
, defined
![]()
![]()
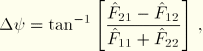
![]()
For elastomers we work directly in terms of ![]() and
and ![]() . For inelastic material models we need measures of incremental strain and average material rotation, which we compute from
. For inelastic material models we need measures of incremental strain and average material rotation, which we compute from ![]() defined by
defined by ![]() , where
, where ![]() is the deformation gradient at the start of the current increment (at increment “
is the deformation gradient at the start of the current increment (at increment “![]() ”):
”):
![]()
![]()
The incremental strain and rotation are then defined from the polar decomposition ![]() , where
, where ![]() is a rotation matrix and
is a rotation matrix and ![]() is a pure stretch:
is a pure stretch:
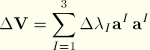
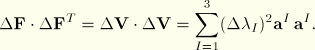
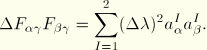
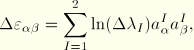
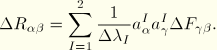
![]()