So far we've seen objects as containers of data with methods to operate on the data. For example, a bank account objects holds a balance; a calorie counter holds grams of fat, protein, and carbohydrates.
But in all of these cases, we knew ahead of time exactly how much data needed to be stored, and we allocated an instance variable to hold each piece of information.
However, we often want to store collections of data such as
So we can't handle this problem by creating an object with a separate instance variable for each piece of data. We need a way to store collections of data that may grow and shrink dynamically over time, and we need to organize the information so that we can access it using efficient algorithms.
The way information is organized in the memory of a computer is called a data structure. Let's explore this idea in terms of a simple example.
Suppose we want to store a list of integers. Let's define an object to hold a single item in the list.
public class ListItem {
public int number;
ListItem(int n) {
number = n;
}
}
This is fine, except that it holds only one number. In a list,
though, we expect that there is some way to scan down the list,
to get to the next item in a list. It turns out that the
instance variables in objects are not limited to primitive data
types. So we can define instance variables that hold
references to other objects. In particular, we can define
an instance variable to refer to the next item in the list.
public class ListItem {
public int number;
public ListItem next; // Reference to the next item in the list
ListItem(int n, ListItem next) {
number = n;
this.next = next;
}
}
How will we mark the end of the list? We will set next =
null.Will this work? Let's see how it looks in memory. For example, suppose we execute the following code:
ListItem a = new ListItem(3, null);
ListItem b = new ListItem(7, a);
ListItem c = new ListItem(4, b);
Each time we execute new, an object is created in
the heap area of the computer's memory. The variables
a, b, and c are on the
stack. Let's draw an object and reference diagram to
show how this looks.
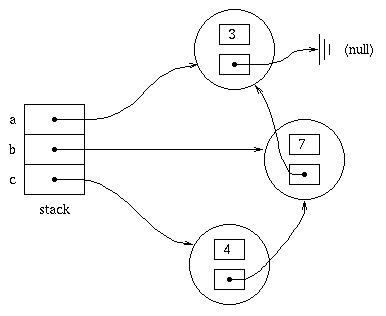
So
a, b, and
c refer to ListItem objectsc refers to, we can
access each number in the list by following the
ListItem references stored in the
next variables of the objects.
toString method to our
ListItem class, so we can print out the contents of
the list.
How will we create a string containing all the numbers in the
list? We can walk down the list recursively. Here the
termination condition is when next is
null, so there are no more items. The recursive
call is next.toString().
public String toString() {
if (next == null)
return (" " + number);
else
return (" " + number + next.toString());
}
(The last line could also be written return (" " + number
+ next);)Using the substitution model, let's trace the execution of
c.toString()
" " + 4 + next.toString()
" " + 4 + " " + 7 + next.toString()
" " + 4 + " " + 7 + " " + 3
" 4 7 3"
Note: next is different for each recursive call,
since it is the reference to the next element of the list
following this.
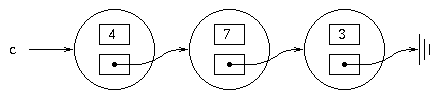
Continuing with our example, suppose we executed c.next =
b.next;
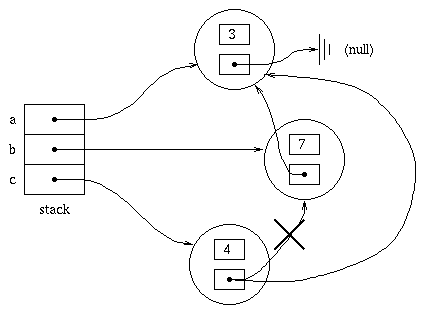
Now, if we evaluate
c.toString()we get
" 4 3"
b.toString()
" 7 3"
a.toString()
" 3"
Notice that the object containing 3 is shared by all
three lists.
In memory, the objects are actually stored at particular
memory addresses, and the references contain the addresses of
the objects they reference. For example, the data structure
above might be stored as follows, with two memory locations
for each object, one holding number and one
holding next.
| Address | Memory |
|---|---|
| 100 | 3 |
| 101 | 0 (null) |
| 102 | 7 |
| 103 | 100 |
| 104 | 4 |
| 105 |
In this case, a would contain a reference to the
address 100, b to address 102, and c
to address 104.
Recursion over Linked Lists
Let's try writing some additional methods for the
ListItem class to get some practice working with
lists.
sum() returns the sum of all the numbers in the
list.
public int sum() {
if (next == null)
return number;
else
return number + next.sum();
}
min() returns the smallest number in the list.
public int min() {
if (next == null)
return number;
else
return Math.min(number, next.min());
}
copy() returns a copy of the list.
public ListItem copy() {
if (next == null)
return new ListItem(number, null);
else
return new ListItem(number, next.copy());
}
Now, how about working with more than one list?
dotProduct(ListItem list) returns the dot product
of this list and the given list. For example,
(2 3 4) · (1 2 3) = 2·1 + 3·2 + 4·3 = 20.
public int dotProduct(ListItem list) {
if (next == null)
return number * list.number;
else
return number * list.number + next.dotProduct(list.next);
}
For example, using the substitution model (and abusing
notation),
(2 3 4).dotProduct((1 2 3))
2 * 1 + (3 4).dotProduct((2 3))
2 * 1 + 3 * 2 + (4).dotProduct((3))
2 * 1 + 3 * 2 + 4 * 3
=> 20
One more: last() returns the last
ListItem in the list.
public ListItem last() {
if (next == null)
return this;
else
return next.last();
}
We have used recursion as a natural way to implement operations
on linked lists. For example, if the ListItem
class contains an integer number and a reference to
the next ListItem, we have processed a
list by performing an operation on the number and combining the
result with a recursive call to process the rest of the list.
For example, to sum all the elements of a list, we can do the
following:
int sumList(ListItem ls) {
if (ls == null)
return 0;
else
return ls.number + sumList(ls.next);
}
Now let's see how to implement a summation procedure using iteration. We can start at the beginning of the list and move down the list with each iteration until we reach the end. As we move down the list, we'll keep track of the sum of all items visited so far.
int sumList(ListItem ls) {
int sum = 0;
while (ls != null) {
sum = sum + ls.number;
ls = ls.next;
}
return sum;
}
Notice that we are assigning to the parameter. Recall that since Java uses call-by-value, this does not affect the calling procedure. However, if we were to implement this iterative procedure as a method on ListItem itself, then we wouldn't have a parameter. In that case, we'd need to declare a local variable, as follows.
pulbic int sumList() {
int sum = 0;
ListItem ls = this;
while (ls != null) {
sum = sum + ls.number;
ls = ls.next;
}
return sum;
}
Let's consider another example, this time modifying the list. We'll scale a list, multiplying each number in the list by a given value. First, recursively,
void scale(ListItem ls, int s) {
if (ls != null) {
ls.number *= s;
scale(ls.next, s);
}
}
Now, compare to the iterative version.
void scale(ListItem ls, int s) {
while (ls != null) {
ls.number *= s;
ls = ls.next;
}
}
Let's consider the same problem, except this time returning a new
scaled list, instead of modifying the given one. First,
recurisvely:
ListItem scale(ListItem ls, int s) {
if (ls == null)
return null;
else
return new ListItem(ls.number * s, scale(ls.next, s));
}
Now iteratively:
ListItem scale(ListItem ls, int s) {
if (ls == null)
return null;
else {
ListItem newList = new ListItem(ls.number * s, null);
ListItem last = newList;
while (ls.next != null) {
ls = ls.next;
last.next = new ListItem(ls.number * s, null);
last = last.next;
}
return newList;
}
}
ListOfInts ADT, and we'll implement it using the
ListItem class we have already defined.As customary in ADT design, let's first consider the different abstract operations we'd like to perform on a list. We'd like operations for determining if the list is empty, and for putting new items at the beginning and the end of the list. Also, we'd like to have a way to move down the list. For this we'll use a "marker" that will keep track of where we are "currently" in the list. Using the marker, we will be able to get the "current" item, replace the value of the current item, insert into the list just before the current item, and delete the current item. It will also be convenient to have a way of checking if the marker is at the end of the list, and to be able to reset the marker to be at the beginning of the list.
| Method | Parameters | Mutates | Returns |
|---|---|---|---|
| constructor | creates an empty list | object reference | |
isEmpty |
true iff the list is empty | ||
prepend |
int n |
puts n at the beginning of the
list |
this (for convenience) |
append |
int n |
puts n at the end of the list |
this (for convenience) |
atEnd |
true iff marker is at the end of the list | ||
reset |
moves marker to the beginning of the list | ||
next |
moves marker to the next item in the list | this (for convenience) |
|
getItem |
returns the "current" item | ||
setItem |
int n |
replaces the "current" item by n |
|
insert |
int n |
puts n in the list just before current item |
|
delete |
|
removes the current item from the list | the item just removed |
toString |
a String representation of the list contents |
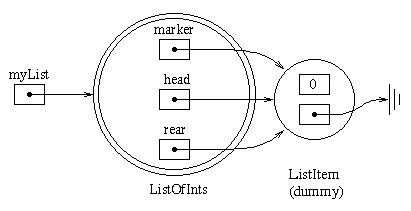
For our internal representation, the ListOfInts object
will contain three instance variables, a marker to keep
track of the "current" list item, the head of the list,
and the rear of the list. All of these will be
ListItem references.
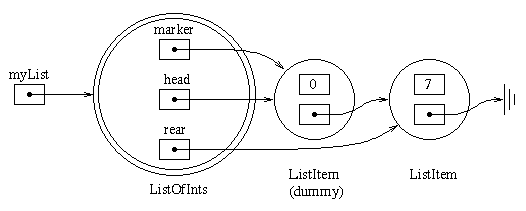
To simplify working with the front of the list, we'll keep a "dummy" ListItem at the head of the data structure. When the list is empty, all three instance variables will refer to the dummy. The dummy is created strictly for our convenience. Since it's not really part of the data being represented, we'll keep it hidden inside the internal representation of the ListOfInts object. We'll put a zero in the dummy ListItem, but it really doesn't matter what value is in the dummy, since we never use its value.
The "current" item will always be the one just after the marker. (In other words, the marker will always refer to the ListItem just before the "current" item.) So, when we reset the marker, we'll position it at the dummy, making the "current" item be the first item in the lest. When the marker refers to the rear ListItem, it will be considered "at the end" of the list, since nothing is after that item.
The following diagram shows the representation for
the list ( 7 3 ). In this example,
marker is referring to the head list item, so the "current" item is 7.

Let's write the code:
import cs101.terminal.*;
public class ListOfInts {
ListItem marker; // the current item is the one after the marker
ListItem head; // always refers to the dummy
ListItem rear; // always refers to the last item in the list
ListOfInts() {
head = rear = marker = new ListItem(0, null); // create dummy
}
public boolean isEmpty() {
return (head.next == null); // alternatively, (head == rear)
}
public ListOfInts prepend(int n) {
head.next = new ListItem(n, head.next);
if (head == rear) // check if this is also the last item
rear = head.next;
return this;
}
public ListOfInts append(int n) {
rear.next = new ListItem(n, null);
rear = rear.next;
return this;
}
public boolean atEnd() {
return (marker.next == null);
}
public void reset() {
marker = head;
}
public ListOfInts next() {
if (!atEnd())
marker = marker.next;
return this;
}
public int getItem() { // gets current item
if (atEnd())
Terminal.println("Error: Tried to get item past end of list!");
else
return marker.next.number;
}
public void setItem(int n) { // replaces value of current item
if (atEnd())
Terminal.println("Error: Tried to set item past end of list!");
else
marker.next.number = n;
}
public void insert(int n) { // inserts n just before the current item, and
// the new item n becomes the current item
if (atEnd()) // appends the item if marker is at the end
append(n);
else
marker.next = new ListItem(n, marker.next);
}
public int delete() { // deletes the current item
if (atEnd()) {
Terminal.println("Error: Tried to delete item past end of list!");
return 0;
}
else {
result = marker.next.number;
if (marker.next == rear)
rear = marker;
marker.next = marker.next.next;
return result;
}
}
public String toString() {
if (isEmpty())
return "( )";
else
return "(" + head.next + " )";
}
}
class ListItem {
public int number;
public ListItem next;
ListItem(int number, ListItem next) {
this.number = number;
this.next = next;
}
public String toString() {
if (this.next == null)
return (" " + number);
else
return (" " + number + this.next);
}
}
ListOfInts myList = new ListOfInts();
myList.append(7);
myList.prepend(4).append(2);
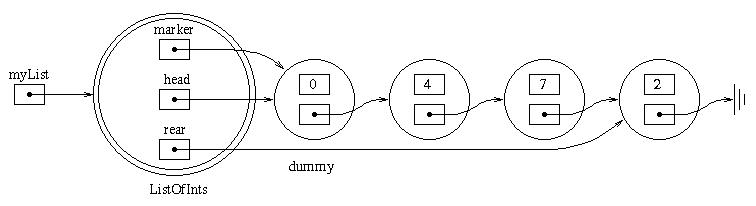
Assuming that memory locations are allocated in order starting at address 100, in memory, this data structure may look like:
| Address | Value |
|---|---|
| 100 | 103 |
| 101 | 103 |
| 102 | |
| 103 | 0 |
| 104 | |
| 105 | 7 |
| 106 | |
| 107 | 4 |
| 108 | 105 |
| 109 | 2 |
| 110 | 0 |
The variable myList would contain a reference to memory
location 100.
Now, if we execute:
myList.next().insert(8);
The new diagram looks like:
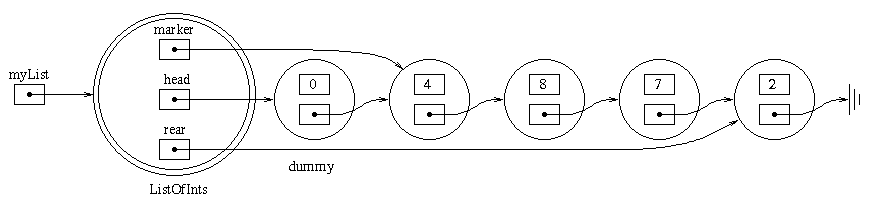
And the memory is updated to contain:
| Address | Value |
|---|---|
| 100 | |
| 101 | 103 |
| 102 | 109 |
| 103 | 0 |
| 104 | 107 |
| 105 | 7 |
| 106 | 109 |
| 107 | 4 |
| 108 | |
| 109 | 2 |
| 110 | 0 |
| 111 | 8 |
| 112 | 105 |
myList.toString() would
return the String "( 4 8 7 2 )".
Recursive Algorithms using the ListOfInts ADT
Let's do some examples of recursion over linked lists, but
instead of using the ListItem objects directly, we'll use the
interface provided by the ListOfInts ADT. For our first example,
let's do a pairwiseMax:
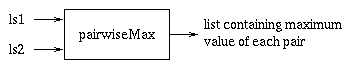
(We'll assume that ls1 and ls2 are the
same length.) For example, if ls1 refers to the
list ( 4 9 3 2 ), and ls2 refers to
the list ( 5 7 1 6 ), then pairwiseMax(ls1,
ls2) would return the list ( 5 9 3 6 ).
We'll also assume that each list has been reset, so that its
marker is at the head of the list.)
ListOfInts pairwiseMax(ListOfInts ls1, ListOfInts ls2) {
if (ls1.atEnd())
return new ListOfInts();
else {
int maxValue = Math.max(ls1.getItem(), ls2.getItem());
return pairwiseMax(ls1.next(), ls2.next()).prepend(maxValue);
}
}
Let's try another example:
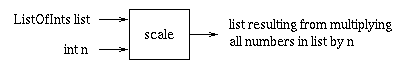
For example, if list referred to the list (
2 3 4 ), then scale(list, 2) would
return the list ( 4 6 8 ).
Again, we'll assume that the list has been reset before
scale is first called.
ListOfInts scale(ListOfInts list, int n) {
if (list.atEnd())
return new ListOfInts();
else {
int scaledValue = n * list.getItem();
return scale(list.next(), n).prepend(scaledValue);
}
}
Why would it be a mistake to replace the body of the
else in the above procedure by the following line?
return scale(list.next(), n).prepend(n * list.getItem()); // ERROR
Note: We assumed that the lists would be reset before the above
procedures were called. To avoid this, one could have the
procedures themselves call reset, but we wouldn't want to reset
the lists on each recursive call. To solve this, we could
call a helper procedure to do the actual recursive computation
after we reset the lists. Alternatively, we could perform the
computations iteratively, as shown below.
Iterative Algorithms using the ListOfInts ADT
Let's write code for the above examples, this time using iteration instead
of recursion. This time, we'll reset the lists as we enter the procedures.
ListOfInts pairwiseMax(ListOfInts ls1, ListOfInts ls2) {
ls1.reset();
ls2.reset();
ListOfInts result = new ListOfInts();
while (!ls1.atEnd()) {
result.append(Math.max(ls1.getItem(), ls2.getItem()));
ls1.next();
ls2.next();
}
return result;
}
ListOfInts scale(ListOfInts list, int n) {
list.reset();
ListOfInts result = new ListOfInts();
while (!list.atEnd()) {
result.append(n * list.getItem());
list.next();
}
return result;
}
Another Algorithm over Lists: Horner's Method
In the polynomial lab, you'll be representing polynomials using
lists of integers. For example, the list ( 2 3 5 )
could be used in a Polynomial object representing
2x2 + 3x + 5.
One method that you'll write for your Polynomial
class is an evaluate method that will find the
value of the polynomial for a given x value. For
example, if f is the above polynomial, then
f.evaluate(3) would return 32, since 2 ·
32 + 3 · 3 + 5 = 18 + 9 + 5 = 32.
This will require you to implement an algorithm that traverses the
list of integers to evaluate the polynomial.
We could do this calculation using brute force, but we would
keep using Math.pow where we don't really have
to. If we factor out x as much as possible, then we
can use fewer multiplicative steps:
5x4 + 7x3 + 2x2 + 3x + 1 = 1 + x(3 + x(2 + x(7 + x(5))))This is known as Horner's method. It lends itself to an easy recursive solution, provided that you reverse the list of coefficients first.
ListItem object
contains a number and a reference to the next item in the list.
Using this basic idea of objects that refer to other objects, we
can build up other kinds of data structures to implement various
abstract data types.
Over the next couple of weeks, we'll look at various abstract
data types and see how to implement them in terms of various
data structures. As we look at these examples, we'll not only
become more comfortable with the concept of a data structure,
but also explore design issues and efficiency concerns.
Example ADT:
A relation is an ADT that captures relationships
(associations) between different objects. For example,
Relation
| Given a: | we might want to know: |
|---|---|
| employee | employer |
| part number | quantity in the warehouse |
| person | mother |
| fruit | its color |
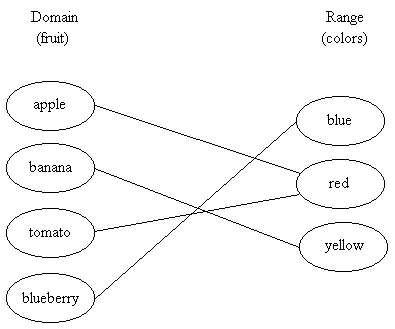
(You did this kind of relation in first grade: "draw a line from the name of the fruit to its color".)
Here, we're going to look at a particular kind of relation called a function -- for each element of the domain, there is exactly one element in the range. (You can think about how to extend this to a relation where, for example, apple could be associated with both red and yellow.)
| Method | Parameters | Mutates (abstractly) | Returns |
|---|---|---|---|
| constructor | (initialization) | reference to an empty relation | |
map |
domain object d and range object
r |
maps d to r |
(void) |
drop |
domain object d |
removes d from relation (if
present) |
the range value associated with the dropped object |
lookup |
domain object d |
range object associated with d, or
null if not present |
If x is a Relation, we expect
that:
x.map(d, r);
lookup(d) => r
x.drop(d);
lookup(d) => null
For example, suppose we have created some Fruit
and Color objects.
Relation x = new Relation();
x.map(apple, red);
x.map(tomato, red);
x.map(apple, green);
x.lookup(apple) => green object
x.drop(apple);
x.lookup(apple) => null
Note: two different objects containing the same
values are still different objects!Association objects that we'll define to
contain a range element and a domain element.
We'll put a dummy Association at the front.d and r? We
could define specific objects types, like Fruit
and Color, and make a relation for those
types. However, then we'd have to create a new kind of
relation if, for example, we wanted a relation between cars
and manufacturers, etc.It turns out that if we declare a reference as
Object foo;
then foo can hold a reference to an object of
any type.
public class Relation {
Association list;
public Relation() {
list = new Association(null, null, null);
}
Association find(Object target) {
// return Assocation _before_ target in list
Association cur = list;
while ((cur.next != null) && (cur.next.domain != target))
cur = cur.next;
return cur;
}
public void map(Object d, Object r) {
Association oneBefore = find(d);
if (oneBefore.next == null)
// didn't find it, so append new item to list end
oneBefore.next = new Association(d, r, null);
else
// did find it, so replace range
oneBefore.next.range = r;
}
public Object drop(Object d) {
Association oneBefore = find(d);
// make sure not at end of list (if it wasn't found, no need to drop)
if (oneBefore.next != null) {
result = oneBefore.next.range;
oneBefore.next = oneBefore.next.next;
return result;
}
else
return null;
}
public Object lookup(Object d) {
Association oneBefore = find(d);
if (oneBefore.next == null)
// didn't find it, return null
return null;
else
return oneBefore.next.range;
}
public String toString() {
String result = "(";
Association cur = list;
while (cur.next != null) {
result = result + cur.next;
cur = cur.next;
}
return result + ")";
}
}
class Association {
Object domain;
Object range;
Association next;
public Association(Object d, Object r, Association next) {
domain = d;
range = r;
this.next = next;
}
public String toString() {
return ( "(" + domain + "," + range + ")" );
}
}
| Method | Parameters | Mutates | Returns |
|---|---|---|---|
| constructor | initializes empty stack | (object reference) | |
push |
Object x |
puts x on top of the stack |
|
pop |
removes Object y from the top if there is
one |
Object y (or null if the
stack is empty) |
|
peek |
reference to the top item (or null) |
||
isEmpty |
true if the stack is empty | ||
toString |
a string containing the contents of the stack |
Expected behavior:
(new Stack()).isEmpty() => true
(new Stack()).push(x).isEmpty() => false
(new Stack()).push(x).peek() => x (stack contains x)
(new Stack()).push(x).pop() => x (stack is empty)
Stack s = new Stack().push(x);
s.peek() => x
s.isEmpty() => false
s.pop() => x
s.isEmpty() => true
s.push(x).push(y).pop() => y
s.pop() => x
Example code to implement the Stack class:
public class ListItem {
public Object item;
public ListItem next;
ListItem(Object item, ListItem next) {
this.item = item;
this.next = next;
}
public String toString() {
if (this.next == null)
return item.toString();
else
return item.toString() + " " + next;
}
}
public class Stack {
ListItem contents;
Stack() {
contents = null;
}
public void push(Object x) {
contents = new ListItem(x,contents);
}
public Object pop() {
if (isEmpty())
return null;
else {
Object topItem = contents.item;
contents = contents.next;
return topItem;
}
}
public Object peek() {
if (isEmpty())
return null;
else
return contents.item;
}
public boolean isEmpty() {
return (contents == null);
}
public String toString() {
if (isEmpty())
return "empty stack";
else
return "stack " + contents;
}
}
Let's design the interface for a queue of objects.
| Method | Parameters | Mutates | Returns |
|---|---|---|---|
| constructor | initializes empty stack | (object reference) | |
enqueue |
Object x |
puts x at the back of the queue |
|
dequeue |
removes the first item from the queue, if there is one | old first item or null |
|
peek |
reference to the front item (or null) |
||
isEmpty |
true if the queue is empty | ||
toString |
a string containing the contents of the queue |
public class Queue {
ListItem front;
ListItem back;
Queue() {
front = back = null;
}
public void enqueue(Object x) {
if (isEmpty())
front = back = new ListItem(x,null);
else {
back.next = new ListItem(x,null);
back = back.next;
}
}
public Object dequeue() {
if (isEmpty())
return null;
else {
Object first = front.item;
front = front.next;
if (front == null)
back = null;
return first;
}
}
public Object peek() {
if (isEmpty())
return null;
else
return front.item;
}
public boolean isEmpty() {
return (front == null);
}
public String toString() {
if (isEmpty())
return "empty queue";
else
return "queue (front to back): " + front;
}
}
Let's consider a circular list of numbers:
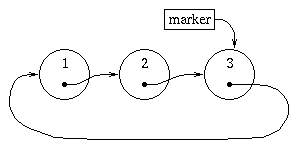
Since the head and the rear of a circular lists depends on your point of view, we'll only keep track of the current position in the list using a marker. At any time, the item referenced by the marker will be called the "rear" of the list, and the next item after the rear will be called the "head" of the list. Now, what kind of interface might we want for this data structure?
| Method | Parameters | Mutates | Returns |
|---|---|---|---|
| constructor | initializes an empty circular list | (reference) | |
insert |
Object x |
puts x just after rear |
|
delete |
removes head of list | object that was in head | |
head |
object in head | ||
move |
moves marker to the next item | ||
isEmpty |
true iff list is empty | ||
toString |
string of contents, front to rear |
public class CircularList {
ListItem marker;
CircularList() {
marker = null;
}
public void insert(Object x) {
if (isEmpty()) {
marker = new ListItem(x,null);
marker.next = marker;
}
else
marker.next = new ListItem(x, marker.next);
}
public Object delete() {
if (isEmpty())
return null;
else {
Object temp = marker.next.item;
if (marker.next == marker)
marker = null;
else
marker.next = marker.next.next;
return temp;
}
}
public Object head() {
if (isEmpty())
return null;
else
return marker.next.item;
}
public void move() {
if (marker != null)
marker = marker.next;
}
public boolean isEmpty() {
return (marker == null);
}
public String toString() {
String result;
if (isEmpty())
result = "empty list";
else {
ListItem head = marker.next;
marker.next = null; // break the cycle
result = head.toString();
marker.next = head; // put the cycle back
}
return result;
}
}
We can now reimplement Stack and
Queue in terms of the circular list ADT:
public class Stack {
CircularList contents;
Stack() {
contents = new CircularList();
}
public void push(Object x) {
contents.insert(x);
}
public Object pop() {
if (isEmpty())
return null;
else {
Object topItem = contents.head();
contents.delete();
return topItem;
}
}
public Object peek() {
if (isEmpty())
return null;
else
return contents.head();
}
public boolean isEmpty() {
return (contents.isEmpty());
}
public String toString() {
if (isEmpty())
return "empty stack";
else
return "stack " + contents;
}
}
public class Queue {
CircularList contents;
Queue() {
contents = new CircularList();
}
public void enqueue(Object x) {
contents.insert(x);
contents.move();
}
public Object dequeue() {
if (isEmpty())
return null;
else {
Object firstItem = contents.head();
contents.delete();
return firstItem;
}
}
public Object peek() {
if (isEmpty())
return null;
else
return contents.head();
}
public boolean isEmpty() {
return (contents.isEmpty());
}
public String toString() {
if (isEmpty())
return "empty queue";
else
return "queue " + contents;
}
}