Nearly all algorithms involve repetition of some sort. Often, the number of repetitions is not known at the time of writing the program, but depends instead on the input values or the size of the input.
So far, we've handled repetition through recursion. We've
directly handled part of the work and made a recursive call to
handle the rest. Examples include not only numerical
algorithms, like factorial, but also algorithms for
traversing data structures. We would, for example, do something
with the first item of the list and then combine it with the
result of a recursive call on the rest of the list.
Although recursion is often the most natural way to think about algorithms that involve repetition, there is another approach, known as iteration (or, more commonly, loops).
To support iteration, Java provides a construct called the
while loop.
while ( boolean expression ) {
loop body
}
true, the
loop body is executed, and execution continues at the top of
the loop, where the test is evaluated again. The loop
terminates when the test fails (evaluates to
false).Usually, some initialization takes place before entering the loop. Let's go back to some algorithms we implemented using recursion and see how they could be implemented using loops.
Recall:
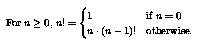
int fact(int n) {
if (n == 0)
return 1;
else
return (n * fact(n - 1));
}
Using a loop, we can write:
int fact(int n) {
int k = 0;
int product = 1; // initialization
while (k < n) { // test
k = k + 1;
product = product * k; // loop body
}
return product;
}
Although people don't use flowcharts much in CS anymore, let's think about the execution of this example using one.
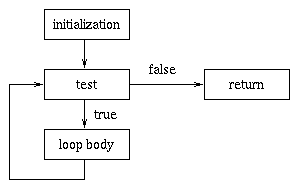
The loop terminates when the test fails, and execution proceeds
immediately to the statement following the loop. So, in this
case, when k=n, the loop terminates, and
execution continues at the return statement.
Let's consider the variable values at each step of the
iteration, finding fact(4).
n | k |
product |
|---|---|---|
| 4 | 0 | 1 |
| 4 | 1 | 1 |
| 4 | 2 | 2 |
| 4 | 3 | 6 |
| 4 | 4 | 24 |
Notice that when we start the loop, and at each iteration, product=k! . This kind of expression, that is always true of the loop variables, is known as a loop invariant.
Using the loop invariant together with the termination condition, we can determine if the return value is correct. In this example, the loop terminates when k=n. So, if k=n on termination, and product=k! is the loop invariant, then substituting, we know that product=n! on termination.
Let's do another example, but this time we'll write the loop invariant before writing the loop, so we can use it to guide us in writing a correct program.
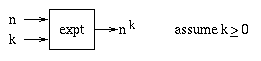
int expt(int n, int k) {
if (k == 0)
return 1;
else
return (n * expt(n, k-1));
}
Now let's write an iterative solution:
int expt(int n, int k) {
// loop invariant: n_to_the_i = ni
int i = 0;
int n_to_the_i = 1;
while (i < k) {
i++;
n_to_the_i *= n;
}
// on termination, i=k, so by the
// loop invariant, n_to_the_i = nk
return n_to_the_i;
}
Of course, we need to check that:
Recall:
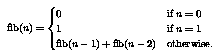
int fib(int n) { // assume n > 0
int k = 1;
int fibk = 1;
int fibk_1 = 0;
// loop invariants: fibk = fibonacci(k)
// fibk_1 = fibonacci(k-1)
while (k < n) {
k++;
int fibk_2 = fibk_1;
fibk_1 = fibk;
fibk = fibk_1 + fibk_2;
}
// on termination, k=n, so by the
// loop invariant, fibk = fibonacci(n)
return fibk;
}
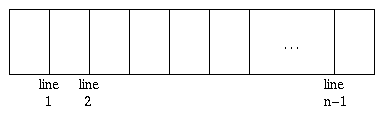
void dividedRectangle(int x, int y, int width, int height, int n,
CS101Canvas screen) {
screen.add(new Rect(x, y, width, height));
int i = 1;
double sizeOfSlice = ((double) width) / n;
double iPosition = x + sizeOfSlice; // position of line 1
while (i < n) {
screen.add(new Line(iPosition, y, iPosition, y + height));
i++;
iPosition += sizeOfSlice;
}
}
Another way to accomplish this, without the counter
i:
void dividedRectangle(int x, int y, int width, int height, int n,
CS101Canvas screen) {
screen.add(new Rect(x, y, width, height));
double position = x;
double sizeOfSlice = ((double) width) / n;
while (position < x + width) {
screen.add(new Line(position, y, position, y + height));
position += sizeOfSlice;
}
}
designRoom procedure in Lab 3, so the couch
potato can rearrange the room by clicking on new positions for
the TV. Now we have to decide When the loop should
terminate. Let's say when the user clicks outside the room.
(Assume that screen, room, and
myTV are already initialized and that we have a
moveTo method on the TV class that
repositions it at the given center position.)
Position p = screen.click(); // get the first position
while (room.inside(p)) {
myTV.moveTo(p);
p = screen.click(); // (What would happen if we omitted this line?)
}
void squares(int x, int y, int size, CS101Canvas screen) {
if (size > 0) {
screen.add(new Rect(x, y, size, size));
squares(x + 5, y + 5, size - 10);
}
}
So, for example, squares(0, 0, 35) would produce
the call sequence
squares(0, 0, 35)
squares(5, 5, 25)
squares(10, 10, 15)
squares(15, 15, 5)
squares(20, 20, -5)
and draw:

void squares(int x, int y, int size, CS101Canvas screen) {
while (size > 0) {
screen.add(new Rect(x, y, size, size));
x += 5;
y += 5;
size -= 10;
}
}