Difference between revisions of "N-Queens/Sudoku Assignment"
(Improved wording and updated changes) |
|||
| (235 intermediate revisions by 3 users not shown) | |||
| Line 1: | Line 1: | ||
| − | = | + | =Motivation= |
| + | Not everything in the world should be divided and conquered. Backtracking is a powerful technique which can be readily parallelized. We will gain experience with backtracking by solving the N-Queens problem and Sudoku in parallel. | ||
| − | + | N-Queens in particular can be used to explain the call stack as the chessboard *IS* the call stack. | |
| − | + | In this assignment, you will implement solutions to both the N-Queens and Sudoku problems. | |
| − | + | =N-Queens= | |
| − | + | [[File:SolvedNQueens8.PNG|250px|thumb|Example solution of N-Queens when n equals 8]] | |
| − | + | ==Background== | |
| + | The n-queens problem is a fundamental coding puzzle which asks: how can N queens be placed on an NxN chessboard so that they cannot attack each other? In chess, a [https://en.wikipedia.org/wiki/Queen_(chess)#Placement_and_movement queen can attack horizontally, vertically, and diagonally] across the board. Thus, to solve the n-queens problem, we must effectively figure out how to place the queens in such a way that no two of them occupy the same row, column, or diagonal. We will be building a method that finds the total number of solutions for n-queens for any given n. | ||
| − | == | + | ==Roadmap to Victory== |
| + | # (Warm Up) SequentialNQueens | ||
| + | # DefaultImmutableQueenLocations | ||
| + | # FirstAvailableRowSearchAlgorithm | ||
| + | # ParallelNQueens | ||
| − | + | ==The Core Questions== | |
| + | *What are the tasks? | ||
| + | *What is the data? | ||
| + | *Is the data mutable? | ||
| + | *If so, how is it shared? | ||
| − | + | ==Code To Implement== | |
| + | ===Sequential Warm Up=== | ||
| + | <nowiki> public static int countSolutions(int boardSize) { | ||
| + | MutableInt count = new MutableInt(); | ||
| + | int[] board = new int[boardSize]; | ||
| + | Arrays.fill(board, EMPTY); | ||
| + | search(count, board, 0); | ||
| + | return count.intValue(); | ||
| + | }</nowiki> | ||
| − | + | {{CodeToImplement|SequentialNQueens|search|nqueens.warmup}} | |
| − | *As <code> | + | |
| + | {{Sequential|private static void search(MutableInt count, int[] board, int row)}} | ||
| + | |||
| + | ===Parallel Studio=== | ||
| + | ====Board State: [https://www.cse.wustl.edu/~cosgroved/courses/cse231/s20/apidocs/nqueens/lab/DefaultImmutableQueenLocations.html DefaultImmutableQueenLocations]==== | ||
| + | {{CodeToImplement|DefaultQueenLocations|createNext<br>getBoardSize<br>getColumnOfQueenInRow<br>getCandidateColumnsInRow|nqueens.lab}} | ||
| + | |||
| + | =====[https://www.cse.wustl.edu/~cosgroved/courses/cse231/current/apidocs/nqueens/core/ImmutableQueenLocations.html#createNext(int,int) createNext(row,col)]===== | ||
| + | {{Sequential|public DefaultQueenLocations createNext(int row, int col)}} | ||
| + | |||
| + | There are two constructors for this class. [https://www.cse.wustl.edu/~cosgroved/courses/cse231/current/apidocs/nqueens/lab/DefaultImmutableQueenLocations.html#DefaultImmutableQueenLocations-int- A public one which creates a fresh new board state with no queens yet placed.] and a private one which creates a new board with the state of a given board which is further constrained by a new queen in the next row. You need to create a new instance using one of these two constructors. Which one is it? | ||
| + | |||
| + | Consider this example program which creates a valid 4-queens solution: | ||
| + | |||
| + | <pre> int boardSize = 4; | ||
| + | QueenLocations board0 = new DefaultQueenLocations(boardSize); | ||
| + | QueenLocations board1 = board0.createNext(0, 1); | ||
| + | QueenLocations board2 = board1.createNext(1, 3); | ||
| + | QueenLocations board3 = board2.createNext(2, 0); | ||
| + | QueenLocations board4 = board3.createNext(3, 2); | ||
| + | System.out.println(board4);</pre> | ||
| + | |||
| + | |||
| + | Which board is used to create the next board? | ||
| + | |||
| + | =====[https://www.cse.wustl.edu/~cosgroved/courses/cse231/current/apidocs/nqueens/core/ImmutableQueenLocations.html#getBoardSize() getBoardSize()]===== | ||
| + | {{Sequential|public int getBoardSize()}} | ||
| + | |||
| + | Note that we will refer to the standard 8x8 chessboard's size as 8 and not 64. | ||
| + | |||
| + | =====[https://www.cse.wustl.edu/~cosgroved/courses/cse231/current/apidocs/nqueens/core/ImmutableQueenLocations.html#getColumnOfQueenInRow(int) getColumnOfQueenInRow(row)]===== | ||
| + | {{Sequential|public Optional<Integer> getColumnOfQueenInRow(int row)}} | ||
| + | |||
| + | For an 8x8 board with queens placed in (row=0, col=1), (row=1, col=6), and (row=2, col=4) | ||
| + | |||
| + | [[File:Queens in rows 012.png|350px]] | ||
| + | |||
| + | * getColumnOfQueenInRow(0) returns [https://docs.oracle.com/javase/8/docs/api/java/util/Optional.html#of-T- Optional.of](1) | ||
| + | * getColumnOfQueenInRow(1) returns [https://docs.oracle.com/javase/8/docs/api/java/util/Optional.html#of-T- Optional.of](6) | ||
| + | * getColumnOfQueenInRow(2) returns [https://docs.oracle.com/javase/8/docs/api/java/util/Optional.html#of-T- Optional.of](4) | ||
| + | * getColumnOfQueenInRow(3) returns [https://docs.oracle.com/javase/8/docs/api/java/util/Optional.html#empty-- Optional.empty()] | ||
| + | * getColumnOfQueenInRow(4) returns [https://docs.oracle.com/javase/8/docs/api/java/util/Optional.html#empty-- Optional.empty()] | ||
| + | * getColumnOfQueenInRow(5) returns [https://docs.oracle.com/javase/8/docs/api/java/util/Optional.html#empty-- Optional.empty()] | ||
| + | * getColumnOfQueenInRow(6) returns [https://docs.oracle.com/javase/8/docs/api/java/util/Optional.html#empty-- Optional.empty()] | ||
| + | * getColumnOfQueenInRow(7) returns [https://docs.oracle.com/javase/8/docs/api/java/util/Optional.html#empty-- Optional.empty()] | ||
| + | |||
| + | =====[https://www.cse.wustl.edu/~cosgroved/courses/cse231/current/apidocs/nqueens/core/ImmutableQueenLocations.html#getCandidateColumnsInRow(int) getCandidateColumnsInRow(row)]===== | ||
| + | {{Sequential|public List<Integer> getCandidateColumnsInRow(int row)}} | ||
| + | |||
| + | For an 8x8 board with a single queen placed in (row=0, col=4) | ||
| + | |||
| + | [[File:Queen_r0_c4.png|350px]] | ||
| + | |||
| + | * getCandidateColumnsInRow(0) returns [] | ||
| + | * getCandidateColumnsInRow(1) returns [0,1,2,6,7] | ||
| + | * getCandidateColumnsInRow(2) returns [0,1,3,5,7] | ||
| + | * getCandidateColumnsInRow(3) returns [0,2,3,5,6] | ||
| + | * getCandidateColumnsInRow(4) returns [1,2,3,5,6,7] | ||
| + | * getCandidateColumnsInRow(5) returns [0,1,2,3,5,6,7] | ||
| + | * getCandidateColumnsInRow(6) returns [0,1,2,3,5,6,7] | ||
| + | * getCandidateColumnsInRow(7) returns [0,1,2,3,5,6,7] | ||
| + | |||
| + | The provided [https://www.cse.wustl.edu/~cosgroved/courses/cse231/current/apidocs/nqueens/core/ImmutableQueenLocations.html#isLocationThreatFree(int,int) isLocationThreatFree(row, col)] method should be helpful. | ||
| + | |||
| + | ====Search Order: [https://www.cse.wustl.edu/~cosgroved/courses/cse231/s20/apidocs/nqueens/lab/FirstAvailableRowSearchAlgorithm.html FirstAvailableRowSearchOrder]==== | ||
| + | This class will provide methods that will allow us to implement a clean and efficient parallel solution in the final step. | ||
| + | |||
| + | {{CodeToImplement|FirstAvailableRowSearchOrder|selectedNextUnplacedRow|nqueens.lab}} | ||
| + | |||
| + | {{Sequential|public Optional<Integer> selectedNextUnplacedRow(QueenLocations queenLocations)}} | ||
| + | |||
| + | For an 8x8 board with queens placed at (row=0, col=0), (row=1, col=3), (row=2, col=6), and (row=6, col=7): | ||
| + | |||
| + | [[File:Queen missing in row3.png|350px]] | ||
| + | |||
| + | * selectedNextUnplacedRow(queenLocations) returns [https://docs.oracle.com/javase/8/docs/api/java/util/Optional.html#of-T- Optional.of](3) | ||
| + | |||
| + | <hr> | ||
| + | |||
| + | For a board with no unplaced rows, for example, a solution: | ||
| + | |||
| + | [[File:8queens solution0.png|350px]] | ||
| + | |||
| + | * selectedNextUnplacedRow(queenLocations) returns [https://docs.oracle.com/javase/8/docs/api/java/util/Optional.html#empty-- Optional.empty()] | ||
| + | |||
| + | <hr> | ||
| + | {{Warning|Do NOT skip empty rows simply because they have no candidate columns}} | ||
| + | |||
| + | In cases where a row does not have a queen placed in it, but has no valid candidate columns, for example a 3x3 board with a queen placed at (row=0, col=1): | ||
| + | |||
| + | [[File:Queen 3x3 eliminates next row.png|200px]] | ||
| + | |||
| + | It is critical that | ||
| + | |||
| + | * selectedNextUnplacedRow(queenLocations) returns [https://docs.oracle.com/javase/8/docs/api/java/util/Optional.html#of-T- Optional.of](1) | ||
| + | |||
| + | When searching for solutions we do not want to avoid dead rows. If anything, we want to move them to the front of the line, so that search can cease the current fruitless path. | ||
| + | |||
| + | ====[https://www.cse.wustl.edu/~cosgroved/courses/cse231/s20/apidocs/nqueens/lab/ParallelNQueens.html ParallelNQueens]==== | ||
| + | Searching for solutions like n-queens can be done in parallel without the need to finish at each level. As such, <code>forasync</code> is preferable to <code>forall</code>. However: | ||
| + | |||
| + | {{Warning|Ensure that you complete all of your tasks by enclosing them a single <code>finish</code>.}} | ||
| + | |||
| + | {{CodeToImplement|ParallelNQueens|searchForSolutions<br>countSolutions|nqueens.lab}} | ||
| + | |||
| + | {{Parallel|public static int countSolutions(QueenLocations queenLocations, RowSearchOrder rowSearchOrder)}} | ||
| + | |||
| + | {{Warning|FinishAccumulators must be registered with their finish statement}} | ||
| + | |||
| + | Instead of using a MutableInt in order to count the number of solutions we have found, we want to use a Finish Accumulator. | ||
| + | |||
| + | Creating a new instance of FinishAccumulator is done via on of the many static methods on the V5 class (the same class we get async and finish from). | ||
| + | |||
| + | Refer to the [[Syntax_of_231#Finish_Accumulators|syntax page]] in order to see the syntax for properly setting up the accumulator. | ||
| + | |||
| + | {{Parallel|private static void searchForSolutions(FinishAccumulator<Integer> accumulator, QueenLocations queenLocations, RowSearchOrder rowSearchOrder)}} | ||
| + | |||
| + | <!-- | ||
| + | ==Tips== | ||
| + | *As <code>QueenLocations</code> is immutable, you will need to create a new instance of the object whenever you move on from one row to the next. This is where <code>createNext</code> comes in, along with the private constructor of this class. | ||
*The <code>isNextRowThreatFree</code> method can easily be completed with a method in <code>AbstractQueenLocations</code>. Refer to that for help. | *The <code>isNextRowThreatFree</code> method can easily be completed with a method in <code>AbstractQueenLocations</code>. Refer to that for help. | ||
*The sequential solution uses <code>MutableQueenLocations</code> while the parallel solution uses your implementation of <code>ImmutableQueenLocations</code>. Be careful to use the correct <code>QueenLocations</code> implementation. | *The sequential solution uses <code>MutableQueenLocations</code> while the parallel solution uses your implementation of <code>ImmutableQueenLocations</code>. Be careful to use the correct <code>QueenLocations</code> implementation. | ||
*As the name suggests, <code>placeQueenInRow</code> will go through the columns of the given row to check if a queen can fit in that location. If it can, it will set that value in <code>MutableQueenLocations</code>. If the examined row is that last row of the board, you have found one valid solution to the n-queens problem. Update the correct parameter accordingly. Otherwise, recurse and keep going until you reach the last row. | *As the name suggests, <code>placeQueenInRow</code> will go through the columns of the given row to check if a queen can fit in that location. If it can, it will set that value in <code>MutableQueenLocations</code>. If the examined row is that last row of the board, you have found one valid solution to the n-queens problem. Update the correct parameter accordingly. Otherwise, recurse and keep going until you reach the last row. | ||
*For the parallel implementation of <code>placeQueenInRow</code>, we are using the "one-finish" pattern. Do not call <code>finish</code> in the recursive method. | *For the parallel implementation of <code>placeQueenInRow</code>, we are using the "one-finish" pattern. Do not call <code>finish</code> in the recursive method. | ||
| − | *The | + | *Go check out the [[Syntax_of_231#Finish_Accumulators|syntax page]] if you have questions on how to set up the Finish Accumulator |
| − | * | + | --> |
| + | |||
| + | =Sudoku= | ||
| + | ==Background== | ||
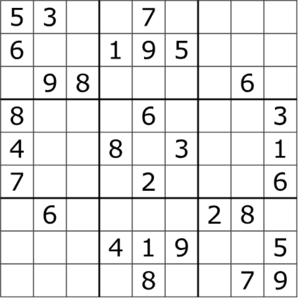
| + | [[File:BasicSudoku.PNG|thumb]] | ||
| + | We will be using a similar algorithm to solve a Sudoku puzzle. For those not familiar, a Sudoku puzzle is composed of a 9-by-9 grid of squares. This grid is also divided into 9 large boxes, each of which is a 3-by-3 of the smaller squares. In a completed puzzle, each of the smaller squares contains a single number from 1 to 9 (inclusive). However, if a square contains a given number, that same number cannot be anywhere else in the same row, column, or box. Thus, for Sudoku, we are given an incomplete board and must fill in the remaining squares while meeting these requirements. | ||
| + | |||
| + | Sudoku is another problem well solved by backtracking. Check the understanding you gained of backtracking with N-Queens by challenging yourself to solve Sudoku's solver without assistance. The game of Sudoku is bit more complex though than N-Queens, and there are more strategies we can do than just backtracking in order to speed up our solution. To make this assignment more compelling, you will implement alternate search orderings and constraint propagation. | ||
| + | |||
| + | Read [http://norvig.com/sudoku.html Peter Norvig's Essay] before you begin coding. It will cover everything related to the Sudoku problem itself and how one can design a solution for it. | ||
| + | |||
| + | ==Roadmap to Victory== | ||
| + | <!-- | ||
| + | There isn't one easiest path through the required files. Some classes utilize methods written in other files, so some students may take a the path such that they will only call methods that are provided or have already implemented. For other students, it might be conceptually easier to start with ParallelSudoku and RowMajorSquareSearchAlgorithm, since these classes closest resembles the work you just did in n-queens. Below is one path that we recommend. In this path, you will build the methods before other methods use them. Many find DefaultConstraintPropagator to be the most challenging part, however. In summary, you can work on these classes in whatever order makes the most sense for you personally. | ||
| + | --> | ||
| + | #PeerEliminationOnlySudokuPuzzle | ||
| + | #RowMajorSearchOrder | ||
| + | #FewestOptionsFirstSearchOrder | ||
| + | #ParallelSudoku | ||
| + | #(Optional Challenge) Add Unit and Twins Constraint Propagation to DefaultConstraintPropagator | ||
| + | |||
| + | ==The Core Questions== | ||
| + | *What are the tasks? | ||
| + | *What is the data? | ||
| + | *Is the data mutable? | ||
| + | *If so, how is it shared? | ||
| + | |||
| + | ==Code To Investigate== | ||
| + | ===Square=== | ||
| + | enum [https://www.cse.wustl.edu/~cosgroved/courses/cse231/current/apidocs/sudoku/core/Square.html Square] | ||
| + | :Collection<Square> [https://www.cse.wustl.edu/~cosgroved/courses/cse231/current/apidocs/sudoku/core/Square.html#getPeers() getPeers()] | ||
| + | :[https://www.cse.wustl.edu/~cosgroved/courses/cse231/current/apidocs/sudoku/core/Square.html#valueOf(int,int) valueOf(row, column)] | ||
| + | :all [https://docs.oracle.com/javase/tutorial/java/javaOO/enum.html enums] have a [https://www.cse.wustl.edu/~cosgroved/courses/cse231/current/apidocs/sudoku/core/Square.html#values() values()] method | ||
| + | |||
| + | ===SudokuUtils=== | ||
| + | class [https://www.cse.wustl.edu/~cosgroved/courses/cse231/current/apidocs/sudoku/core/SudokuUtils.html SudokuUtils] | ||
| + | :[https://www.cse.wustl.edu/~cosgroved/courses/cse231/current/apidocs/sudoku/core/SudokuUtils.html#deepCopyOf(java.util.Map) deepCopyOf(Map<Square, SortedSet<Integer>> other)] | ||
| + | :[https://www.cse.wustl.edu/~cosgroved/courses/cse231/current/apidocs/sudoku/core/SudokuUtils.html#allUnits() allUnits()] | ||
| + | :[https://www.cse.wustl.edu/~cosgroved/courses/cse231/current/apidocs/sudoku/core/SudokuUtils.html#getRowUnit(int) getRowUnit(row)] | ||
| + | :[https://www.cse.wustl.edu/~cosgroved/courses/cse231/current/apidocs/sudoku/core/SudokuUtils.html#getColumnUnit(int) getColumnUnit(col)] | ||
| + | :[https://www.cse.wustl.edu/~cosgroved/courses/cse231/current/apidocs/sudoku/core/SudokuUtils.html#getBoxUnit(int,int) getColumnUnit(row,col)] | ||
| + | :[https://www.cse.wustl.edu/~cosgroved/courses/cse231/current/apidocs/sudoku/core/SudokuUtils.html#getUnitsForSquare(sudoku.core.Square) getUnitsForSquare(square)] | ||
| + | |||
| + | ===CandidateSet=== | ||
| + | class [https://www.cse.wustl.edu/~cosgroved/courses/cse231/current/apidocs/candidate/core/CandidateSet.html CandidateSet<E>] implements [https://docs.oracle.com/javase/8/docs/api/java/util/SortedSet.html SortedSet<E>] | ||
| + | :public static CandidateSet [https://www.cse.wustl.edu/~cosgroved/courses/cse231/current/apidocs/candidate/core/CandidateSet.html#createAllCandidates()-- createAllCandidates()] | ||
| + | <!-- | ||
| + | :public static CandidateSet [https://www.cse.wustl.edu/~cosgroved/courses/cse231/current/apidocs/candidate/core/CandidateSet.html#createSingleOption-- createSingleOption(int option)] | ||
| + | --> | ||
| + | |||
| + | ==Code To Implement== | ||
| + | ===PeerEliminationOnlySudokuPuzzle=== | ||
| + | As the name suggests, <code>DefaultImmutableSudokuPuzzle</code> is immutable, and you will need to create a new instance of the object whenever you move on from one square to the next. This is analogous to the work you did for [[#NQueens]]. | ||
| + | |||
| + | {{CodeToImplement|PeerEliminationOnlySudokuPuzzle|constructors<br>createNext<br>getValue<br>getOptions|sudoku.lab}} | ||
| + | |||
| + | ====constructors==== | ||
| + | The constructors for PeerEliminationOnlySudokuPuzzle have been provided: | ||
| + | |||
| + | =====DefaultImmutableSudokuPuzzle(givens)===== | ||
| + | {{Sequential|public PeerEliminationOnlySudokuPuzzle(String givens)}} | ||
| + | |||
| + | This constructor creates a puzzle constrained to an initial set of givens. You can think of the givens as the original values provided by the newspaper or airline magazine or puzzle book or whatever. | ||
| + | |||
| + | =====PeerEliminationOnlySudokuPuzzle(other,square,value)===== | ||
| + | {{Sequential|private PeerEliminationOnlySudokuPuzzle(PeerEliminationOnlySudokuPuzzle other, Square square, int value)}} | ||
| + | |||
| + | This constructor takes a given previous puzzle and a square value to create a new further constrained puzzle. This will be invoked via a public method on PeerEliminationOnlySudokuPuzzle during the search process. | ||
| + | |||
| + | ====createNext(square,value)==== | ||
| + | {{Sequential|public ImmutableSudokuPuzzle createNext(Square square, int value)}} | ||
| + | |||
| + | This method should create a new puzzle instance using one of the constructors. Which one is it? | ||
| + | |||
| + | ====getValue(square)==== | ||
| + | {{Sequential|public Optional<Integer> getValue(Square square)}} | ||
| + | |||
| + | {{Warning|Ignore any documentation which reports this method should return 0 if it is unfilled.}} | ||
| + | |||
| + | Based on the state of the board, return the value of a given square if it is known. Otherwise, return empty. | ||
| + | |||
| + | How do we determine if a value for a given square is "known"? | ||
| + | |||
| + | ====getCandidates(square)==== | ||
| + | {{Sequential|public SortedSet<Integer> getCandidates(Square square)}} | ||
| + | |||
| + | Based on the state of the board, return the candidate values for a given square. | ||
| + | |||
| + | ===Search Order=== | ||
| + | Simply by changing the search order, a great reduction of work can be achieved. | ||
| + | |||
| + | To implement them, ask yourself: | ||
| + | * How do I determine if a square is filled? | ||
| + | * How do I find the unfilled square with the minimum number of candidates? | ||
| + | |||
| + | When you have completed them, ask yourself: | ||
| + | * Which algorithm will perform better and why? | ||
| + | * What properties make a square "filled"? | ||
| + | |||
| + | {{Warning|Do NOT omit squares with 0 candidates.}} | ||
| + | |||
| + | ====RowMajorSearchOrder==== | ||
| + | {{CodeToImplement|RowMajorSearchOrder|selectNextUnfilledSquare|sudoku.lab}} | ||
| + | {{Sequential|Optional<Square> selectNextUnfilledSquare(ImmutableSudokuPuzzle puzzle)}} | ||
| + | |||
| + | {{Warning|<br>Ignore any documentation which reports this method should return null if it is completely filled.<br>This method should return Optional.empty() for a completely filled board.}} | ||
| + | |||
| + | Simply run through the <code>Square.values()</code> which will iterate through squares going down the row (A1, A2, A3, ...). Make sure not to return squares that have already been filled. | ||
| + | |||
| + | ====FewestOptionsFirstSearchOrder==== | ||
| + | {{CodeToImplement|FewestOptionsFirstSearchOrder|selectNextUnfilledSquare|sudoku.lab}} | ||
| + | {{Sequential|Optional<Square> selectNextUnfilledSquare(ImmutableSudokuPuzzle puzzle)}} | ||
| + | |||
| + | {{Warning|<br>Ignore any documentation which reports this method should return null if it is completely filled.<br>This method should return Optional.empty() for a completely filled board.}} | ||
| + | |||
| + | Go through every square by calling <code>Square.values()</code>, find a square that is (1) not already filled, and (2) has the minimal number of possible options among all the squares, and return that square. | ||
| + | |||
| + | ===Solver=== | ||
| + | This part of the assignment is also similar to its n-queens counterpart. Searching for solutions like sudoku can be done in parallel without the need to finish at each level. As such, <code>forasync</code> is preferable to <code>forall</code> and is, in fact, required by the test. | ||
| − | + | {{Warning|Ensure that you complete all of your tasks by enclosing them all in a single <code>finish</code>.}} | |
| − | + | {{Tip|Use the iterable version of forasync}} | |
| − | + | {{CodeToImplement|ParallelSudoku|solve<br>solveKernel|sudoku.lab}} | |
| − | + | {{Parallel|public static ImmutableSudokuPuzzle solve(ImmutableSudokuPuzzle puzzle, SquareSearchAlgorithm squareSearchAlgorithm)}} | |
| − | + | ||
| − | + | {{Parallel|private static void solveKernel(MutableObject<ImmutableSudokuPuzzle> solution, ImmutableSudokuPuzzle puzzle, SquareSearchAlgorithm squareSearchAlgorithm)}} | |
| − | + | ||
| − | + | =Testing Your Solution= | |
| − | + | ==Visualization== | |
| − | + | ===N-Queens=== | |
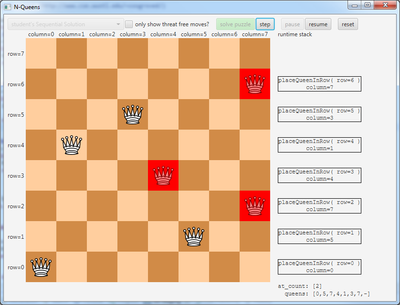
| − | + | {{Viz|NQueensVizApp|nqueens.viz.solution}} | |
| − | + | ||
| + | [[File:NQueensViz.png|400px]] | ||
| + | |||
| + | ===Sudoku=== | ||
| + | ====Propogate==== | ||
| + | {{Viz|SudokuApp|sudoku.viz.solution}} | ||
| + | |||
| + | [[File:SudokuPropagateViz.png|600px]] | ||
| + | |||
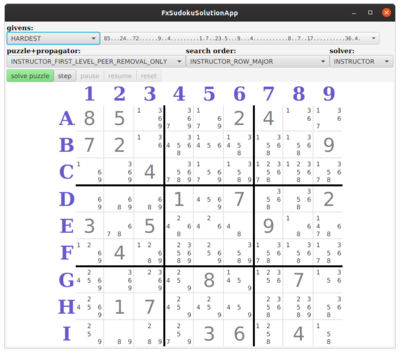
| + | ====Solve==== | ||
| + | {{Viz|FxSudokuSolutionApp|sudoku.viz.solution}} | ||
| + | |||
| + | [[File:SudokuSolutionViz.png|400px]] | ||
| + | |||
| + | ==Correctness== | ||
| + | ===Warm Up=== | ||
| + | {{TestSuite|SequentialNQueensWarmUpTestSuite|nqueens.warmup}} | ||
| + | |||
| + | ===Lab=== | ||
| + | There is a top-level test suite comprised of sub test suites which can be invoked separately when you want to focus on one part of the assignment. | ||
| + | {{TestSuite|BacktrackTestSuite|backtrack.lab}} | ||
| + | |||
| + | ====NQueens==== | ||
| + | {{TestSuite|NQueensTestSuite|nqueens.lab}} | ||
| + | =====ImmutableQueenLocations===== | ||
| + | {{TestSuite|ImmutableQueenLocationsTestSuite|nqueens.lab}} | ||
| + | =====FirstAvailableRowSearchAlgorithm===== | ||
| + | {{TestSuite|FirstAvailableRowSearchTestSuite|nqueens.lab}} | ||
| + | =====ParallelNQueens===== | ||
| + | {{TestSuite|ParallelNQueensSolutionCountTestSuite|nqueens.lab}} | ||
| + | |||
| + | ====Sudoku==== | ||
| + | {{TestSuite|SudokuTestSuite|sudoku.lab}} | ||
| + | =====DefaultConstraintPropagator===== | ||
| + | {{TestSuite|DefaultConstraintPropagatorTestSuite|sudoku.lab}} | ||
| + | =====DefaultImmutableSudokuPuzzle===== | ||
| + | {{TestSuite|DefaultImmutableSudokuPuzzleTestSuite|sudoku.lab}} | ||
| + | =====RowMajorSearchOrder===== | ||
| + | {{TestSuite|RowMajorSearchOrderTestSuite|sudoku.lab}} | ||
| + | =====FewestOptionsFirstOrder===== | ||
| + | {{TestSuite|FewestOptionsFirstOrderTestSuite|sudoku.lab}} | ||
| + | =====ParallelSudokuSolve===== | ||
| + | {{TestSuite|ParallelSudokuSolveTestSuite|sudoku.lab}} | ||
| + | =====Holistic===== | ||
| + | {{TestSuite|HolisticTestSuite|sudoku.lab}} | ||
| + | |||
| + | === Extra Credit Challenge Unit Constraint Propagation === | ||
| + | {{TestSuite|ChallengeSudokuTestSuite|sudoku.challenge}} | ||
=Rubric= | =Rubric= | ||
| Line 48: | Line 350: | ||
Total points: 100 | Total points: 100 | ||
| − | N-Queens subtotal: | + | N-Queens subtotal: 35 |
| − | * Correct | + | * Correct DefaultImmutableQueenLocations (10) |
| − | * Correct | + | * Correct FirstAvailableRowSearchAlgorithm (5) |
| − | * Correct | + | * Correct ParallelNQueens (10) |
| − | + | * Parallel ParallelNQueens (10) | |
| − | Sudoku subtotal: | + | Sudoku subtotal: 65 |
| − | * Correct ImmutableSudokuPuzzle (10) | + | * Correct ImmutableSudokuPuzzle (5) |
| − | * Correct | + | * Correct ContraintPropagator (20) |
| − | * Correct ParallelSudoku ( | + | * Correct RowMajorSearch (10) |
| + | * Correct FewestOptionsFirstSearch (10) | ||
| + | * Correct ParallelSudoku (10) | ||
| + | * Parallel ParallelSudoku (10) | ||
| − | + | Penalties may be assessed for clarity and efficiency. | |
| − | |||
Latest revision as of 20:11, 4 October 2021
Contents
- 1 Motivation
- 2 N-Queens
- 3 Sudoku
- 4 Testing Your Solution
- 5 Rubric
Motivation
Not everything in the world should be divided and conquered. Backtracking is a powerful technique which can be readily parallelized. We will gain experience with backtracking by solving the N-Queens problem and Sudoku in parallel.
N-Queens in particular can be used to explain the call stack as the chessboard *IS* the call stack.
In this assignment, you will implement solutions to both the N-Queens and Sudoku problems.
N-Queens
Background
The n-queens problem is a fundamental coding puzzle which asks: how can N queens be placed on an NxN chessboard so that they cannot attack each other? In chess, a queen can attack horizontally, vertically, and diagonally across the board. Thus, to solve the n-queens problem, we must effectively figure out how to place the queens in such a way that no two of them occupy the same row, column, or diagonal. We will be building a method that finds the total number of solutions for n-queens for any given n.
Roadmap to Victory
- (Warm Up) SequentialNQueens
- DefaultImmutableQueenLocations
- FirstAvailableRowSearchAlgorithm
- ParallelNQueens
The Core Questions
- What are the tasks?
- What is the data?
- Is the data mutable?
- If so, how is it shared?
Code To Implement
Sequential Warm Up
public static int countSolutions(int boardSize) {
MutableInt count = new MutableInt();
int[] board = new int[boardSize];
Arrays.fill(board, EMPTY);
search(count, board, 0);
return count.intValue();
}
| class: | SequentialNQueens.java | |
| methods: | search | |
| package: | nqueens.warmup | |
| source folder: | student/src/main/java |
method: private static void search(MutableInt count, int[] board, int row) ![]() (sequential implementation only)
(sequential implementation only)
Parallel Studio
Board State: DefaultImmutableQueenLocations
| class: | DefaultQueenLocations.java | |
| methods: | createNext getBoardSize getColumnOfQueenInRow getCandidateColumnsInRow |
|
| package: | nqueens.lab | |
| source folder: | student/src/main/java |
createNext(row,col)
method: public DefaultQueenLocations createNext(int row, int col) ![]() (sequential implementation only)
(sequential implementation only)
There are two constructors for this class. A public one which creates a fresh new board state with no queens yet placed. and a private one which creates a new board with the state of a given board which is further constrained by a new queen in the next row. You need to create a new instance using one of these two constructors. Which one is it?
Consider this example program which creates a valid 4-queens solution:
int boardSize = 4; QueenLocations board0 = new DefaultQueenLocations(boardSize); QueenLocations board1 = board0.createNext(0, 1); QueenLocations board2 = board1.createNext(1, 3); QueenLocations board3 = board2.createNext(2, 0); QueenLocations board4 = board3.createNext(3, 2); System.out.println(board4);
Which board is used to create the next board?
getBoardSize()
method: public int getBoardSize() ![]() (sequential implementation only)
(sequential implementation only)
Note that we will refer to the standard 8x8 chessboard's size as 8 and not 64.
getColumnOfQueenInRow(row)
method: public Optional<Integer> getColumnOfQueenInRow(int row) ![]() (sequential implementation only)
(sequential implementation only)
For an 8x8 board with queens placed in (row=0, col=1), (row=1, col=6), and (row=2, col=4)
- getColumnOfQueenInRow(0) returns Optional.of(1)
- getColumnOfQueenInRow(1) returns Optional.of(6)
- getColumnOfQueenInRow(2) returns Optional.of(4)
- getColumnOfQueenInRow(3) returns Optional.empty()
- getColumnOfQueenInRow(4) returns Optional.empty()
- getColumnOfQueenInRow(5) returns Optional.empty()
- getColumnOfQueenInRow(6) returns Optional.empty()
- getColumnOfQueenInRow(7) returns Optional.empty()
getCandidateColumnsInRow(row)
method: public List<Integer> getCandidateColumnsInRow(int row) ![]() (sequential implementation only)
(sequential implementation only)
For an 8x8 board with a single queen placed in (row=0, col=4)
- getCandidateColumnsInRow(0) returns []
- getCandidateColumnsInRow(1) returns [0,1,2,6,7]
- getCandidateColumnsInRow(2) returns [0,1,3,5,7]
- getCandidateColumnsInRow(3) returns [0,2,3,5,6]
- getCandidateColumnsInRow(4) returns [1,2,3,5,6,7]
- getCandidateColumnsInRow(5) returns [0,1,2,3,5,6,7]
- getCandidateColumnsInRow(6) returns [0,1,2,3,5,6,7]
- getCandidateColumnsInRow(7) returns [0,1,2,3,5,6,7]
The provided isLocationThreatFree(row, col) method should be helpful.
Search Order: FirstAvailableRowSearchOrder
This class will provide methods that will allow us to implement a clean and efficient parallel solution in the final step.
| class: | FirstAvailableRowSearchOrder.java | |
| methods: | selectedNextUnplacedRow | |
| package: | nqueens.lab | |
| source folder: | student/src/main/java |
method: public Optional<Integer> selectedNextUnplacedRow(QueenLocations queenLocations) ![]() (sequential implementation only)
(sequential implementation only)
For an 8x8 board with queens placed at (row=0, col=0), (row=1, col=3), (row=2, col=6), and (row=6, col=7):
- selectedNextUnplacedRow(queenLocations) returns Optional.of(3)
For a board with no unplaced rows, for example, a solution:
- selectedNextUnplacedRow(queenLocations) returns Optional.empty()
In cases where a row does not have a queen placed in it, but has no valid candidate columns, for example a 3x3 board with a queen placed at (row=0, col=1):
It is critical that
- selectedNextUnplacedRow(queenLocations) returns Optional.of(1)
When searching for solutions we do not want to avoid dead rows. If anything, we want to move them to the front of the line, so that search can cease the current fruitless path.
ParallelNQueens
Searching for solutions like n-queens can be done in parallel without the need to finish at each level. As such, forasync is preferable to forall. However:
finish. |
| class: | ParallelNQueens.java | |
| methods: | searchForSolutions countSolutions |
|
| package: | nqueens.lab | |
| source folder: | student/src/main/java |
method: public static int countSolutions(QueenLocations queenLocations, RowSearchOrder rowSearchOrder) ![]() (parallel implementation required)
(parallel implementation required)
Instead of using a MutableInt in order to count the number of solutions we have found, we want to use a Finish Accumulator.
Creating a new instance of FinishAccumulator is done via on of the many static methods on the V5 class (the same class we get async and finish from).
Refer to the syntax page in order to see the syntax for properly setting up the accumulator.
method: private static void searchForSolutions(FinishAccumulator<Integer> accumulator, QueenLocations queenLocations, RowSearchOrder rowSearchOrder) ![]() (parallel implementation required)
(parallel implementation required)
Sudoku
Background
We will be using a similar algorithm to solve a Sudoku puzzle. For those not familiar, a Sudoku puzzle is composed of a 9-by-9 grid of squares. This grid is also divided into 9 large boxes, each of which is a 3-by-3 of the smaller squares. In a completed puzzle, each of the smaller squares contains a single number from 1 to 9 (inclusive). However, if a square contains a given number, that same number cannot be anywhere else in the same row, column, or box. Thus, for Sudoku, we are given an incomplete board and must fill in the remaining squares while meeting these requirements.
Sudoku is another problem well solved by backtracking. Check the understanding you gained of backtracking with N-Queens by challenging yourself to solve Sudoku's solver without assistance. The game of Sudoku is bit more complex though than N-Queens, and there are more strategies we can do than just backtracking in order to speed up our solution. To make this assignment more compelling, you will implement alternate search orderings and constraint propagation.
Read Peter Norvig's Essay before you begin coding. It will cover everything related to the Sudoku problem itself and how one can design a solution for it.
Roadmap to Victory
- PeerEliminationOnlySudokuPuzzle
- RowMajorSearchOrder
- FewestOptionsFirstSearchOrder
- ParallelSudoku
- (Optional Challenge) Add Unit and Twins Constraint Propagation to DefaultConstraintPropagator
The Core Questions
- What are the tasks?
- What is the data?
- Is the data mutable?
- If so, how is it shared?
Code To Investigate
Square
enum Square
- Collection<Square> getPeers()
- valueOf(row, column)
- all enums have a values() method
SudokuUtils
class SudokuUtils
- deepCopyOf(Map<Square, SortedSet<Integer>> other)
- allUnits()
- getRowUnit(row)
- getColumnUnit(col)
- getColumnUnit(row,col)
- getUnitsForSquare(square)
CandidateSet
class CandidateSet<E> implements SortedSet<E>
- public static CandidateSet createAllCandidates()
Code To Implement
PeerEliminationOnlySudokuPuzzle
As the name suggests, DefaultImmutableSudokuPuzzle is immutable, and you will need to create a new instance of the object whenever you move on from one square to the next. This is analogous to the work you did for #NQueens.
| class: | PeerEliminationOnlySudokuPuzzle.java | |
| methods: | constructors createNext getValue getOptions |
|
| package: | sudoku.lab | |
| source folder: | student/src/main/java |
constructors
The constructors for PeerEliminationOnlySudokuPuzzle have been provided:
DefaultImmutableSudokuPuzzle(givens)
method: public PeerEliminationOnlySudokuPuzzle(String givens) ![]() (sequential implementation only)
(sequential implementation only)
This constructor creates a puzzle constrained to an initial set of givens. You can think of the givens as the original values provided by the newspaper or airline magazine or puzzle book or whatever.
PeerEliminationOnlySudokuPuzzle(other,square,value)
method: private PeerEliminationOnlySudokuPuzzle(PeerEliminationOnlySudokuPuzzle other, Square square, int value) ![]() (sequential implementation only)
(sequential implementation only)
This constructor takes a given previous puzzle and a square value to create a new further constrained puzzle. This will be invoked via a public method on PeerEliminationOnlySudokuPuzzle during the search process.
createNext(square,value)
method: public ImmutableSudokuPuzzle createNext(Square square, int value) ![]() (sequential implementation only)
(sequential implementation only)
This method should create a new puzzle instance using one of the constructors. Which one is it?
getValue(square)
method: public Optional<Integer> getValue(Square square) ![]() (sequential implementation only)
(sequential implementation only)
Based on the state of the board, return the value of a given square if it is known. Otherwise, return empty.
How do we determine if a value for a given square is "known"?
getCandidates(square)
method: public SortedSet<Integer> getCandidates(Square square) ![]() (sequential implementation only)
(sequential implementation only)
Based on the state of the board, return the candidate values for a given square.
Search Order
Simply by changing the search order, a great reduction of work can be achieved.
To implement them, ask yourself:
- How do I determine if a square is filled?
- How do I find the unfilled square with the minimum number of candidates?
When you have completed them, ask yourself:
- Which algorithm will perform better and why?
- What properties make a square "filled"?
RowMajorSearchOrder
| class: | RowMajorSearchOrder.java | |
| methods: | selectNextUnfilledSquare | |
| package: | sudoku.lab | |
| source folder: | student/src/main/java |
method: Optional<Square> selectNextUnfilledSquare(ImmutableSudokuPuzzle puzzle) ![]() (sequential implementation only)
(sequential implementation only)
Ignore any documentation which reports this method should return null if it is completely filled. This method should return Optional.empty() for a completely filled board. |
Simply run through the Square.values() which will iterate through squares going down the row (A1, A2, A3, ...). Make sure not to return squares that have already been filled.
FewestOptionsFirstSearchOrder
| class: | FewestOptionsFirstSearchOrder.java | |
| methods: | selectNextUnfilledSquare | |
| package: | sudoku.lab | |
| source folder: | student/src/main/java |
method: Optional<Square> selectNextUnfilledSquare(ImmutableSudokuPuzzle puzzle) ![]() (sequential implementation only)
(sequential implementation only)
Ignore any documentation which reports this method should return null if it is completely filled. This method should return Optional.empty() for a completely filled board. |
Go through every square by calling Square.values(), find a square that is (1) not already filled, and (2) has the minimal number of possible options among all the squares, and return that square.
Solver
This part of the assignment is also similar to its n-queens counterpart. Searching for solutions like sudoku can be done in parallel without the need to finish at each level. As such, forasync is preferable to forall and is, in fact, required by the test.
finish. |
| class: | ParallelSudoku.java | |
| methods: | solve solveKernel |
|
| package: | sudoku.lab | |
| source folder: | student/src/main/java |
method: public static ImmutableSudokuPuzzle solve(ImmutableSudokuPuzzle puzzle, SquareSearchAlgorithm squareSearchAlgorithm) ![]() (parallel implementation required)
(parallel implementation required)
method: private static void solveKernel(MutableObject<ImmutableSudokuPuzzle> solution, ImmutableSudokuPuzzle puzzle, SquareSearchAlgorithm squareSearchAlgorithm) ![]() (parallel implementation required)
(parallel implementation required)
Testing Your Solution
Visualization
N-Queens
| class: | NQueensVizApp.java | VIZ |
| package: | nqueens.viz.solution | |
| source folder: | student/src//java |
Sudoku
Propogate
| class: | SudokuApp.java | VIZ |
| package: | sudoku.viz.solution | |
| source folder: | student/src//java |
Solve
| class: | FxSudokuSolutionApp.java | VIZ |
| package: | sudoku.viz.solution | |
| source folder: | student/src//java |
Correctness
Warm Up
| class: | SequentialNQueensWarmUpTestSuite.java | |
| package: | nqueens.warmup | |
| source folder: | testing/src/test/java |
Lab
There is a top-level test suite comprised of sub test suites which can be invoked separately when you want to focus on one part of the assignment.
| class: | BacktrackTestSuite.java | |
| package: | backtrack.lab | |
| source folder: | testing/src/test/java |
NQueens
| class: | NQueensTestSuite.java | |
| package: | nqueens.lab | |
| source folder: | testing/src/test/java |
ImmutableQueenLocations
| class: | ImmutableQueenLocationsTestSuite.java | |
| package: | nqueens.lab | |
| source folder: | testing/src/test/java |
FirstAvailableRowSearchAlgorithm
| class: | FirstAvailableRowSearchTestSuite.java | |
| package: | nqueens.lab | |
| source folder: | testing/src/test/java |
ParallelNQueens
| class: | ParallelNQueensSolutionCountTestSuite.java | |
| package: | nqueens.lab | |
| source folder: | testing/src/test/java |
Sudoku
| class: | SudokuTestSuite.java | |
| package: | sudoku.lab | |
| source folder: | testing/src/test/java |
DefaultConstraintPropagator
| class: | DefaultConstraintPropagatorTestSuite.java | |
| package: | sudoku.lab | |
| source folder: | testing/src/test/java |
DefaultImmutableSudokuPuzzle
| class: | DefaultImmutableSudokuPuzzleTestSuite.java | |
| package: | sudoku.lab | |
| source folder: | testing/src/test/java |
RowMajorSearchOrder
| class: | RowMajorSearchOrderTestSuite.java | |
| package: | sudoku.lab | |
| source folder: | testing/src/test/java |
FewestOptionsFirstOrder
| class: | FewestOptionsFirstOrderTestSuite.java | |
| package: | sudoku.lab | |
| source folder: | testing/src/test/java |
ParallelSudokuSolve
| class: | ParallelSudokuSolveTestSuite.java | |
| package: | sudoku.lab | |
| source folder: | testing/src/test/java |
Holistic
| class: | HolisticTestSuite.java | |
| package: | sudoku.lab | |
| source folder: | testing/src/test/java |
Extra Credit Challenge Unit Constraint Propagation
| class: | ChallengeSudokuTestSuite.java | |
| package: | sudoku.challenge | |
| source folder: | testing/src/test/java |
Rubric
As always, please make sure to cite your work appropriately.
Total points: 100
N-Queens subtotal: 35
- Correct DefaultImmutableQueenLocations (10)
- Correct FirstAvailableRowSearchAlgorithm (5)
- Correct ParallelNQueens (10)
- Parallel ParallelNQueens (10)
Sudoku subtotal: 65
- Correct ImmutableSudokuPuzzle (5)
- Correct ContraintPropagator (20)
- Correct RowMajorSearch (10)
- Correct FewestOptionsFirstSearch (10)
- Correct ParallelSudoku (10)
- Parallel ParallelSudoku (10)
Penalties may be assessed for clarity and efficiency.