
Product: ABAQUS/Aqua
This is a linearized wave theory based on irrotational flow of an inviscid incompressible fluid. The linearization is achieved by assuming the wave height a is small compared to the wavelength ![]() and the still water depth. It is also assumed that the fluid is of uniform depth (that is, the bottom is flat).
and the still water depth. It is also assumed that the fluid is of uniform depth (that is, the bottom is flat).
Since we have irrotational flow, there exists a flow potential, ![]() , obeying
, obeying
Now assume there is a potential energy per unit mass, G, (in this case associated with the gravity field). Then, equilibrium is given by
where![]()
The term ![]() can be neglected compared to the other terms (this can be shown, from the resulting solution, to be consistent with the order of approximation that the wave height is small compared to the wavelength). By choosing the z-coordinate to point vertically upward, the gravity potential is conveniently chosen as
can be neglected compared to the other terms (this can be shown, from the resulting solution, to be consistent with the order of approximation that the wave height is small compared to the wavelength). By choosing the z-coordinate to point vertically upward, the gravity potential is conveniently chosen as
![]()
![]()
![]()
Let ![]() be the elevation of the fluid surface at time t above the mean (undisturbed) fluid surface level,
be the elevation of the fluid surface at time t above the mean (undisturbed) fluid surface level, ![]() . Since the position of the free surface is a part of the solution, there are two boundary conditions that must be applied on
. Since the position of the free surface is a part of the solution, there are two boundary conditions that must be applied on ![]() . The first is a dynamic equilibrium condition at the interface between the fluid and the air. Since the interface is assumed to have no mass, the forces normal to the interface in the fluid and the air must be equal. If the surface tension of the interface is neglected, the pressure in the water and the air must be equal at the interface. Assuming that the pressure due to the motion of the air is negligible (which can be shown to be reasonable), the air pressure can be approximated by its undisturbed value (Whitham, 1974). The dynamic boundary condition then implies
. The first is a dynamic equilibrium condition at the interface between the fluid and the air. Since the interface is assumed to have no mass, the forces normal to the interface in the fluid and the air must be equal. If the surface tension of the interface is neglected, the pressure in the water and the air must be equal at the interface. Assuming that the pressure due to the motion of the air is negligible (which can be shown to be reasonable), the air pressure can be approximated by its undisturbed value (Whitham, 1974). The dynamic boundary condition then implies ![]() , where p is the pressure in the water at the free surface and
, where p is the pressure in the water at the free surface and ![]() is the pressure in the undisturbed air. Since
is the pressure in the undisturbed air. Since ![]() is assumed to be small with respect to the depth of fluid, the boundary condition can be made linear by applying it at
is assumed to be small with respect to the depth of fluid, the boundary condition can be made linear by applying it at ![]() instead of at
instead of at ![]() .
.
With these assumptions Equation 6.2.2–5 provides the boundary term
The second boundary condition on the free surface comes from the kinematics of the free surface. Let the free surface be given by
![]()
Differentiating this expression with respect to time yields
![]()
The problem is now defined by Equation 6.2.2–1, Equation 6.2.2–8, Equation 6.2.2–9, and the requirement that the solution be a plane wave periodic in the horizontal plane, such that
![]()
We solve the problem by assuming that ![]() . Since P and
. Since P and ![]() are independent functions, Equation 6.2.2–1 provides the two equations
are independent functions, Equation 6.2.2–1 provides the two equations
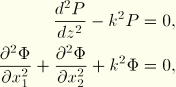
Let ![]() (so that s measures distance in the direction of travel of the wave). The solution to these equations is
(so that s measures distance in the direction of travel of the wave). The solution to these equations is ![]() and
and ![]() hence,
hence,
There is no motion at the bottom of the fluid in the vertical direction, so by Equation 6.2.2–9 we find
![]()
Substituting this into Equation 6.2.2–10 gives
where C is a constant.The dispersion relation can be obtained by substituting Equation 6.2.2–11 into Equation 6.2.2–8 and setting ![]() , giving
, giving
The free surface elevation above the undisturbed fluid surface, ![]() , is given by Equation 6.2.2–6:
, is given by Equation 6.2.2–6:
![]()
This solution provides fluid particle velocities ![]() and accelerations throughout the fluid for this one wave component. The term
and accelerations throughout the fluid for this one wave component. The term ![]() in Equation 6.2.2–4 was neglected because the wave amplitude a is small compared to the wavelength
in Equation 6.2.2–4 was neglected because the wave amplitude a is small compared to the wavelength ![]() . This implies, from Equation 6.2.2–3, that the fluid particle acceleration is approximated as
. This implies, from Equation 6.2.2–3, that the fluid particle acceleration is approximated as ![]() ; that is, the convective part of the acceleration,
; that is, the convective part of the acceleration, ![]() , is neglected.
, is neglected.
Since the theory is linear, any set of waves can be superposed by linear superposition of its components:
![]()
For ![]() :
:
Velocity potential:
![]()
horizontally,
![]()
and vertically,
![]()
horizontally,
![]()
and vertically,
![]()
Fluid particle accelerations:
horizontally,
![]()
and vertically,
![]()
Free surface profile:
![]()
![]()
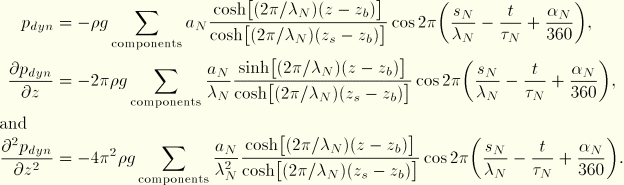
Airy wave theory is a linearized theory; however, the wave amplitude can be large compared with the size of a structure. We, therefore, must make an assumption about the wave kinematics below a crest and above the mean water level. The assumption used here follows modified Airy wave theory as described in Hansen (1988) and Faltinsen (1990). The free surface boundary condition has been made linear in Equation 6.2.2–6. Above the mean or undisturbed surface level ![]() the velocity, acceleration, and dynamic pressure are extrapolated from their values at the mean surface level. Hence, for
the velocity, acceleration, and dynamic pressure are extrapolated from their values at the mean surface level. Hence, for ![]()
![]()
![]()
When a gravity wave is defined, the penetration of the structure into the fluid must be calculated. Although the Airy wave theory assumes that the fluid displacements are small with respect to the wavelength and the fluid depth, they cannot be small with respect to the dimensions of the structure immersed in the fluid. Hence, the instantaneous fluid surface is used to determine if a point on the structure sees loads due to the presence of the fluid.
The Airy wave field is a spatial description of the wave field. The wave field defines velocity, acceleration, and dynamic pressure at spatial locations for all values of time. Hence, the velocity, acceleration, and dynamic pressure are determined by using the current (for geometrically nonlinear analysis) or reference (for geometrically linear analysis) location of the structure at the current time in the appropriate equations. The time used in the wave field equations is the total time for the analysis, which accumulates over all steps in the analysis (static, dynamic, etc.).