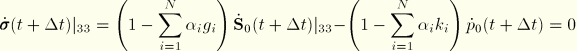Products: ABAQUS/Standard ABAQUS/Explicit

The finite-strain viscoelasticity theory implemented in ABAQUS is a time domain generalization of either the hyperelastic or hyperfoam constitutive models. It is assumed that the instantaneous response of the material follows from the hyperelastic constitutive equations:
![]()
![]()
![]()
![]()
Using integration by parts and a variable transformation, the basic hereditary integral formulation for linear isotropic viscoelasticity can be written in the form
![]()
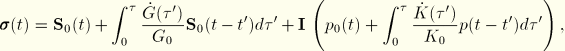
![]()
A suitable generalization to finite strain of the hereditary integral formulation is obtained as follows:
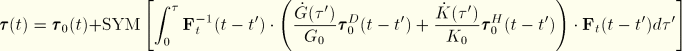
![]()
![]()

As in small-strain viscoelasticity, we represent the relaxation moduli in terms of the Prony series
whereSubstituting Equation 4.8.2–2 and Equation 4.8.2–3 in Equation 4.8.2–1, we obtain
Next, we introduce the internal stresses, associated with each term of the series
These stresses are stored at each material point and are integrated forward in time. We will assume that the solution is known at time t, and we need to construct the solution at time
The internal hydrostatic stresses ![]() at time
at time ![]() follow from
follow from
![]()
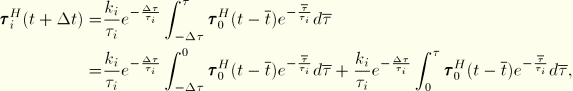
To integrate the first integral in Equation 4.8.2–7, we assume that ![]() varies linearly with the reduced time
varies linearly with the reduced time ![]() over the increment
over the increment
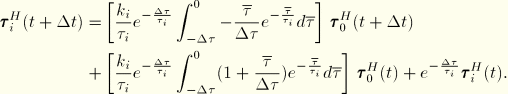
The integrals are readily evaluated, providing the solution at the end of the increment
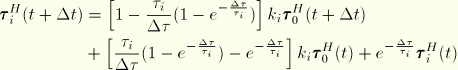
![]()

The internal deviatoric stresses ![]() at time
at time ![]() follow from
follow from
Observe that
![]()
![]()
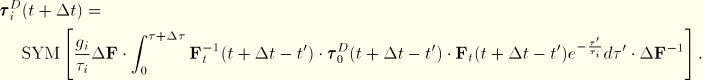
Now introduce the variable
Note that andThen we can also introduce
Substitution of Equation 4.8.2–5, Equation 4.8.2–12, and Equation 4.8.2–15 into Equation 4.8.2–11 yields
To integrate the first integral in Equation 4.8.2–16, we assume that ![]() varies linearly with the reduced time
varies linearly with the reduced time ![]() over the increment:
over the increment:
![]()
Equation 4.8.2–16 and Equation 4.8.2–17 for the deviatoric stress have exactly the same form as Equation 4.8.2–7 and Equation 4.8.2–8 for the hydrostatic stress. Hence, after integration we obtain
with![]()
The total stress at the end of the increment becomes
which with Equation 4.8.2–9 and Equation 4.8.2–18 can also be written as
To solve the system of nonlinear equations generated by the constitutive equations, we need to generate the corotational constitutive rate equations. From Equation 4.8.2–20 it follows
whereWith Equation 4.8.2–13 it follows that
where![]()
Using the definition of the corotational (Jaumann) rate, it follows that
whereEquation 4.8.2–21 then simplifies to

All equations have been worked out in terms of the Kirchhoff stress. However, the implementation in ABAQUS uses the Cauchy stress. To transform to Cauchy stress, we use the relations
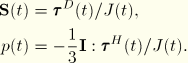
With ![]() , this allows us to write Equation 4.8.2–9, Equation 4.8.2–13, Equation 4.8.2–15, Equation 4.8.2–18, Equation 4.8.2–19, and Equation 4.8.2–27 in the following form:
, this allows us to write Equation 4.8.2–9, Equation 4.8.2–13, Equation 4.8.2–15, Equation 4.8.2–18, Equation 4.8.2–19, and Equation 4.8.2–27 in the following form:
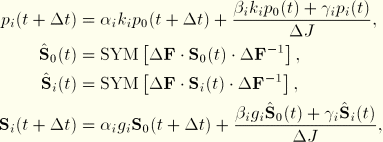
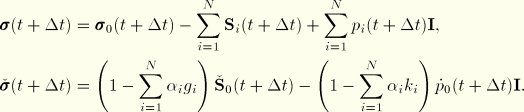
The virtual work and rate of virtual work equations are written with respect to the current volume. Therefore, the corotational stress rates are rates of Kirchhoff stress mapped into the current configuration and transformed in the same way as the stresses themselves.
This set of equations—combined with the expressions for ![]() ,
, ![]() , and
, and ![]() —describe the full implementation of the hyper-viscoelasticity model in a displacement formulation.
—describe the full implementation of the hyper-viscoelasticity model in a displacement formulation.
The rate equations can be written in a form similar to “Hyperelastic material behavior,” Section 4.6.1. Introduce
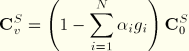
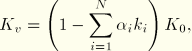

The in-plane deformation produces ![]() and
and ![]() , from which we can calculate only
, from which we can calculate only ![]() ,
, ![]() ,
, ![]() , and
, and ![]() .
. ![]() ,
, ![]() ,
, ![]() and
and ![]() are zero. The deformation in the third direction, characterized by
are zero. The deformation in the third direction, characterized by ![]() , is derived from the plane stress condition
, is derived from the plane stress condition
![]()
In this case ![]() or
or
![]()
The rate-independent constitutive equations, based on ![]() , produce
, produce
![]()
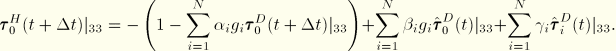
To obtain the rate equation, we use the linearized expression
![]()
In this case Equation 4.8.2–28 becomes an implicit equation in ![]() that needs to be solved iteratively. We use the Newton method, for which the first variation of
that needs to be solved iteratively. We use the Newton method, for which the first variation of ![]() with respect to
with respect to ![]() needs to be calculated
needs to be calculated
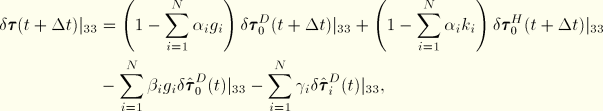
Similar to Equation 4.8.2–27, the last two terms vanish, which yields
whereIn the ABAQUS implementation we use Cauchy stresses instead of Kirchhoff stresses. The stresses can easily be mapped by dividing by J. Equation 4.8.2–28 and Equation 4.8.2–29 transform into
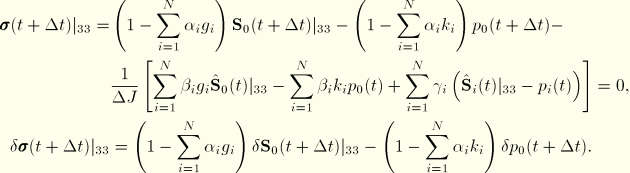
To obtain the rate equation, we use the constraint