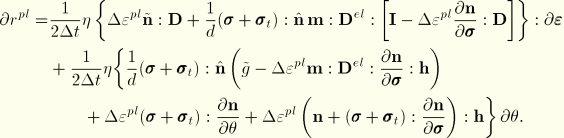4.3.10 Heat generation caused by plastic straining

Products: ABAQUS/Standard ABAQUS/Explicit

ABAQUS allows the introduction of the inelastic heat fraction, , which defines heat generation caused by mechanical dissipation associated with plastic straining. This term can be introduced as a source of coupling for thermal-mechanical analysis. Such coupling might be important in a simulation in which extensive inelastic deformation is occurring fairly rapidly in a material whose mechanical properties are temperature dependent. If the process is very slow, the heat generated by the plastic deformation has time to dissipate; and uncoupled, isothermal, analysis is sufficient to model the process. If the process is extremely rapid, the heat has no time to diffuse; and uncoupled, adiabatic, analysis (in which each integration point is treated as if it is thermally insulated from its neighbors) is sufficient. Fully coupled thermal-stress analysis is required for cases that lie far enough from both extremes. This section defines the heat generation term caused by inelastic straining and describes how this term contributes to the overall Newton solution scheme.

The model assumes that plastic straining gives rise to a heat flux per unit volume of

where

is the heat flux that is added into the thermal energy balance;

is the inelastic heat fraction, which is assumed to be a constant;

is the stress; and

is the rate of plastic straining. For all the plasticity models in ABAQUS, the plastic strain increment is written from the flow potential as

where

is the flow direction (we assume

, where

is the temperature) and

is a scalar measure of plastic straining that is used as a hardening parameter in the yield surface and flow potential definitions in some of the plasticity models. In this case we consider isotropic hardening theories only: ABAQUS provides only thermo-mechanical coupling for such models.

ABAQUS generally uses a backward Euler scheme to integrate the plastic strain, so at the end of the increment is approximated as

where all quantities are evaluated at the end of the increment (at time

) except

. This notation is adopted throughout the remainder of this section. This term is used as the contribution to the thermal energy balance equation.

When Newton's method is used to solve the nonlinear equations, the coupling term gives rise to three contributions to the Jacobian matrix for the Newton method:

from the thermal energy balance equation, and

from the mechanical equilibrium equation. The general form for these terms is now derived.

The mechanical constitutive model has the following general form. The elasticity defines the stresses by

where

is the strain energy density potential and

is the mechanical elastic strain. We implicitly assume that the elasticity is not fully incompressible, although the derivation is not significantly different if this is not the case, since the pressure stress will do no work in a fully incompressible material and so makes no contribution to the terms under discussion.

We assume that there is an additive strain rate decomposition that can be integrated to give

where

is the total strain and

is the strain caused by thermal expansion. In the constitutive models in ABAQUS

only. This form of decomposition of the deformation depends on

being measured as the integrated rate of deformation and on the elastic and thermal strains being small: this is true for the standard plasticity models provided in the program.

The plastic flow definition is integrated by the backward Euler method to give

Finally, assuming there is a single active yield surface or a single active flow surface, rate-independent models introduce a yield surface constraint, while rate-dependent models provide an integrated flow rate constraint, both of which are incorporated in the general form

where

is a scalar stress function (for example, the Mises or Hill stress function for simple metal plasticity models) and

is the yield stress for a rate-independent model, while

for a rate-dependent model, where

defines the rate effect from the average plastic strain rate over the increment. For example, by default, the rate-dependent plasticity model defines

where

is the Mises or Hill equivalent stress, and

and

are material parameters. Using the average plastic strain rate over the increment in this expression defines

Equation 4.3.10–1 to Equation 4.3.10–4 are a general definition of all of the standard isotropic hardening plasticity models integrated by the backward Euler method.

We now take variations of these equations with respect to all quantities at the end of the increment: