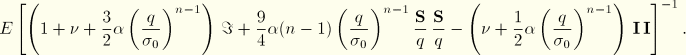Product: ABAQUS/Standard
Deformation plasticity theory is provided in ABAQUS/Standard to allow fully plastic analysis of ductile metals, usually under small-displacement conditions, for fracture mechanics applications. The model is based on the Ramberg-Osgood relationship. In this section the detailed constitutive model is defined. The procedure for obtaining fully plastic solutions generally consists of incremental loading until the response is fully plastic.
The model is termed deformation plasticity because the stress is defined by the total mechanical strain with no history dependence. There is no “unloading” criterion (to allow recovery of the initial elastic stiffness immediately after a strain reversal), so that the model is only useful as a plasticity model in cases of continuous flow. It is, in fact, a nonlinear elastic model; but at a limit state when all of a specimen or structure is responding plastically, this model is a useful equivalent representation of the plastic response because it has such a simple form.

The basic one-dimensional model is
whereThe material behavior described by this model is nonlinear at all stress levels, but for commonly used values of the hardening exponent (![]() or more) the nonlinearity becomes significant only at stress magnitudes approaching or exceeding
or more) the nonlinearity becomes significant only at stress magnitudes approaching or exceeding ![]() .
.

A linear “elastic” relation is used to generalize the first term of Equation 4.3.9–1; the nonlinear term is generalized to multiaxial stress states through the use of the Mises stress potential and associated flow law, giving the multiaxial model
where![]()
is the strain tensor,
![]()
is the stress tensor,
![]()
is the equivalent hydrostatic stress,
![]()
is the Mises equivalent stress,
![]()
is the stress deviator, and
![]()
is Poisson's ratio.
The linear part of the behavior may be compressible or incompressible depending on the value of Poisson's ratio, but the nonlinear part of the behavior is incompressible (because the flow is normal to the Mises stress potential). Since the model will generally be used for cases when the deformation is dominated by plastic flow, the use of selectively reduced integration elements or “hybrid” (mixed formulation) elements is recommended with this material model (except in plane stress).

The model is often used to obtain fully plastic solutions for fracture mechanics when the J-integral is needed. For evaluation of the J-integral the strain energy density is required. This is
![]()
![]()

During an analysis at each integration point the latest estimate of the kinematic solution is provided to the constitutive routines, which must provide the corresponding stress tensor calculated for the material model being used. Since this material model is nonlinear, we solve for the stresses by using the methods described below.
In this case
where nowWe solve Equation 4.3.9–3 for ![]() using Newton's method. Writing
using Newton's method. Writing ![]() as the correction to
as the correction to ![]() , the Newton equations for Equation 4.3.9–3 are
, the Newton equations for Equation 4.3.9–3 are
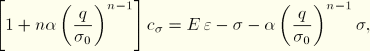
![]()
In this case the material stiffness matrix is
![]()
When all strain components are defined kinematically (that is, all cases except uniaxial and plane stress), projecting Equation 4.3.9–2 onto ![]() gives
gives
![]()
![]()
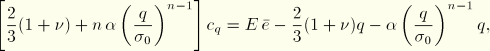
![]()
![]()
![]()
![]()
![]()
![]()
![]()
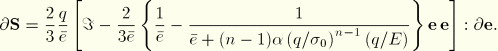
![]()
![]()
![]()
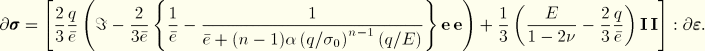
For this case we obtain a solution for ![]() assuming that the material is fully incompressible. We then use this solution as a starting guess for a Newton loop to find
assuming that the material is fully incompressible. We then use this solution as a starting guess for a Newton loop to find ![]() . Finally, we compute the corresponding material stiffness matrix.
. Finally, we compute the corresponding material stiffness matrix.
Incompressible approximation:
In this case ![]() and
and ![]() , so that
, so that ![]() is known and Equation 4.3.9–6 can be solved as before for q. Equation 4.3.9–7 then defines
is known and Equation 4.3.9–6 can be solved as before for q. Equation 4.3.9–7 then defines ![]() , and the plane stress constraint requires that
, and the plane stress constraint requires that ![]() , so
, so
![]()
![]()
![]()
![]()
Equation 4.3.9–2 defines the stresses, where, for this case,
![]()
![]()
![]()
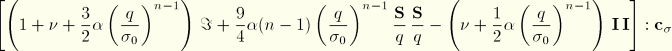
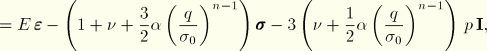
![]()