ABAQUS Theory Manual  


2.16.1 J-integral evaluation

Product: ABAQUS/Standard  

The J-integral is widely accepted as a fracture mechanics parameter for both linear and nonlinear material response. It is related to the energy release associated with crack growth and is a measure of the intensity of deformation at a notch or crack tip, especially for nonlinear materials. If the material response is linear, it can be related to the stress intensity factors. Because of the importance of the J-integral in the assessment of flaws, its accurate numerical evaluation is vital to the practical application of fracture mechanics in design calculations. ABAQUS/Standard provides a procedure for such evaluations of the J-integral, based on the virtual crack extension/domain integral methods (Parks, 1977, and Shih, Moran, and Nakamura, 1986). The method is particularly attractive because it is simple to use, adds little to the cost of the analysis, and provides excellent accuracy, even with rather coarse meshes.

J-integral in two dimensions

In the context of quasi-static analysis the J-integral is defined in two dimensions as

where is a contour beginning on the bottom crack surface and ending on the top surface, as shown in Figure 2.16.1–1; the limit indicates that shrinks onto the crack tip; is a unit vector in the virtual crack extension direction; and is the outward normal to . is given by

For elastic material behavior W is the elastic strain energy; for elastic-plastic or elastic-viscoplastic material behavior W is defined as the elastic strain energy density plus the plastic dissipation, thus representing the strain energy in an “equivalent elastic material.” This implies that the J-integral calculation is suitable only for monotonic loading of elastic-plastic materials.

Figure 2.16.1–1 Contour for evaluation of the J-integral.

Following Shih et al. (1986), we rewrite Equation 2.16.1–1 in the form

where is a sufficiently smooth weighting function within the region enclosed by the closed contour and has the value on and on C; and is the outward normal to the domain enclosed by the closed contour, as shown in Figure 2.16.1–2. on ; and is the surface traction on the crack surfaces and .

Figure 2.16.1–2 Closed contour encloses a domain A that includes the crack-tip region as

Using the divergence theorem, we convert the closed contour integral into the domain integral

where A is the domain enclosed by the closed contour . It is worth noting that the domain A includes the crack-tip region as .

If equilibrium is satisfied and W is a function of the mechanical strain—i.e., —we have

where is the body force per unit volume and is the thermal strain. Substituting the above two equations into Equation 2.16.1–3 gives

To evaluate these integrals, ABAQUS defines the domain in terms of rings of elements surrounding the crack tip. Different “contours” (domains) are created. The first contour consists of those elements directly connected to crack-tip nodes. The next contour consists of the ring of elements that share nodes with the elements in the the first contour as well as the elements in the first contour. Each subsequent contour is defined by adding the next ring of elements that share nodes with the elements in the previous contour. is chosen to have a magnitude of zero at the nodes on the outside of the contour and to be one (in the crack direction) at all nodes inside the contour except for the midside nodes (if they exist) in the outer ring of elements. These midside nodes are assigned a value between zero and one according to the position of the node on the side of the element.

J-integral in three dimensions

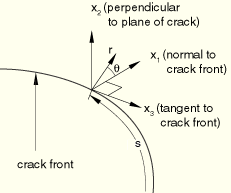
The J-integral can be extended to three dimensions by considering a crack with a tangentially continuous front, as shown in Figure 2.16.1–3. The local direction of virtual crack extension is again given by ,

Figure 2.16.1–3 Definition of local orthogonal Cartesian coordinates at the point s on the crack front; the crack is in the – plane.

which is perpendicular to the local crack front and lies in the crack plane. Asymptotically, as , the conditions for path independence apply on any contour in the – plane, which is perpendicular to the crack front at s. Hence, the J-integral defined in this plane can be extended to represent the pointwise energy release rate along the crack front as

For a virtual crack advance in the plane of a three-dimensional crack, the energy release rate is given by

where L denotes the crack front under consideration; is a surface element on a vanishingly small tubular surface enclosing the crack tip (i.e., ); and is the outward normal to . can be calculated by the domain integral method similar to that used in two dimensions. To do so, we first convert the surface integral in Equation 2.16.1–6 to a volume integral by introducing a contour surface , outside surface , external surfaces at the ends of the crack front (the surfaces vanish for the crack whose front forms a closed loop), and the crack faces , as shown in Figure 2.16.1–4.

Figure 2.16.1–4 Surface encloses a domain volume V that includes the crack-front region as

It can be seen that encloses a volume V. A weighting function is defined such that it has a magnitude of zero on and on . is assumed to vary smoothly between these values within A. On the external surfaces where is not tangential to the surfaces, it must be made so. This can be done in ABAQUS by defining the surface normals explicitly. Then, we can rewrite Equation 2.16.1–6 as

where is the outward normal to A (and on ). is the surface traction on surfaces and the crack surfaces .

Using the divergence theorem, we obtain

To obtain at each node set P along the crack front line, is discretized with the same interpolation functions as those used in the finite elements along the crack front:

where at the node set P and all other are zero. This expression for is substituted into Equation 2.16.1–8. Finally, the J-integral value at each node set P along the crack front can be calculated as

Reference