
Product: ABAQUS/Standard
This section describes the formulation used in the shell heat conduction elements in ABAQUS/Standard. The basis of the elements is a combination of piecewise quadratic interpolation of temperature through the thickness of the shell and either linear interpolation (in elements DS3 and DS4) or quadratic interpolation (in elements DS6 and DS8) on the reference surface of the shell. The isoparametric interpolation functions for the shell reference surface are identical in form to those used for the solid quadrilateral and triangular elements and can be found in “Solid isoparametric quadrilaterals and hexahedra,” Section 3.2.4, and “Triangular, tetrahedral, and wedge elements,” Section 3.2.6, respectively. Nodal temperature values are stored at a set of points through the thickness (points P below) at each node of the element (nodes N below). For the purpose of numerical integration of the finite element equations, a 2 × 2 Gauss integration scheme with a 2 × 2 nodal integration scheme for the internal energy and specific heat term is used for the quadrilateral element DS4 and a 3 × 3 Gauss integration scheme is used for the quadrilateral element DS8. Three- and six-point integration schemes are used for the triangular elements DS3 and DS6, respectively, the details of which can be found in “Triangular, tetrahedral, and wedge elements,” Section 3.2.6.
Let ![]() be material coordinates of a point in the reference surface of the shell, and let
be material coordinates of a point in the reference surface of the shell, and let ![]() measure position through the thickness of the shell so that
measure position through the thickness of the shell so that ![]() , where h is the thickness of the shell,
, where h is the thickness of the shell, ![]() is the offset of the reference surface from the midsurface as discussed in “Transverse shear stiffness in composite shells and offsets from the midsurface,” Section 3.6.8. The position of any point in the shell is given by
is the offset of the reference surface from the midsurface as discussed in “Transverse shear stiffness in composite shells and offsets from the midsurface,” Section 3.6.8. The position of any point in the shell is given by
![]()
![]()
is the position of a point in the reference surface, and
![]()
is the unit normal to the reference surface of the shell.
![]()
is a piecewise parabolic interpolation,
![]()
is an interpolator in the reference surface, and
![]()
are nodal temperature values (at node N, point P through the thickness).
The basic heat energy balance is Equation 2.11.1–3, with the approximate Jacobian matrix for the Newton method based on
![]()
The internal energy rate term (the first term in Equation 2.11.1–3) contributes, to the residual,
![]()
![]()
For the second term the temperature derivatives are taken with respect to a local orthogonal system ![]() , where
, where ![]() and
and ![]() measure distance along local base vectors
measure distance along local base vectors ![]() and
and ![]() , in the reference surface of the shell, set up according to the standard convention in ABAQUS for such local systems in shells. The term is formed by first introducing an intermediate set of temperature values,
, in the reference surface of the shell, set up according to the standard convention in ABAQUS for such local systems in shells. The term is formed by first introducing an intermediate set of temperature values,
![]()
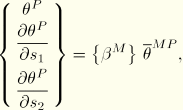
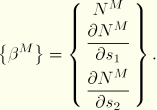
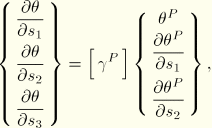
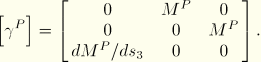
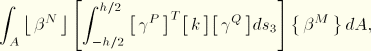
Finally, the external flux terms contribute
![]()
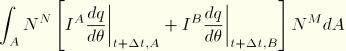
![]()
at point A through the thickness
![]()
at all other points through the thickness,