
Product: ABAQUS/Standard
The formulation in this section describes a capability for modeling heat transfer with convection in ABAQUS/Standard. The resulting elements can be used in any general heat transfer mesh. These elements have a nonsymmetric Jacobian matrix: the nonsymmetric capability is invoked automatically if elements of this type are included in the model. Both steady-state and transient capabilities are provided. The transient capability introduces a limit on the time increment (the limit is defined below): the time increment is adjusted to satisfy this limit if necessary. The steady-state versions of the elements can be used in a transient analysis, which means that transient effects in the fluid are not included in the model. The formulation is based on the work of Yu and Heinrich (1986, 1987).

The thermal equilibrium equation for a continuum in which a fluid is flowing with velocity ![]() , is
, is
![]()
The boundary conditions are that ![]() is prescribed over some part of the surface,
is prescribed over some part of the surface, ![]() , and that the heat flux per unit area entering the domain across the rest of the surface,
, and that the heat flux per unit area entering the domain across the rest of the surface, ![]() , is prescribed or is defined by convection and/or radiation conditions. For example, the boundary layer between fluid convection elements and solid elements might be modeled by DINTERx-type elements. The boundary term in the thermal equilibrium equation defines
, is prescribed or is defined by convection and/or radiation conditions. For example, the boundary layer between fluid convection elements and solid elements might be modeled by DINTERx-type elements. The boundary term in the thermal equilibrium equation defines
![]()
These equations are discretized with respect to position by using first-order isoparametric elements. The fluid velocity, ![]() , is assumed to be known. (ABAQUS actually requires that the mass flow rate of the fluid per unit area be defined, because this is generally more convenient for the user. The velocity is computed from the mass flow rate and the density of the fluid.)
, is assumed to be known. (ABAQUS actually requires that the mass flow rate of the fluid per unit area be defined, because this is generally more convenient for the user. The velocity is computed from the mass flow rate and the density of the fluid.)
The time discretization generates the solution at time ![]() from the known solution at time t.
from the known solution at time t.
The interpolation for the temperature, ![]() , is defined over an element and over a time increment as
, is defined over an element and over a time increment as
![]()
![]()
The Petrov-Galerkin discretization proposed by Yu and Heinrich couples this linear interpolation with the weighting functions

![]()
![]()
![]()
The characteristic element length measure, h, is defined by Yu and Heinrich as follows.
Let ![]() be the
be the ![]() isoparametric line across the element passing through its centroid. The projection of
isoparametric line across the element passing through its centroid. The projection of ![]() in the direction of the fluid velocity vector at the element's centroid is
in the direction of the fluid velocity vector at the element's centroid is
![]()
![]()
Since the weighting functions are biased (“upwinding”), they are discontinuous from one element to the next. Some care is, therefore, required in manipulating the weak form of the thermal equilibrium equation (see Hughes and Brooks, 1982). In particular, the usual integration by parts of the conduction term
![]()
![]()
The weak form of thermal equilibrium is
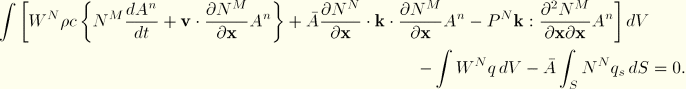


We now integrate this equation from time t to ![]() to provide an average equilibrium statement for the increment. We use the results
to provide an average equilibrium statement for the increment. We use the results
![]()
![]()
![]()

For the steady-state case the third term in this equation is omitted. In both transient and steady-state forms the contribution of such a convective element to the system of equations for the heat transfer model is not symmetric, requiring the use of the nonsymmetric matrix storage and solution scheme.