Products: ABAQUS/Standard ABAQUS/Explicit ABAQUS/CAE
Spring elements:
can couple a force with a relative displacement;
in ABAQUS/Standard can couple a moment with a relative rotation;
can be linear or nonlinear;
if linear, can be dependent on frequency in direct-solution steady-state dynamic analysis; and
can be dependent on temperature and field variables.
The terms “force” and “displacement” are used throughout the description of spring elements. When the spring is associated with displacement degrees of freedom, these variables are the force and relative displacement in the spring. If the springs are associated with rotational degrees of freedom, they are torsional springs; these variables will then be the moment transmitted by the spring and the relative rotation across the spring.
Viscoelastic spring behavior can be modeled in ABAQUS/Standard by combining frequency-dependent springs and frequency-dependent dashpots.
Spring elements are used to model actual physical springs as well as idealizations of axial or torsional components. They can also model restraints to prevent rigid body motion.
SPRING1 and SPRING2 elements are available only in ABAQUS/Standard. SPRING1 is between a node and ground, acting in a fixed direction. SPRING2 is between two nodes, acting in a fixed direction.
The SPRINGA element is available in both ABAQUS/Standard and ABAQUS/Explicit. SPRINGA acts between two nodes, with its line of action being the line joining the two nodes, so that this line of action can rotate in large-displacement analysis.
The spring behavior can be linear or nonlinear in any of the spring elements in ABAQUS.
Element types SPRING1 and SPRING2 can be associated with displacement or rotational degrees of freedom (in the latter case, as torsional springs). However, the use of torsional springs in large-displacement analysis requires careful consideration of the definition of total rotation at a node; therefore, connector elements (“Connectors: overview,” Section 17.1.1) are usually a better approach to providing torsional springs for large-displacement cases.
| Input File Usage: | Use the following option to specify a spring element between a node and ground, acting in a fixed direction: |
*ELEMENT, TYPE=SPRING1 Use the following option to specify a spring element between two nodes, acting in a fixed direction: *ELEMENT, TYPE=SPRING2 Use the following option to specify a spring element between two nodes with its line of action being the line joining the two nodes: *ELEMENT, TYPE=SPRINGA |
| ABAQUS/CAE Usage: | Property or Interaction module: Special |
A SPRINGA element introduces a stiffness between two degrees of freedom without introducing an associated mass. In an explicit dynamic procedure this represents an unconditionally unstable element. The nodes to which the spring is attached must have some mass contribution from adjacent elements; if this condition is not satisfied, ABAQUS/Explicit will issue an error message. If the spring is not too stiff (relative to the stiffness of the adjacent elements), the stable time increment determined by the explicit dynamics procedure (“Explicit dynamic analysis,” Section 6.3.3) will suffice to ensure stability of the calculations.
ABAQUS/Explicit does not use the springs in the determination of the stable time increment. During the data check phase of the analysis, ABAQUS/Explicit computes the minimum of the stable time increment for all the elements in the mesh except the spring elements. The program then uses this minimum stable time increment and the stiffness of each of the springs to determine the mass required for each spring to give the same stable time increment. If this mass is too large compared to the mass of the model, ABAQUS/Explicit will issue an error message that the spring is too stiff compared to the model definition.
The relative displacement definition depends on the element type.
The relative displacement across a SPRING1 element is the ith component of displacement of the spring's node:
The relative displacement across a SPRING2 element is the difference between the ith component of displacement of the spring's first node and the jth component of displacement of the spring's second node:
It is important to understand how the SPRING2 element will behave according to the above relative displacement equation since the element can produce counterintuitive results. For example, a SPRING2 element set up in the following way will be a “compressive” spring:
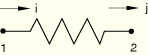
If the nodes displace so that 
and 
, the spring appears to be in compression, while the force in the SPRING2 element is positive. To obtain a “tensile” spring, the SPRING2 element should be set up in the following way:
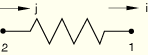
For geometrically linear analysis the relative displacement is measured along the direction of the SPRINGA element in the reference configuration:
is the reference position of the first node of the spring and 
is the reference position of its second node.For geometrically nonlinear analysis the relative displacement across a SPRINGA element is the change in length in the spring between the initial and the current configuration:
is the current length of the spring and 
is the value of 
in the initial configuration. Here 
and 
are the current positions of the nodes of the spring.In either case the force in a SPRINGA element is positive in tension.
The spring behavior can be linear or nonlinear. In either case you must associate the spring behavior with a region of your model.
| Input File Usage: | *SPRING, ELSET=name |
| where the ELSET parameter refers to a set of spring elements. |
| ABAQUS/CAE Usage: | Property or Interaction module: Special |
You define linear spring behavior by specifying a constant spring stiffness (force per relative displacement).
The spring stiffness can depend on temperature and field variables. See “Input syntax rules,” Section 1.2.1, for further information about defining data as functions of temperature and independent field variables.
For direct-solution steady-state dynamic analysis the spring stiffness can depend on frequency, as well as on temperature and field variables. If a frequency-dependent spring stiffness is specified for any other analysis procedure in ABAQUS/Standard, the data for the lowest frequency given will be used.
| Input File Usage: | *SPRING, DEPENDENCIES=n first data line spring stiffness, frequency, temperature, field variable 1, etc. ... |
| ABAQUS/CAE Usage: | Property or Interaction module: Special |
| Defining the spring stiffness as a function of frequency, temperature, and field variables is not supported in ABAQUS/CAE when you define springs as engineering features; instead, you can define connectors that have spring-like elastic behavior (see “Connector elastic behavior,” Section 17.2.2). |
You define nonlinear spring behavior by giving pairs of force–relative displacement values. These values should be given in ascending order of relative displacement and should be provided over a sufficiently wide range of relative displacement values so that the behavior is defined correctly. ABAQUS assumes that the force remains constant (which results in zero stiffness) outside the range given (see Figure 18.1.1–1).
Initial forces in nonlinear springs should be defined as part of the 
relationship by giving a nonzero force, 
, at zero relative displacement.
The spring stiffness can depend on temperature and field variables. See “Input syntax rules,” Section 1.2.1, for further information about defining data as functions of temperature and independent field variables.
| Input File Usage: | *SPRING, NONLINEAR, DEPENDENCIES=n first data line force, relative displacement, temperature, field variable 1, etc. ... |
| ABAQUS/CAE Usage: | Defining nonlinear spring behavior is not supported in ABAQUS/CAE when you define springs as engineering features; instead, you can define connectors that have spring-like elastic behavior (see “Connector elastic behavior,” Section 17.2.2). |
You define the direction of action for SPRING1 and SPRING2 elements by giving the degree of freedom at each node of the element. This degree of freedom may be in a local coordinate system (“Orientations,” Section 2.2.5). The local system is assumed to be fixed: even in large-displacement analysis SPRING1 and SPRING2 elements act in a fixed direction throughout the analysis.
| Input File Usage: | *SPRING, ORIENTATION=name dof at node 1, dof at node 2 |
| ABAQUS/CAE Usage: | Property or Interaction module: Special |
Springs/Dashpots