Product: ABAQUS/Standard
Many applications of elastomers involve dynamic loading in the form of steady-state vibration, and often in such cases the dissipative losses in the material (the “viscous” part of the material's viscoelastic behavior) must be modeled to obtain useful results. In most problems of this class the structure is first preloaded statically, and this preloading generally involves large deformation of the elastomers. The response to that preloading is computed on the basis of purely elastic behavior in the elastomeric parts of the model—that is, we assume that the preloading is applied for a sufficiently long time so that any viscous response in the material has time to decay away.
The dynamic analysis problem in this case is, therefore, to investigate the dynamic, viscoelastic response about a predeformed elastic state. In some such cases we can reasonably assume that the vibration amplitude is sufficiently small that both the kinematic and material response in the dynamic phase of the problem can be treated as linear perturbations about the predeformed state. The small amplitude viscoelastic vibration capability provided in ABAQUS/Standard, which is described in Morman and Nagtegaal (1983) and uses the procedure described in “Direct steady-state dynamic analysis,” Section 2.6.1, is based on such a linearization. Its appropriateness to a particular application will depend on the magnitude of the vibration with respect to possible kinematic nonlinearities (the additional strains and rotations that occur during the dynamic loading must be small enough so that the linearization of the kinematics is reasonable) and with respect to possible nonlinearities in the material response, and on the particular constitutive assumptions incorporated in the viscoelastic model described in this section—in particular, the assumption of separation of prestrain and time effects described below.
In “Hyperelastic material behavior,” Section 4.6.1, it is shown that the rate of change of the true (Cauchy) stress in an elastomeric material with a strain energy potential is given by
for the deviatoric part of the stress andfor the equivalent pressure stress in a compressible material. The various quantities in these equations are defined in “Hyperelastic material behavior,” Section 4.6.1. For a fully incompressible material all components of
are zero and the equivalent pressure stress is defined only by the loading of the structure, so that the second equation is not applicable.For small viscoelastic vibrations about a predeformed state we linearize the additional motions that occur during the vibration so that the differential of a quantity in Equation 4.8.3–1 and Equation 4.8.3–2 can be interpreted as the additional incremental value,
, where 
is the current value of at some time during the vibration and 
is the reference value of ; that is, is the value of at the end of the static (long term) preloading, about which is fluctuating during the vibration.The incremental elastic constitutive behavior for small added motions defined by this interpretation of Equation 4.8.3–1 and Equation 4.8.3–2 is now generalized to include viscous dissipation as well as elastic response in the material, following Lianis (1965), to give
In these expressions 
is meant to indicate that depends on the elastic predeformation that has occurred prior to the small dynamic vibrations (the state at 
) and is evaluated at time 
, between the start of the vibrations and the current time, 
. 
and 
are the functions that define the viscous part of the material's response: the notation is intended to imply that these are functions of the elastic predeformation and time. 
is the time rate of change of a quantity.
The definitions of the viscous parts of the behavior, and , provided in ABAQUS are simplified by assuming that this viscous behavior exhibits separation of time and prestrain effects; that is, that
and 
are the “effective elasticity” of the material in its predeformed state, prior to the vibration. This assumption simply means that measurements of the viscous behavior during small motions of the material about a predeformed state depend only on the predeformation to the extent that the effective elasticity of the material also depends on that predeformation. There is experimental evidence that this simplification is appropriate for some practical materials (see Morman's (1979) discussion). With this assumption the definition of the viscous part of the material's behavior is reduced to finding the scalar functions of time, 
and 
(only for fully incompressible materials), and the constitutive response to small perturbations is simplified to
In ABAQUS this model is provided only for the direct-solution and subspace-based steady-state dynamic analysis procedures, in which we assume that the dynamic response is steady-state harmonic vibration, so that we can write
is the complex amplitude of a variable .Defining the Fourier transforms of the viscous relaxation functions 
and 
as
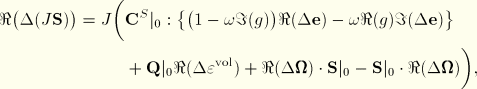
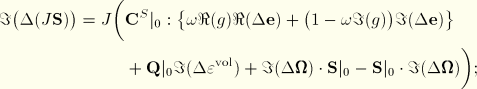
The viscous behavior of the material is, thus, reduced to defining 
, 
, 
, and 
as functions of frequency.
When the pure displacement formulation is used for a compressible material, the virtual work equation for dynamic response is
where
is the mass density of the material in the original configuration), and
per current surface area and body forces 
per current volume.For the linearized perturbations considered here we recast Equation 4.8.3–3 in incremental form, giving
where
is obtained from Equation 4.6.1–12 with the interpretation 
;
and are the externally prescribed tractions, so that 
and 
are externally prescribed traction increments. Note that 
includes terms dependent on 
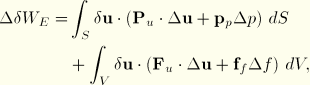
: these give rise to the “load stiffness matrix” when the finite element interpolations are introduced.When the motion is harmonic we can recast these quantities as
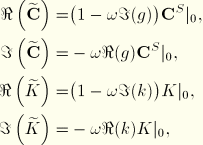
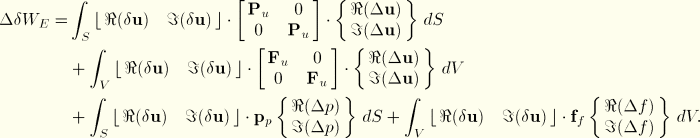
In these expressions 
and 
are understood to be independent variations. Thus, when the finite element displacement interpolations are introduced into Equation 4.8.3–4, we obtain a linear, frequency-dependent system that can be solved at each frequency for the real and imaginary parts of the nodal degrees of freedom of the model. In like fashion, the augmented variational principles for almost incompressible behavior and for fully incompressible behavior described in “Hyperelastic material behavior,” Section 4.6.1, can be used to obtain linear, frequency dependent systems for harmonic viscoelastic vibration problems. The steady-state dynamic analysis procedure based on modal superposition cannot be used because the viscous behavior assumed does not correspond to a small amount of Rayleigh damping, which is a requirement for steady-state harmonic response based on modal superposition.
