
Products: ABAQUS/Standard ABAQUS/Explicit
The constitutive behavior of a hyperelastic material is defined as a total stress–total strain relationship, rather than as the rate formulation that has been discussed in the context of history-dependent materials in previous sections of this chapter. Therefore, the basic development of the formulation for hyperelasticity is somewhat different. Furthermore, hyperelastic materials are often incompressible or very nearly so; hence, mixed (“hybrid”) formulations can be used effectively. In this section the hyperelastic model provided in ABAQUS is defined, and the mixed variational principles used in ABAQUS/Standard to treat the fully incompressible case and the almost incompressible case are introduced.

We first introduce some definitions and basic kinematic results that will be used in this section. Some of these items have already been discussed in Chapter 1, “Introduction and Basic Equations”: they are repeated here for convenience.
Writing the current position of a material point as ![]() and the reference position of the same point as
and the reference position of the same point as ![]() , the deformation gradient is
, the deformation gradient is
![]()
![]()
![]()
We then introduce the deviatoric stretch matrix (the left Cauchy-Green strain tensor) of ![]() as
as
![]()
The gradient of the displacement variation with respect to current position is written as
![]()
The virtual rate of deformation is the symmetric part of ![]() :
:
![]()
![]()
![]()
The virtual rate of spin of the material is the antisymmetric part of ![]() :
:
![]()
The variations of ![]() ,
, ![]() ,
, ![]() ,
, ![]() , and
, and ![]() are obtained directly from their definitions above in terms of these quantities as
are obtained directly from their definitions above in terms of these quantities as
![]()
![]()
![]()
![]()
The Cauchy (“true”) stress components are defined from the strain energy potential as follows. From the virtual work principal the internal energy variation is
![]()
We decompose the stress into the equivalent pressure stress,
![]()
![]()
![]()
For isotropic, compressible materials the strain energy, ![]() , is a function of
, is a function of ![]() ,
, ![]() , and
, and ![]() :
:
![]()
![]()
Since the variation of the strain energy potential is, by definition, the internal virtual work per reference volume, ![]() , we have
, we have
For a compressible material the strain variations are arbitrary, so this equation defines the stress components for such a material as
andWhen the material response is almost incompressible, the pure displacement formulation, in which the strain invariants are computed from the kinematic variables of the finite element model, can behave poorly. One difficulty is that from a numerical point of view the stiffness matrix is almost singular because the effective bulk modulus of the material is so large compared to its effective shear modulus, thus causing difficulties with the solution of the discretized equilibrium equations. Similarly, in ABAQUS/Explicit the high bulk modulus increases the dilatational wave speed, thus reducing the stable time increment substantially. Another problem is that, unless reduced-integration techniques are used, the stresses calculated at the numerical integration points show large oscillations in the pressure stress values, because—in general—the elements cannot respond accurately and still have small volume changes at all numerical integration points. To avoid such problems, ABAQUS/Standard offers a “mixed” formulation for such cases. The concept is to introduce a variable, ![]() , that is used in place of the volume change,
, that is used in place of the volume change, ![]() , in the definition of the strain energy potential. The internal energy integral,
, in the definition of the strain energy potential. The internal energy integral, ![]() , is augmented with the constraint that
, is augmented with the constraint that ![]() , imposed by the use of a Lagrange multiplier,
, imposed by the use of a Lagrange multiplier, ![]() , and integrated over the volume:
, and integrated over the volume:
![]()
![]()
![]()
![]()
![]()
This augmented formulation can be used for any value of compressibility except fully incompressible behavior. ![]() is interpolated independently in each element: ABAQUS uses constant
is interpolated independently in each element: ABAQUS uses constant ![]() in first-order elements and linear variation of
in first-order elements and linear variation of ![]() with respect to position in second-order elements, which implies that
with respect to position in second-order elements, which implies that ![]() is discontinuous between elements: continuity in such variables is not a requirement.
is discontinuous between elements: continuity in such variables is not a requirement.
When the material is fully incompressible, ![]() is a function of the first and second strain invariants—
is a function of the first and second strain invariants—![]() and
and ![]() —only, and we write the internal energy in the augmented form,
—only, and we write the internal energy in the augmented form,
![]()

The rate of change of the internal virtual work is required for use in the Newton method, which is generally used in ABAQUS/Standard to solve the nonlinear equilibrium equations (after discretization by finite elements). It will also be used when we extend the elasticity model to viscoelastic behavior for small (linearized) vibrations about a predeformed state.
When the pure displacement formulation is used for the compressible case, the deviatoric stress components, ![]() , are defined by Equation 4.6.1–8, from which we can show that
, are defined by Equation 4.6.1–8, from which we can show that
![]()
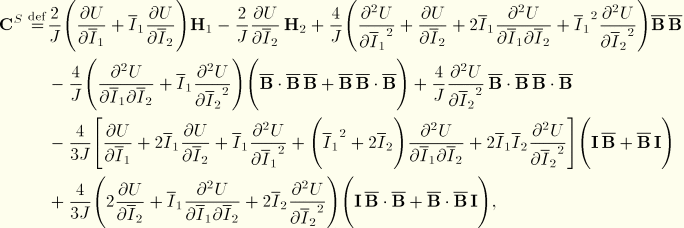
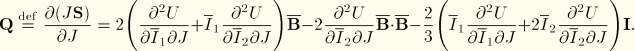
From Equation 4.6.1–9 it can be shown that
![]()
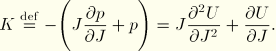
![]()
For the mixed formulation introduced for almost incompressible materials, the rate of change of the augmented variation of internal energy, Equation 4.6.1–10, is
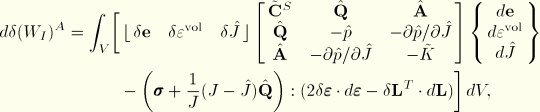
![]()
![]()
![]()
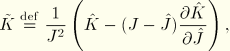
![]()
For the case of incompressible materials the rate of change of the augmented variation of internal energy is similarly obtained from Equation 4.6.1–11 as


Several particular forms of the strain energy potential are available in ABAQUS. The incompressible or almost incompressible models make up:
the polynomial form and its particular cases—the reduced polynomial form, the neo-Hookean form, the Mooney-Rivlin form, and the Yeoh form;
the Ogden form;
the Arruda-Boyce form; and
the Van der Waals form.
Given isotropy and additive decomposition of the deviatoric and volumetric strain energy contributions in the presence of incompressible or almost incompressible behavior, we can write the potential, in general, as
![]()
![]()
![]()
The ![]() values determine the compressibility of the material: if all the
values determine the compressibility of the material: if all the ![]() are zero, the material is taken as fully incompressible. If
are zero, the material is taken as fully incompressible. If ![]() , all
, all ![]() must be zero.
must be zero.
Regardless of the value of ![]() , the initial shear modulus,
, the initial shear modulus, ![]() and the bulk modulus,
and the bulk modulus, ![]() depend only on the polynomial coefficients of order
depend only on the polynomial coefficients of order ![]() :
:
![]()
If ![]() , so that only the linear terms in the deviatoric strain energy are retained, the Mooney-Rivlin form is recovered:
, so that only the linear terms in the deviatoric strain energy are retained, the Mooney-Rivlin form is recovered:
![]()
Particular forms of the polynomial model can also be obtained by setting specific coefficients to zero. If all ![]() with
with ![]() are set to zero, the reduced polynomial form is obtained:
are set to zero, the reduced polynomial form is obtained:
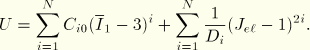
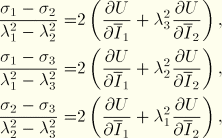
Measurements of the ![]() -dependence of carbon-black reinforced rubber vulcanizates confirming these findings can be found in Kawabata, Yamashita, et al. (1995). The paper of Kaliske and Rothert (1997) also supports the notion that often the prediction of general deformation states based on a uniaxial measurement can be enhanced only by ignoring the
-dependence of carbon-black reinforced rubber vulcanizates confirming these findings can be found in Kawabata, Yamashita, et al. (1995). The paper of Kaliske and Rothert (1997) also supports the notion that often the prediction of general deformation states based on a uniaxial measurement can be enhanced only by ignoring the ![]() -dependence.
-dependence.
In this context it is worth noting that the mathematical structure of the Arruda-Boyce model can be viewed as a fifth-order reduced polynomial, where the five coefficients ![]() are implicit nonlinear functions of the two parameters
are implicit nonlinear functions of the two parameters ![]() and
and ![]() in the Arruda-Boyce form. However, the Arruda-Boyce model offers a physical interpretation of the parameters, which the general fifth-order reduced polynomial fails to provide.
in the Arruda-Boyce form. However, the Arruda-Boyce model offers a physical interpretation of the parameters, which the general fifth-order reduced polynomial fails to provide.
The Yeoh form (Yeoh, 1993) can be viewed as a special case of the reduced polynomial with ![]() :
:
![]()
If the reduced-polynomial strain-energy function is simplified further by setting ![]() , the neo-Hookean form is obtained:
, the neo-Hookean form is obtained:
![]()
The user can request that ABAQUS calculate the ![]() and
and ![]() values from measurements of nominal stress and strain in simple experiments. The basis of this calculation is described in “Fitting of hyperelastic and hyperfoam constants,” Section 4.6.2.
values from measurements of nominal stress and strain in simple experiments. The basis of this calculation is described in “Fitting of hyperelastic and hyperfoam constants,” Section 4.6.2.
The Ogden strain energy potential is expressed in terms of the principal stretches. In ABAQUS the following formulation is used:
where![]()
The value of ![]() and tables giving the
and tables giving the ![]() and
and ![]() values as functions of temperature are specified by the user. If
values as functions of temperature are specified by the user. If ![]() ,
, ![]() , and
, and ![]() , the Mooney-Rivlin model is obtained. If
, the Mooney-Rivlin model is obtained. If ![]() and
and ![]() , Ogden's model degenerates to the neo-Hookean material model. In the Ogden form the initial shear modulus,
, Ogden's model degenerates to the neo-Hookean material model. In the Ogden form the initial shear modulus, ![]() , depends on all coefficients:
, depends on all coefficients:
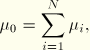
The hyperelastic Arruda-Boyce potential has the following form:
![]()
![]()
![]()
The initial bulk modulus is obtained as ![]() . To the deviatoric part of the strain energy density we add a simplified representation of the volumetric strain energy density, which requires only one material parameter, so that all material parameters can be estimated easily even with limited knowledge of the material behavior. This volumetric representation has been used successfully by Kaliske and Rothert (1997) and provides sufficient accuracy for most engineering elastomeric materials.
. To the deviatoric part of the strain energy density we add a simplified representation of the volumetric strain energy density, which requires only one material parameter, so that all material parameters can be estimated easily even with limited knowledge of the material behavior. This volumetric representation has been used successfully by Kaliske and Rothert (1997) and provides sufficient accuracy for most engineering elastomeric materials.
The Arruda-Boyce potential depends on the first invariant only. The physical interpretation is that the eight chains are stretched equally under the action of a general deformation state. The first invariant, ![]() , directly represents this elongation.
, directly represents this elongation.
When the Arruda-Boyce form is chosen, the user can specify the coefficients as functions of temperature; alternatively, ABAQUS can perform a fit of the test data specified by the user to determine the coefficients.
The hyperelastic Van der Waals potential, also known as the Kilian model, has the following form:
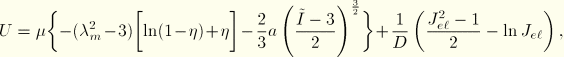

The locking stretch, ![]() , accounts for finite extendability of the non-Gaussian chain network. In contrast to the Arruda-Boyce model the mathematical structure of the Van der Waals potential is such that the strain energy tends to infinity as the locking stretch,
, accounts for finite extendability of the non-Gaussian chain network. In contrast to the Arruda-Boyce model the mathematical structure of the Van der Waals potential is such that the strain energy tends to infinity as the locking stretch, ![]() , is reached; more precisely, as
, is reached; more precisely, as ![]() . Thus, the Van der Waals potential cannot be used at stretches larger than the locking stretch.
. Thus, the Van der Waals potential cannot be used at stretches larger than the locking stretch.
The global interaction parameter, ![]() , models the interaction between the chains; it is difficult to estimate. Kilian et al. (1986) point out that, given Mooney-Rivlin coefficients and a locking stretch
, models the interaction between the chains; it is difficult to estimate. Kilian et al. (1986) point out that, given Mooney-Rivlin coefficients and a locking stretch ![]() , a suitable value for the global interaction parameter is
, a suitable value for the global interaction parameter is
![]()
The parameter ![]() represents a linear mixture parameter combining both invariants
represents a linear mixture parameter combining both invariants ![]() and
and ![]() into
into ![]() ; for
; for ![]() , the Van der Waals potential will be dependent on the first invariant only. Admissible values for this parameter are
, the Van der Waals potential will be dependent on the first invariant only. Admissible values for this parameter are ![]() .
.
When the Van der Waals potential is chosen, the user can specify the coefficients as functions of temperature; alternatively, the parameters can be fitted from user-defined test data. The data fitting procedure will not necessarily yield a value of ![]() between zero and one. If during the curve fitting procedure the parameter
between zero and one. If during the curve fitting procedure the parameter ![]() leaves the admissible range, the curve fitting procedure is aborted and restarted with a fixed value of
leaves the admissible range, the curve fitting procedure is aborted and restarted with a fixed value of ![]() . Alternatively, the curve fitting procedure can be used with a user-defined value of
. Alternatively, the curve fitting procedure can be used with a user-defined value of ![]() .
.
While the previous forms are intended for incompressible or almost incompressible materials, the elastic foam energy function is designed for describing highly compressible elastomers (Storåkers, 1986). This energy function has the form
where![]()
![]()
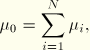
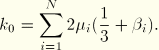
If Poisson's ratio is constant and known, ABAQUS can calculate the ![]() and
and ![]() from measurements of nominal stress and stretch as before. If Poisson's ratio depends on the level of straining, ABAQUS can also calculate the
from measurements of nominal stress and stretch as before. If Poisson's ratio depends on the level of straining, ABAQUS can also calculate the ![]() from the nominal lateral strains.
from the nominal lateral strains.