
Products: ABAQUS/Standard ABAQUS/Explicit
In this section we will derive the equations needed for fitting the hyperelastic (polynomial, Ogden, Arruda-Boyce, and Van der Waals form) and hyperfoam constants to experimental test data. In addition, the procedures for checking the material stability using the Drucker criterion will be described.
For the hyperelastic models full incompressibility is assumed in fitting the hyperelastic constants to the test data, except in the volumetric test.

The hyperelastic polynomial form can be fitted by ABAQUS up to order ![]() . Since the Mooney-Rivlin potential corresponds to the case
. Since the Mooney-Rivlin potential corresponds to the case ![]() , these remarks also apply by setting the higher-order coefficients to zero. The energy potential is as follows:
, these remarks also apply by setting the higher-order coefficients to zero. The energy potential is as follows:
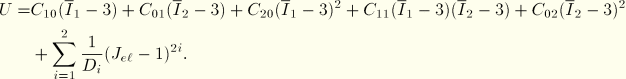
The deformation modes are characterized in terms of the principal stretches. The nominal stress-strain relations are now derived for the polynomial form with ![]() .
.

The hyperelastic reduced polynomial form can be fitted by ABAQUS up to order ![]() . For
. For ![]() the reduced polynomial is identical to the Yeoh model, and for
the reduced polynomial is identical to the Yeoh model, and for ![]() the neo-Hookean model is retained; hence, the following also applies to these forms. The reduced polynomial energy potential is as follows:
the neo-Hookean model is retained; hence, the following also applies to these forms. The reduced polynomial energy potential is as follows:
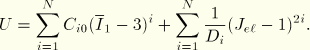

The hyperelastic Ogden form can be fitted up to order ![]() :
:
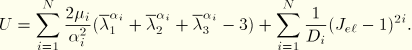

The hyperelastic Arruda-Boyce potential has the following form:
![]()
![]()

The hyperelastic Van der Waals potential, also known as the Kilian model, has the following form:
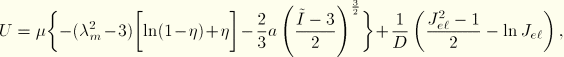

Following the same approach as for the polynomial form, we can derive the nominal stress-strain relations for the Van der Waals form.

The hyperfoam potential is a modified form of the Hill strain energy potential and can be fitted up to order ![]() :
:
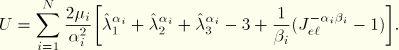
The deformation modes are characterized in terms of the principal stretches and the volume ratio ![]() . The elastomeric foams are not incompressible:
. The elastomeric foams are not incompressible: ![]() . The transverse stretches
. The transverse stretches ![]() and/or
and/or ![]() are independently specified in the test data either as individual values depending on the lateral deformations or through the definition of an effective Poisson's ratio.
are independently specified in the test data either as individual values depending on the lateral deformations or through the definition of an effective Poisson's ratio.
![]()
The common nominal stress-strain relation for the three deformation modes above is

The simple shear deformation is described in terms of the deformation gradient,
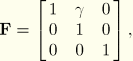
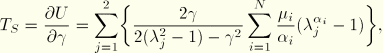
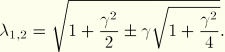
The transverse stress ![]() developed during simple shear deformation (as a result of the Poynting effect) is
developed during simple shear deformation (as a result of the Poynting effect) is
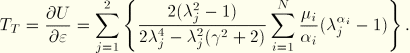

Given experimental data, the material constants are determined through a least-squares-fit procedure, which minimizes the relative error in stress. For the ![]() nominal stress–nominal strain data pairs, the relative error measure
nominal stress–nominal strain data pairs, the relative error measure ![]() is minimized,
is minimized,
![]()
The polynomial potential is linear in terms of the constants ![]() ; therefore, a linear least-squares procedure can be used. The Ogden, the Arruda-Boyce, and the Van der Waals potential are nonlinear in some of their coefficients, thus necessitating the use of a nonlinear least-squares procedure.
; therefore, a linear least-squares procedure can be used. The Ogden, the Arruda-Boyce, and the Van der Waals potential are nonlinear in some of their coefficients, thus necessitating the use of a nonlinear least-squares procedure.

For the full polynomial model we can rewrite the expressions for the ![]() derived above as
derived above as
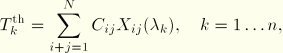
![]()
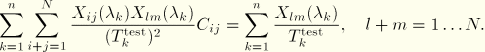
To fit the volumetric coefficients, one needs to solve the system of ![]() equations
equations
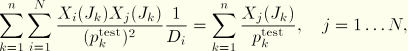
![]()
![]()

For the reduced polynomial model we can rewrite the expressions for ![]() derived above as follows:
derived above as follows:
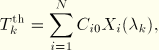
Following the same arguments as for the full polynomial, we arrive at the system of ![]() equations
equations
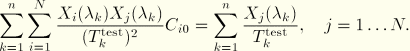

The Ogden, Arruda-Boyce, and Van der Waals potentials are nonlinear in some of their coefficients; hence, a nonlinear least-squares-fit procedure is required. We use the Marquard-Levenberg algorithm in the formulation by Twizell and Ogden (1986). Let ![]() ,
, ![]() be the coefficients of these hyperelastic models, where
be the coefficients of these hyperelastic models, where ![]() is the number of coefficients contributing to the deviatoric behavior. Specifically,
is the number of coefficients contributing to the deviatoric behavior. Specifically, ![]() for the Ogden model,
for the Ogden model, ![]() for the Arruda-Boyce model, and
for the Arruda-Boyce model, and ![]() for the Van der Waals model. The coefficients are found by iterating the equation
for the Van der Waals model. The coefficients are found by iterating the equation

![]()
![]()
For ![]() , the Newton algorithm is obtained; for very large values of
, the Newton algorithm is obtained; for very large values of ![]() , the steepest descent method is obtained. Thus, the Marquard-Levenberg algorithm represents a compromise between these two approaches: the value of
, the steepest descent method is obtained. Thus, the Marquard-Levenberg algorithm represents a compromise between these two approaches: the value of ![]() is increased if the error grows and is reduced otherwise.
is increased if the error grows and is reduced otherwise.

After initializing the ![]() , the parameters
, the parameters ![]() are found with a linear least squares fit. In the iterative procedure outlined above, the following derivatives are used:
are found with a linear least squares fit. In the iterative procedure outlined above, the following derivatives are used:
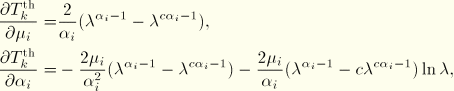
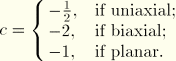

The Arruda-Boyce model is linear in the shear modulus ![]() but nonlinear in the locking stretch
but nonlinear in the locking stretch ![]() . The locking stretch is initialized as
. The locking stretch is initialized as ![]() , where
, where ![]() is the maximum stretch in the user-specified test data. Given this locking stretch, the initial shear modulus,
is the maximum stretch in the user-specified test data. Given this locking stretch, the initial shear modulus, ![]() , is obtained with a linear least squares fit.
, is obtained with a linear least squares fit.
In the iterative procedure outlined above, the following derivatives are used:
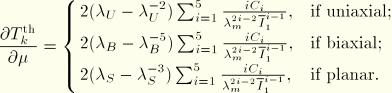
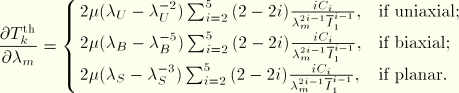

The Van der Waals model is linear in the shear modulus ![]() but nonlinear in the locking stretch
but nonlinear in the locking stretch ![]() , the global interaction parameter
, the global interaction parameter ![]() , and the mixture parameter
, and the mixture parameter ![]() . The locking stretch is initialized as
. The locking stretch is initialized as ![]() , where
, where ![]() is the maximum stretch in the user-specified test data. Given this guess for the locking stretch, we make use of an expression proposed by Kilian et al. (1986) to initialize the global interaction parameter
is the maximum stretch in the user-specified test data. Given this guess for the locking stretch, we make use of an expression proposed by Kilian et al. (1986) to initialize the global interaction parameter
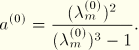
In the iterative procedure outlined above, the following derivatives are used:
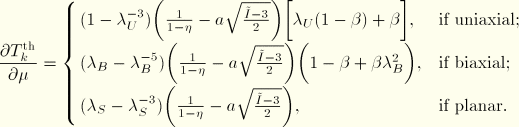
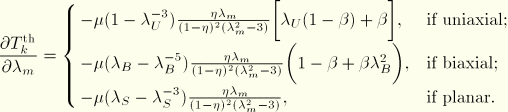
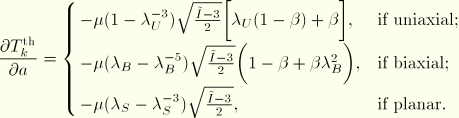

In the derivatives of ![]()
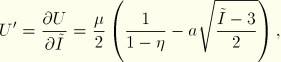
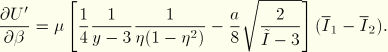
In the planar case ![]() ; hence,
; hence, ![]() vanishes.
vanishes.

ABAQUS checks the Drucker stability of the material for the first three modes of deformation described above. The Drucker stability condition requires that the change in the Kirchhoff stress ![]() following from an infinitesimal change in the logarithmic strain
following from an infinitesimal change in the logarithmic strain ![]() satisfies the inequality
satisfies the inequality
![]()
Using ![]() , the inequality becomes
, the inequality becomes
![]()
For the isotropic elastic formulation considered here, the inequality can be represented in terms of the principal stresses and strains:
![]()
With the incompressibility assumption for the two hyperelastic models, the Kirchhoff stress is equal to the Cauchy stress: ![]() and, thus,
and, thus,
![]()
![]()
![]()
The relation between changes in the stress and changes in strain are described by the matrix equation
![]()
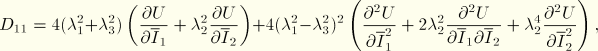
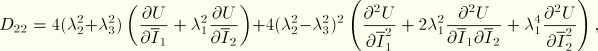
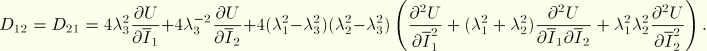
For material stability ![]() must be positive definite; thus, it is necessary that
must be positive definite; thus, it is necessary that
![]()
![]()
For the Ogden form we follow the same approach as the polynomial form. Using ![]() , we have
, we have
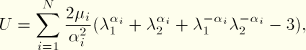
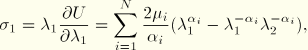
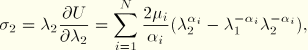
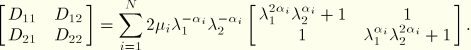
For positive values of the shear modulus, ![]() , and the locking stretch,
, and the locking stretch, ![]() , the Arruda-Boyce form is always stable. Hence, it suffices to check the coefficients to determine whether the material satisfies Drucker stability.
, the Arruda-Boyce form is always stable. Hence, it suffices to check the coefficients to determine whether the material satisfies Drucker stability.
When the Van der Waals model is employed in its admissible stretch range given by ![]() , its stability depends on the global interaction parameter,
, its stability depends on the global interaction parameter, ![]() , for positive values of the initial shear modulus,
, for positive values of the initial shear modulus, ![]() , and the locking stretch,
, and the locking stretch, ![]() . To verify the Drucker stability of the Van der Waals model, we can employ the equations derived for the polynomial models by making use of the fact that
. To verify the Drucker stability of the Van der Waals model, we can employ the equations derived for the polynomial models by making use of the fact that
![]()
![]()
The Kirchhoff stress-strain relation for the uniaxial, biaxial, planar, and volumetric deformation modes is
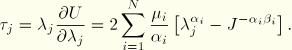
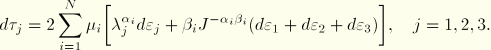
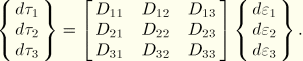
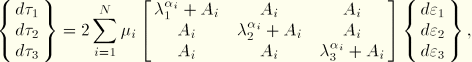
For the simple shear case the principal stretches ![]() and
and ![]() are computed from the shear strain
are computed from the shear strain ![]() (as given in an earlier expression). Thus, the same form of equations is used in checking material stability during simple shear deformation.
(as given in an earlier expression). Thus, the same form of equations is used in checking material stability during simple shear deformation.
For material stability (i.e., for ![]() to be positive definite) the following conditions must be satisfied:
to be positive definite) the following conditions must be satisfied:
![]()
![]()
![]()