The lower-order quadrilateral continuum elements in ABAQUS/Standard of type CPS4I, CPE4I, CAX4I, CPEG4I, and C3D8I as well as the related hybrid, coupled temperature-displacement and pore pressure elements are enhanced by incompatible modes to improve the bending behavior. In addition to the displacement degrees of freedom, incompatible deformation modes are added internal to the elements. The primary effect of these degrees of freedom is to eliminate the so-called parasitic shear stresses that are observed in regular displacement elements if they are loaded in bending.

In addition, these degrees of freedom eliminate artificial stiffening due to Poisson's effect in bending. In regular displacement elements the linear variation of the axial stress due to bending is accompanied by a linear variation of the stress perpendicular to the bending direction, which leads to incorrect stresses and an overestimation of the stiffness. The incompatible modes prevent such a stress from occurring.

In the nonhybrid elements (except CPS4I) additional incompatible modes are added to prevent locking of the elements for approximately incompressible material behavior. For fully incompressible material behavior, hybrid elements must be used. In these elements pressure degrees of freedom are added to enforce a linear pressure variation inside the element. In the hybrid elements the additional incompatible modes used to prevent locking are not included.

The incompatible mode elements perform almost as well as second-order elements in many situations if the elements have an approximately rectangular shape. The performance is considerably less if the elements have a parallelogram shape. For trapezoidal element shapes the performance is not much better than the performance of regular displacement elements.

Because of the internal degrees of freedom (4 for CPS4I; 5 for CPE4I, CAX4I, and CPEG4I; and 13 for C3D8I) the elements are somewhat more expensive than regular displacement elements. However, the additional degrees of freedom do not substantially increase the wavefront size since they can be eliminated immediately. In addition, it is not necessary to use selectively reduced integration, which partially offsets the cost of the additional degrees of freedom.

The geometrically linear incompatible mode formulation used in ABAQUS is related to the work presented by Simo and Rifai (1990). Simo's formulation is very similar to much earlier work done by Wilson et al. (1973) and Taylor et al. (1976). The nonlinear formulation is based on work by Simo and Armero (1992).

Geometrically linear formulation

As discussed in the paper by Simo, the incompatible mode formulation can be derived in a rigorous way from the general Hu-Washizu variational principle. In this discussion we will not present this derivation but use only the key results of Simo's work.

In the incompatible mode formulation, the displacement gradient is augmented with an additional, incompatible displacement gradient field :

The incompatible displacement gradient is chosen internal to an element. The field cannot be selected arbitrarily. It must be independent of the regular displacement gradient.

which can also be expressed in the form

In addition, it must be orthogonal to any constant gradient field, which yields the condition

If these conditions are violated, the element does not pass the patch test.

The last condition is used to obtain a suitable general form of the incompatible modes. We describe the incompatible field as a transformation of a parametric gradient field :

where is the parametric transformation at the center of the element

is the Jacobian of the parametric transformation at the location , and is the Jacobian at the center of the element. For planar elements the Jacobian can be written as

where is the thickness; for axisymmetric elements it is

where is the radius; and for three-dimensional elements it is

Substitution of Equation 3.2.5–2 in Equation 3.2.5–1 allows us to create a simple condition for :

For two-dimensional elements this yields

and for three-dimensional elements,

This makes it possible to write as a simple polynomial in . The principal contribution to can be written in the form

where are vectorial degrees of freedom and are vectors and the summation extends over the parametric coordinates. In two-dimensional elements and are vectors of the form

and in three-dimensional elements

The principal contribution to the incompatible displacement gradient hence becomes

With the addition of these terms, parasitic shear and Poisson's effect in bending are eliminated. Note that the vectors in appear in a similar form as the nodal displacement vectors in ,

and can be treated similar to displacement degrees of freedom.

For approximately incompressible material behavior, bilinear patterns in the hydrostatic stress can still be observed in all elements except CPS4I. These patterns can be eliminated by the introduction of additional incompatible modes of the form

where are additional scalar degrees of freedom. For two-dimensional elements a single term is added with

In the three-dimensional elements four additional terms are added with

Thus, the incompatible displacement gradient takes the final form

The symmetric part of the incompatible displacement gradient contributes to incompatible strains:

The skew-symmetric part plays no role in the geometrically linear formulation.

Geometrically nonlinear formulation

Since we want to use a formulation that can be used for any material model, we want to express the incompatible modes as a modification of the deformation gradient . The most obvious approach is to add the incompatible modes to the deformation gradient:

This approach has been used successfully by Simo and Armero. Elements formulated on this basis satisfy the large-strain patch test; i.e., any patch of elements will be able to represent homogeneous deformations exactly. However, once the elements become distorted due to deformation, the patch test will no longer be satisfied in an incremental sense; that is, subsequent homogeneous deformations will not be represented exactly. This turns out to be a fatal flaw in the formulation for problems involving large distortions in compression.

Satisfaction of the instantaneous patch test requires the addition of an incompatible deformation rate tensor to the standard rate of deformation:

To obtain an approximate relation of this type, we write the total deformation gradient as the product of a series of incremental deformation gradients:

Principal incompatible modes are then added to the incremental deformation gradient:

Similar to Equation 3.2.5–2 the principal incompatible modes are described as a transformation of the parametric gradient field :

where is the parametric transformation at the center of the element in the state at the start of the increment,

is the Jacobian of the parametric transformation at the location ; and is the Jacobian at the centroid at the start of the increment. Note that is evaluated based on the deformation caused by the displacement degrees of freedom only and does not include the volume change due to the incompatible modes.

The incremental parametric gradient field has exactly the same form as in the linear formulation,

which yields the principal incremental incompatible deformation gradient

Bilinear volumetric terms are added to the principal terms in a multiplicative way:

The variation in the gradient of the position with respect to the current state is obtained from the fundamental relation

with

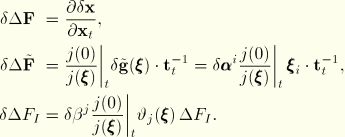
This allows us to write for

The integral of the principal incompatible modes over the element volume at the start of the increment is, hence, equal to

Note that the integral will vanish if the incremental deformation is homogeneous; that is, , since in that case the integral can be written as

Hence, the incremental patch test will be satisfied. The rate of the gradient of the position with respect to the current state is obtained similar to the variation

with

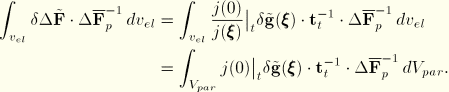
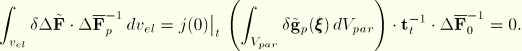
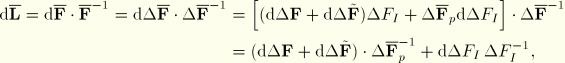
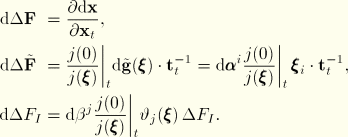
For a finite-strain increment we use the midincrement approach proposed by Hughes and Winget. This yields

The second variation is obtained in the usual way. Since the regular deformation gradient and the principal incompatible modes are purely displacement based, the initial stress stiffness terms are readily obtained as

where is the gradient of the velocity and is the gradient of the displacement variation including the primary incompatible modes. Further, is the rate of deformation, and is the variation in the deformation.

The additional bilinear modes appear in the first variation only as variations (the values themselves do not appear); hence, the contributions to the second variation can be neglected.