
The first step in defining contact between two structures in ABAQUS is to create surfaces using the *SURFACE option. Next, pairs of surfaces that may contact each other are created using the *CONTACT PAIR option. Each contact pair refers to a surface interaction definition, which is created with the *SURFACE INTERACTION option. A contact pressure-clearance relationship and friction properties can be assigned to a surface interaction definition.

Surfaces are created with the *SURFACE option by identifying all of the element faces that form the surface. This is done in much the same way as defining distributed pressure loads.
Surfaces on continuum elements
A two-dimensional, first-order continuum element, such as CPE4, has four faces consisting of the segments defined by nodes 1–2, 2–3, 3–4, and 4–1, respectively, as shown in Figure 11–3. The face identifiers consist of the letter “S” followed by the face number. For example, use the following option block to include face 2 of the element shown in Figure 11–3 in a surface called FLANGE1:
*SURFACE, NAME=FLANGE1 5, S2
As is the case for many options in ABAQUS, both element numbers and element sets can be used; the use of element sets can make the definition of large surfaces much easier. It is valid to specify both element sets and individual elements in the same *SURFACE option block, as shown in Figure 11–4 and the example below. The surface TOPSURF consists of the element faces shown in Figure 11–4 and is created as follows:
*ELSET, ELSET=TOP, GENERATE 5, 8 *SURFACE, NAME=TOPSURF TOP, S3 5, S4 8, S2
ABAQUS can determine the free faces of two- and three-dimensional continuum elements automatically and use them to create a surface. To use this capability, simply include all the elements whose free faces make up the surface on the data lines of the *SURFACE option. Either element sets or individual element numbers can be used. If elements in the interior of the body are included, ABAQUS will ignore them. For example, the surface shown in Figure 11–4 could also be defined using
*SURFACE, NAME=TOPSURF TOP,
Surfaces on shell, membrane, and rigid elements
For shell, membrane, and rigid elements you must specify which side of the element forms the contact surface. The side in the direction of the positive element normal is called SPOS, while the side in the direction of the negative element normal is called SNEG, as shown in Figure 11–5. As discussed in Chapter 5, “Using Shell Elements,” the connectivity of an element defines the positive element normal. The positive element normals can be viewed in ABAQUS/Viewer.
The following option block defines surface SURF1 as the surface composed of all the SPOS faces of the elements in element set SHELLS:
*SURFACE, NAME=SURF1 SHELLS, SPOS
Restrictions on the types of surfaces that can be created in ABAQUS are discussed in “Defining surfaces,” Section 2.3 of the ABAQUS Analysis User's Manual; please read them before beginning a contact simulation.
Rigid surfaces
Rigid surfaces are the surfaces of rigid bodies. They can be defined as an analytical shape, or they can be based on the underlying surfaces of elements associated with the rigid body.
Analytical rigid surfaces are created by defining a series of connected lines, arcs, and parabolas. The parameter ANALYTICAL SURFACE on the *RIGID BODY option binds an analytical rigid surface (defined with the TYPE parameter on the *SURFACE option) with a rigid body. The *RIGID BODY option must be defined in the model definition. The TYPE parameter on the *SURFACE option defines the dimensionality of the surface, and it has three possible values:
Use TYPE=SEGMENTS to define a two-dimensional analytical rigid surface.
Use TYPE=CYLINDRICAL to define a three-dimensional analytical rigid surface that is extruded infinitely in the out-of-plane direction.
Use TYPE=REVOLUTION to define a three-dimensional analytical rigid surface of revolution.
The following is an example input for the two-dimensional analytical rigid surface named SRIGID shown in Figure 11–6:
*SURFACE, TYPE=SEGMENTS, NAME=SRIGID START, 5.0, 0.0 LINE, 10.0, 0.0 CIRCL, 15.0, 5.0, 10.0, 5.0where the rigid body is defined by
*RIGID BODY, ANALYTICAL SURFACE=SRIGID, REF NODE=10000
Discretized rigid surfaces are based on the underlying elements that make up a rigid body; thus, they can be more geometrically complex than analytical rigid surfaces. Discretized rigid surfaces are defined using the *SURFACE option in exactly the same manner as surfaces on deformable bodies.

Define possible contact between two surfaces in an ABAQUS simulation by giving the surface names on the *CONTACT PAIR option. When you define a contact pair, you must decide whether the magnitude of the relative sliding will be small or finite. The default is the more general finite-sliding formulation. The small-sliding formulation is appropriate if the relative motion of the two surfaces is less than a small proportion of the characteristic length of an element face. The small-sliding formulation is selected by including the SMALL SLIDING parameter on the *CONTACT PAIR option. Using the small-sliding formulation will result in a more efficient analysis.
Each contact pair must refer to a surface interaction definition, in much the same way that each element must refer to an element property definition. Use the INTERACTION parameter on the *CONTACT PAIR option to refer to a *SURFACE INTERACTION option where the different surface interaction models, such as *FRICTION, can be defined.
The following example:
*CONTACT PAIR, INTERACTION=FRIC, SMALL SLIDING FLANGE1, FLANGE2 *SURFACE INTERACTION, NAME=FRIC *FRICTION 0.1,specifies that surfaces FLANGE1 and FLANGE2 might interact with each other and that the amount of relative sliding that occurs will be considered to be small. The interaction between the surfaces includes friction, with a coefficient of friction of 0.1.

ABAQUS uses a pure master-slave contact algorithm: nodes on one surface (the slave) cannot penetrate the segments that make up the other surface (the master), as shown in Figure 11–7.
The algorithm places no restrictions on the master surface; it can penetrate the slave surface between slave nodes, as shown in Figure 11–7. The order of the two surfaces given on the *CONTACT PAIR option is important because it determines which surface is the master surface and which is the slave surface. The first surface is taken to be the slave surface, and the second is the master surface.A consequence of this strict master-slave formulation is that you must be careful to select the slave and master surfaces correctly to achieve the best possible contact simulation. Some simple rules to follow are:
the slave surface should be the more finely meshed surface; and
if the mesh densities are similar, the slave surface should be the surface with the softer underlying material.

When using the small-sliding formulation, ABAQUS establishes the relationship between the slave nodes and the master surface at the beginning of the simulation. ABAQUS determines which segment on the master surface will interact with each node on the slave surface. It maintains these relationships throughout the analysis, never changing which master surface segments interact with which slave nodes. If geometric nonlinearity is included in the model by using the NLGEOM parameter on the *STEP option, the small-sliding algorithm accounts for any rotation and deformation of the master surface and updates the load path through which the contact forces are transmitted. If geometric nonlinearity is not included in the model, any rotation or deformation of the master surface is ignored and the load path remains fixed.
The finite-sliding contact formulation requires that ABAQUS constantly determine which part of the master surface is in contact with each slave node. This is a very complex calculation, especially if both the contacting bodies are deformable. The structures in such simulations can be either two- or three-dimensional. ABAQUS can also model the finite-sliding self-contact of a deformable body. Such a situation occurs when a structure folds over onto itself. This capability is available only for two-dimensional (plane strain, plane stress, and axisymmetric) problems.
The finite-sliding formulation for contact between a deformable body and a rigid surface is not as complex as the finite-sliding formulation for two deformable bodies. Finite-sliding simulations where the master surface is rigid can be performed for both two- and three-dimensional models.

When selecting elements for contact analyses, it is better, in general, to use first-order elements for those parts of a model that will form a slave surface. Second-order elements can cause problems in contact simulations because of the way these elements calculate consistent nodal loads for a constant pressure. The consistent nodal loads for a constant pressure, ![]() , on a second-order, two-dimensional element with area
, on a second-order, two-dimensional element with area ![]() are shown in Figure 11–8.
are shown in Figure 11–8.
Figure 11–8 Equivalent nodal loads for a constant pressure on a two-dimensional, second-order element.
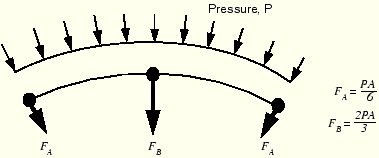
The contact algorithms base important decisions on the forces acting on the slave nodes. It is difficult for the algorithms to tell if the force distribution shown in Figure 11–8 represents a constant contact pressure or an actual variation across the element. The equivalent nodal forces for a three-dimensional, second-order brick element are even more confusing because they do not even have the same sign for a constant pressure, making it very difficult for the contact algorithm to work correctly, especially for nonuniform contact. Therefore, to avoid such problems, ABAQUS automatically adds a midface node to any face of a second-order, three-dimensional brick or wedge element that defines a slave surface. The equivalent nodal forces for a second-order element face with a midface node have the same sign for a constant pressure, although they still differ considerably in magnitude.
The equivalent nodal forces for applied pressures on first-order elements always have a consistent sign and magnitude; therefore, there is no ambiguity about the contact state that a given distribution of nodal forces represents.
If your geometry is complicated and requires the use of an automatic mesh generator, the modified second-order tetrahedral elements (C3D10M) in ABAQUS should be used. These elements are designed to be used in complex contact simulations; regular second-order tetrahedral elements (C3D10) have zero contact force at their corner nodes, leading to poor predictions of the contact pressures. They should, therefore, not be used in contact problems. The modified second-order tetrahedral elements can calculate the contact pressures accurately.