Recursive Algorithms: Square Root

Suppose Java did not provide a square root procedure. Could we build one ourselves?

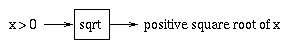
The mathematical definition of the problem is:

Given x>0, find y such that y²=x.

This tells us what we want but not how to get it. We need an algorithm.

Think back to what you did when you first learned to find square roots. Recall that if y is the square root of x, then y²=x, so x/y=y. This gives us an idea for an algorithm:

Guess some value g for y and test it.
Compute x / g.
If x / g is close enough to g, return g. Otherwise, try a better guess.

This suggests that we need the following procedures:

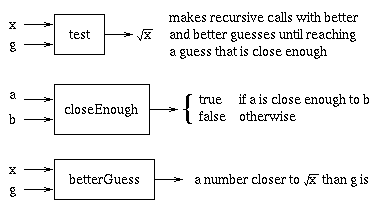
Then, to solve the square root problem, we can reduce it to test:


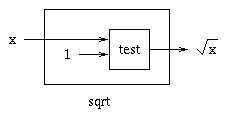
double sqrt(double x) {

   return test(x, 1);

}

Note: We have defined sqrt in terms of test, but we have not yet defined test. We just have its specification, and have deferred its implementation. In other words, we have treated it as a black box to be filled in later.

Doing top down refinement -- decomposing a problem into smaller problems that can be filled in later -- is helpful in the algorithm design and implementation process because it saves you from thinking about all the details at once. test: If x / g is close to g, return g, return g. Otherwise, try a better guess.


double test(double x, double g) {

   if closeEnough(x/g, g)

      return g;

   else

      return test(x, betterGuess(x, g));

}

We haven't even really thought about closeEnough or betterGuess yet. Now it's time to fill those in.

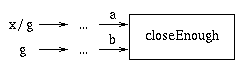
closeEnough: returns true iff a is "close" to b.

This is a vague specification. Let's define "close" to mean within .001 of each other.


boolean closeEnough(double a, double x) {

   return (Math.abs(a - b) < .001);

}

betterGuess: returns a value closer to the square root of x than g is.

If x / g is not close enough to g, how can we bring them closer? We can choose a new guess that is the average of x / g and g.


double betterGuess(double x, double g) {

   return ((g + x/g) / 2);

}

Now we have the whole implementation. We reduced sqrt to test, and then filled in closeEnough and betterGuess. Let's try an example:

`sqrt(2)`	Guess `g`	`x` / `g`	New guess, (`g` + `x` / `g`) / 2
`test(2, 1)`	1	2 / 1 = 2	(2+1)/2 = 1.5
`test(2, 1.5)`	1.5	2 / 1.5 = 1.3333	(1.3333+1.5)/2 = 1.4167
`test(2, 1.4167)`	1.4167	2 / 1.4167 = 1.4118	(1.4167+1.4118)/2 = 1.4142
`test(2, 1.4142)`	1.4142	...

We could print the guess each time test is called to see how it converges.

To summarize, some advantages of black box abstraction and top down refinement in algorithm design and implementation include:

hides details (a property of abstraction in general)
allows us to express the general framework while postponing details for later
gives us building blocks we might reuse in other situations
lets us use local names
lets us replace parts of the implementation to improve it.
For example, suppose we try sqrt(.000001). If our solution is only within .001 of the square root, .001, this is close to useless. Maybe we can be more clever about closeEnough. Suppose we modify closeEnough(a, b) to return true iff a and b differ by a small percentage. (Note that this also helps us stop earlier on large square roots.)
```
boolean closeEnough(double a, double b) {

   return (Math.abs(a - b) < (b * 0.001));   // a is within 0.1% of b

}

          
```
We just replace the definition of closeEnough. We don't have to change any of the other procedures.

Newton-Raphson Root Finding Algorithm

The discussion of finding square roots seems academic in some sense because there's already a builtin Math.sqrt method. But what if we want to take cube roots or fourth roots? Let's develop an algorithm.

We want, for some n, to have a box

In other words, we want to find x such that xⁿ = w. Rewriting, xⁿ - w = 0.

Therefore, if f(x) = xⁿ - w, we want to find the value of x where f(x) = 0, that is, where the curve crosses the x-axis.

So the question becomes more general: For a given function f(x), how do we find the place where the curve crosses zero? We could solve this by guessing values as before and trying better guesses until we reach the solution. But which guesses do we try in order to reach the solution quickly?

To simplify the problem, let's assume that f(x) over the interval of interest

crosses zero in exactly one place,
is differentiable (i.e., we can take the derivative),
the derivative on the interval is always negative or always positive.

Given these facts, what might we do?

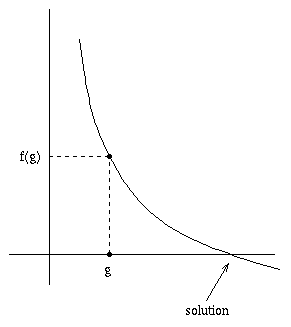
Let's suppose we start by guessing g. If we could somehow use the general "direction" of the curve to guide us, it could lead us to a better guess.

The derivative provides us with exactly that. The derivative f'(g) gives us the slope of the curve at g, so we can find a new guess closer to the solution by determining where the line passing through f(g) with slope f'(g) crosses the x-axis.

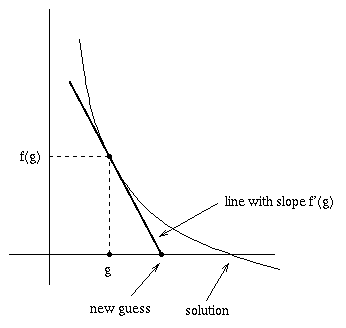
Then we do it again:

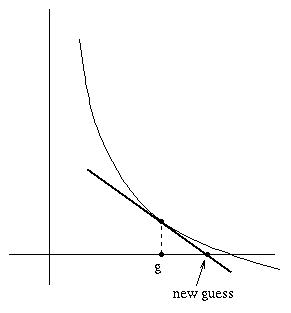
until we get close enough to the final solution. This is known as Newton's method.

So two details remain:

Given the slope of the line, how do we compute the new guess?
How do we know when we're close enough to the final solution?

Finding the New Guess

Let's consider the new guess first. We have:

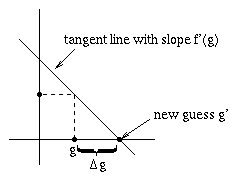
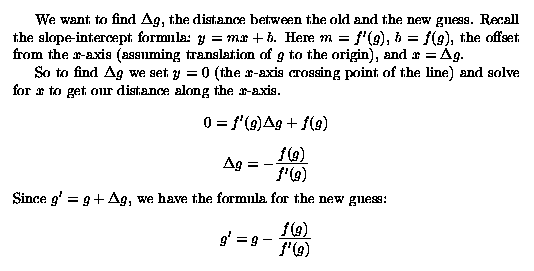
Determining When We're Close Enough

We can do the same thing we did for the square root algorithm -- see if the old and new guesses are within a small percentage of each other.

Putting it All Together

Let's build a RootFinder class whose constructor takes a single parameter n and creates an object that can be used to find nth roots. What methods will be needed inside the RootFinder?

Public methods:

We'll want a public method root that takes in a double w and returns the nth root of w.

Private methods:

findRoot(w, g) -- finds the nth root of w, starting from guess g.
f(w, g) -- evaluates f(g) = gⁿ - w.
fPrime(w, g) -- evaluates f'(g) = ng^n-1.
closeEnough(a, b) -- returns true iff a is "close" to b.

Now let's write the code:


import cs101.terminal.*;



public class RootFinder {

    int n;

    RootFinder(int n) {

        this.n = n;

    }



    double f(double w, double g) {

        return (Math.pow(g,n) - w);

    }



    double fPrime(double g) {

        return (n * Math.pow(g, n-1));

    }



    boolean closeEnough(double a, double b) {

        return (Math.abs(a-b) < Math.abs(b * 0.0001));

    }



    double findRoot(double w, double g) {

        Terminal.println("  guessing " + g);

        double newGuess = g - f(w,g) / fPrime(g);

        if (closeEnough(newGuess, g))

            return newGuess;

        else

            return findRoot(w, newGuess);

    }



    public double root(double w) {

        return findRoot(w,1);

    }

}

Kenneth J. Goldman

Last modified: Wed Feb 19 23:49:59 CST