Assume the ALU in the processor is capable of floating point arithmetic. If you need a constant in your code, such as -1.0, you may assume the constant is in data memory or the register file as long as your code doesn't overwrite it. You must add your terms to the variables you're using for cos(X) and sin(X). List the variables you need in your code and their location in memory or register file.
cos(X) = 1 - X^2/2! + X^4/4! - X^6/6! + X^8/8! - ...
sin(X) = X - X^3/3! + X^5/5! - X^7/7! + X^9/9! - ...
| Instruction mnemonic | Description |
|---|---|
| Mov Ra, d | RF[a] = D[d] |
| Mov d, Ra | D[d] = RF[a] |
| Add Ra, Rb, Rc | RF[a] = RF[b] + RF[c] |
| Sub Ra, Rb, Rc | RF[a] = RF[b] - RF[c] |
| Mult Ra, Rb, Rc | RF[a] = RF[b] * RF[c] |
| Div Ra, Rb, Rc | RF[a] = RF[b] / RF[c] |
// Location Description
// R[0] COSX -- A running total of cos(X) terms
// R[1] SINX -- A running total of sin(X) terms
// R[2] NEGATIVEONE -- Constant -1
// R[3] FACTORIAL -- A running factorial
// R[4] ONE -- Constant 1
// R[5] FACTORIALCOUNT -- A running count of factorials
// R[6] POWERX -- A running power of X
// R[7] X -- A constant angle X in radians
// R[8] TERM -- A temporary calculation
// Setup term equation
Mult R6, R6, R2 // POWERX = POWERX * NEGATIVEONE
Mult R6, R6, R7 // POWERX = POWERX * X
Add R5, R5, R4 // FACTORIALCOUNT = FACTORIALCOUNT + ONE
Mult R3, R3, R5 // FACTORIAL = FACTORIAL * FACTORIALCOUNT
// Calculate term
Div R8, R6, R3 // TERM = POWERX / FACTORIAL
// Add term to running cos(x)
Add R0, R0, R8 // COSX = COSX + TERM
// Setup next term equation
Mult R6, R6, R7 // POWERX = POWERX * X
Add R5, R5, R4 // FACTORIALCOUNT = FACTORIALCOUNT + ONE
Mult R3, R3, R5 // FACTORIAL = FACTORIAL * FACTORIALCOUNT
// Calculate term
Div R8, R6, R3 // TERM = POWERX / FACTORIAL
// Add term to running sin(x)
Add R1, R1, R8 // SINX = SINX + TERM
The number of instructions is 2^20 = 1048576 instructions.
(a). Invalid. The path from memory data out must go through a register in the register file. This blocks a one-cycle transfer.
(b). Invalid. Only one register from the register file may be written per cycle.
(c). Invalid. The ALU only operates on registers from the register file. The result is only written to the register file.
R[0] = D[4]
R[1] = D[5]
R[2] = D[7]
R[0] = R[0] + R[1]
R[0] = R[0] - R[2]
D[8] = R[0]
2^4 = 16 instructions.
D[20] = D[30] + D[20] + D[18]
T0 Fetch instruction 1
T1 Decode instruction 1
T2 Data memory location 1 is transferred to register 0 in register
file
T3 Fetch instruction 2
T4 Decode instruction 2
T5 Data memory location 9 is transferred to register 1 in register
file
T6 Fetch instruction 3
T7 Decode instruction 3
T8 Register 0 and register 1 are added together. The result is
transferred to register 0
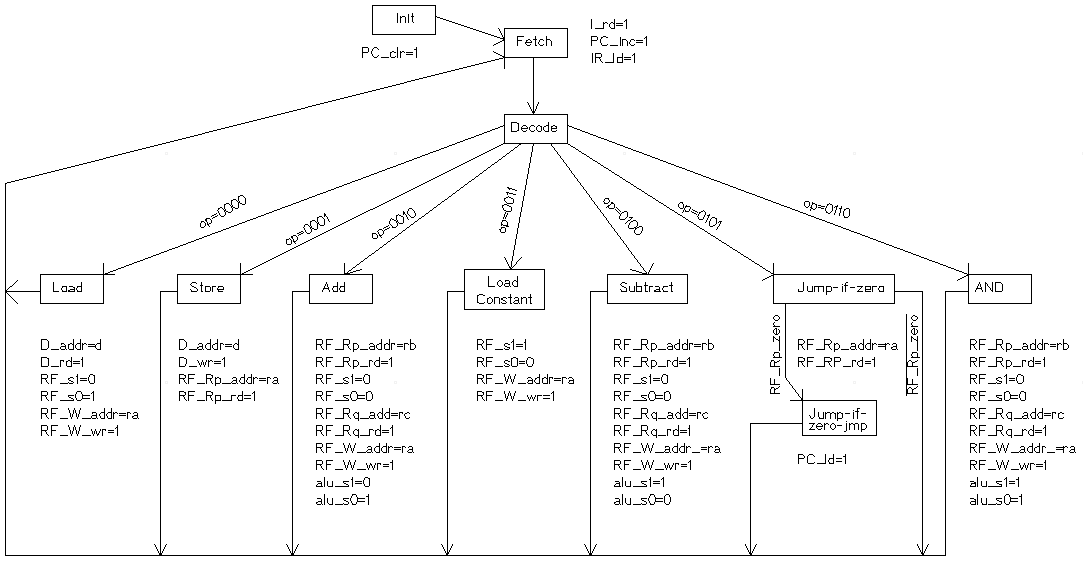
The ALU must support the bitwise AND operation. The select lines s1=1 and s0=1 selects the bitwise AND circuit. Otherwise, the block diagram in figure 8.12 is unchanged.
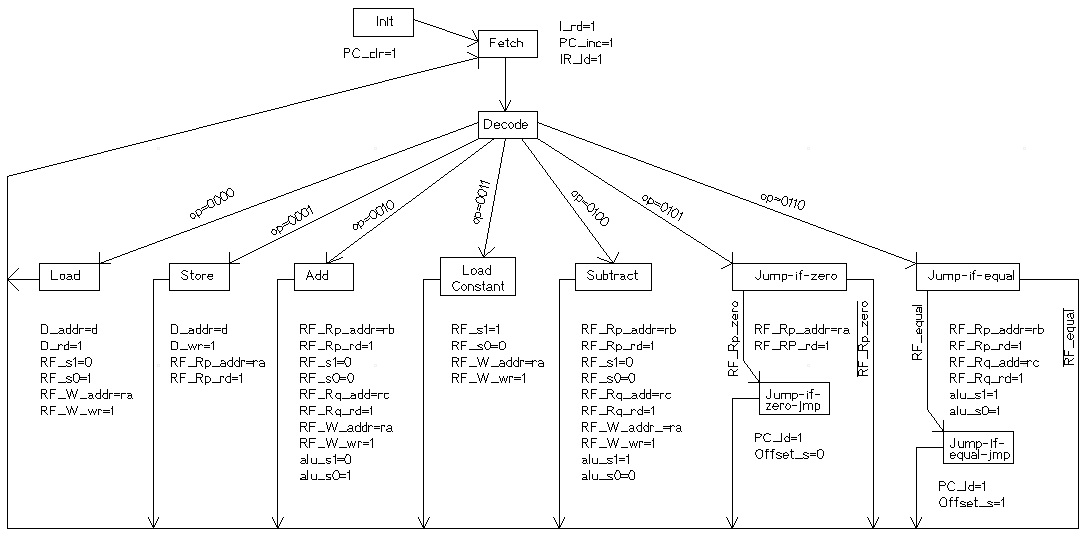
The ALU must support comparing 2 operands. The select lines s1=1 and s0=1 selects the comparison circuit. The output of the comparison is a status bit called RF_equal. Figure 8.12 is modified by putting a multiplexer between the IR register and the adder circuit next to the PC register. When the signal Offset_s is 0, the multiplexer passes the IR bits 7 down to 0 sign extended. When the signal Offset_s is 1, the multiplexer passes IR bits 11 down to 8 sign extended.
// Data memory
// D[9] holds N
// Registers
// R[0] holds 0
// R[1] holds 1
// R[2] holds i
// R[3] holds sum
// R[4] holds N
// R[5] holds i - N result
MOV R0, #0 // Load constant 0
MOV R1, #1 // Load constant 1
MOV R2, #1 // Initialize i
MOV R3, #0 // Initialize sum
MOV R4, 9 // Load D[9] aka N
Loop: SUB R5, R2, R4 // subtract i from N
JMPZ R5, Finished // jump to finished if (N - i) is 0
ADD R3, R3, R2 // Add i to sum
ADD R2, R2, R1 // Increment i
JMPZ R0, Loop // Repeat loop
Finished:
// This solution uses the AND instruction
MOV R0, 240
MOV R1, 241
MOV R2, 242
MOV R3, 243
MOV R4, 244
MOV R5, 245
MOV R6, 246
MOV R7, 247
AND R0, R0, R1
AND R2, R2, R3
AND R4, R4, R5
AND R6, R6, R7
AND R0, R0, R2
AND R4, R4, R6
AND R0, R0, R4
JMPZ R0, Finish
MOV R0, #0 // Load constant 0
MOV 252, R0
Finish:
// This solution just uses the existing 6 instructions. No
// need for an AND instruction
MOV R0, 240
JMPZ R0, Finish
MOV R0, 241
JMPZ R0, Finish
MOV R0, 242
JMPZ R0, Finish
MOV R0, 243
JMPZ R0, Finish
MOV R0, 244
JMPZ R0, Finish
MOV R0, 245
JMPZ R0, Finish
MOV R0, 246
JMPZ R0, Finish
MOV R0, 247
JMPZ R0, Finish
MOV R0, #0 // Load constant 0
MOV 252, R0
Finish: