- A. X = (a + b)(c + d) given a = 1, b = 1, c = 0, d = 0
0. - B. Y = a + b * c + d given a = 0, b = 1, c = 0, d = 0
0. - C. Z = a * b * c * d' + a' * b * c * d' + a' * b' * c * d given a = 0, b = 1, c = 1, d = 0
1.
- A. X = AB + A'B'

- B. Y = a + (b + (c + d))
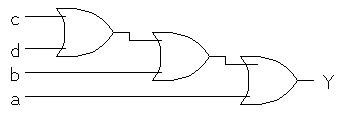
- C. Z = abc' + a'bc + a'b'c

- D. W = mn + m'no + p

- A. X + X * Y = X
X * (1 + Y)
X * 1
X - B. X * (X + Y) = X
X * X + X * Y
X + X * Y
X * (1 + Y)
X * 1
X - C. X * Y + X * Y' = X
X * (Y + Y')
X * 1
X - D. (X + Y) * (X + Y') = X
X + (Y * Y')
X + 0
X - E. X * Y + X' * Z + Y * Z = X * Y + X' * Z
X * Y + X' * Z + Y * Z * 1
X * Y + X' * Z + Y * Z * (X + X')
X * Y + X' * Z + X * Y * Z + X' * Y * Z
X * Y + X * Y * Z + X' * Z + X' * Y * Z
X * Y * (1 + Z) + X' * Z * (1 + Z)
X * Y * 1 + X' * Z * 1
X * Y + X' + Z - F. (X + Y) * (X' + Z) * (Y + Z) = (X + Y) * (X' + Z)
(X + Y) * (X' + Z) * ((Y + Z) + 0)
(X + Y) * (X' + Z) * ((Y + Z) + (X * X'))
(X + Y) * (X' + Z) * (X + Y + Z) * (X' + Y + Z)
(X + Y) * (X + Y + Z) * (X' + Z) * (X' + Z + Y)
(X + Y) * (1 + Z) * (X' + Z) * (1 + Y)
(X + Y) * 1 * (X' + Z) * 1
(X + Y) * (X' + Z)
- A. pump = water * enabled
- B. alarm = light * night * motion'
- C. open = enabled * (rain + freeze)'
- A.

- B.
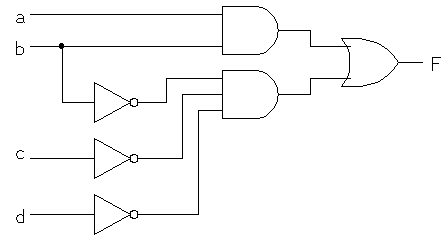
- C.

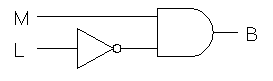
B = M * L'
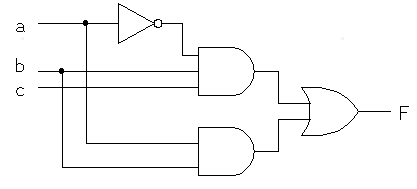
F = a(b + c)(d') + ac'(b + d)
F = ad'(b + c) + ac'(b + d)
F = ad'b + ad'c + ac'b + ac'd
F = abd' + acd' + abc' + ac'd
F = a'b(c + d') + a(b' + c) + a(b + d)c
F = a'b(c + d') + a(b' + c) + ac(b + d)
F = a'bc + a'bd' + ab' + ac + acb + acd
F = a'bc + a'bd' + ab' + ac + abc + acd
F = abc + a'b
F' = (abc + a'b)'
F' = (abc)'(a'b)'
F' = (a' + b' + c')(a + b')
F' = a(a' + b' + c') + b'(a' + b' + c')
F' = aa' + ab' + ac' + a'b' + b'b' + b'c'
F' = 0 + ab' + ac' + a'b' + b' + b'c'
F' = ab' + ac' + a'b' + b' + b'c'
F' = ab' + a'b' + b' + b'c' + ac'
F' = b'(a + a' + 1 + b') + ac'
F' = b'1 + ac'
F' = b' + ac'
F = ac' + abd' + acd
F' = (ac' + abd' + acd)'
F' = (ac')'(abd')'(acd)'
F' = (a' + c)(a' + b' + d)(a' + c' + d')
F' = (a'(a' + b' + d) + c(a' + b' + d))(a' + c' + d')
F' = (a' + a'b' + a'd + a'c + b'c + cd)(a' + c' + d')
F' = (a'(1 + b' + d + c) + b'c + cd)(a' + c' + d')
F' = (a' + b'c + cd)(a' + c' + d')
F' = a'(a' + c' + d') + b'c(a' + c' + d') + cd(a' + c' + d')
F' = a'a' + a'c' + a'd' + a'b'c + b'cc' + b'cd' + a'cd + cc'd + cdd'
F' = a' + a'c' + a'd' + a'b'c + b'cc' + b'cd' + a'cd + cc'd + cdd'
F' = a' + a'c' + a'd' + a'b'c + b'0 + b'cd' + a'cd + 0d + c0
F' = a' + a'c' + a'd' + a'b'c + b'cd' + a'cd
F' = a' + a'c' + a'd' + a'b'c + a'cd + b'cd'
F' = a'(1 + c' + d' + b'c + cd) + b'cd'
F' = a'1 + b'cd'
F' = a' + b'cd'
- A.
- B.
- C.

- D.
- A.
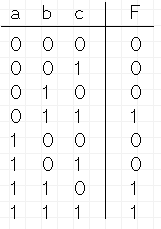
- B.
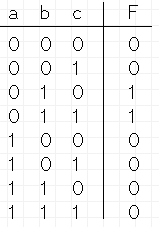
- C.
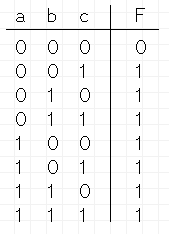
- D.

- A. a'bc + abc + abc'
- B. a'bc + a'bc'
- C. a'b'c + a'bc' + a'bc + ab'c' + ab'c + abc' + abc
- D. a'b'c' + a'bc' + ab'c' + abc'
- A. (a + b)' * a
(a' * b') * a
a * a' * b'
0 * b'
0
0 is not equal to a + b'. - B.
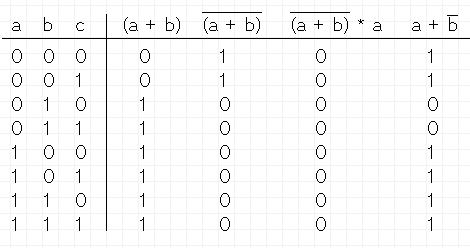
((a + b)' * a) is not equal to (a + b')
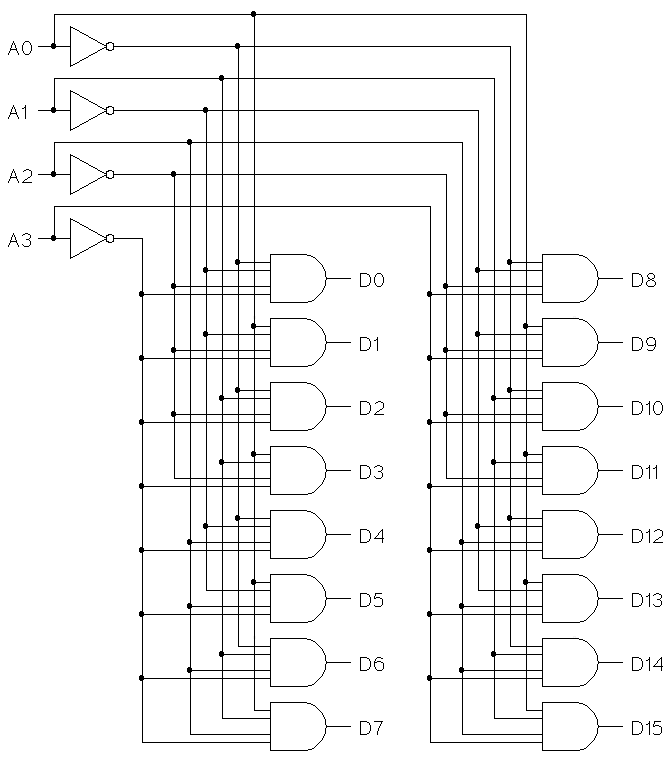
- A. First circuit is (ab + cd)
Manipulating the equation into minterms and minterm order.
abc + abc' + acd + a'cd
abcd' + abcd + abc'd' + abc'd + ab'cd + abcd + a'b'cd + a'bcd
abcd' + abcd + abc'd' + abc'd + ab'cd + a'b'cd + a'bcd
a'b'cd + a'bcd + ab'cd + abc'd' + abc'd + abcd' + abcd
Second circuit is ((ab)'(cd)')''
Manipulating the equation into minterms and minterm order.
(ab)'(cd)'
(a' + b')(c' + d')
a'(c' + d') + b'(c' + d')
a'c' + a'd' + b'c' + b'd'
a'b'c' + a'bc' + a'b'd' + a'bd' + a'b'c' + ab'c' + a'b'd' + ab'd'
a'b'c' + a'bc' + a'b'd' + a'bd' + ab'c' + ab'd'
a'b'c'd' + a'b'c'd + a'bc'd' + a'bc'd + a'b'c'd' + a'b'cd' + a'bc'd' + a'bcd' + ab'c'd' + ab'c'd + ab'cd'
a'b'c'd' + a'b'c'd + a'bc'd' + a'bc'd + a'b'cd' + a'bcd' + ab'c'd' + ab'c'd + ab'cd'
a'b'c'd' + a'b'c'd + a'b'cd' + a'bc'd' + a'bc'd + a'bcd' + ab'c'd' + ab'c'd + ab'cd'
Since the minterms are not equal the two circuits are not equivalent. - B.
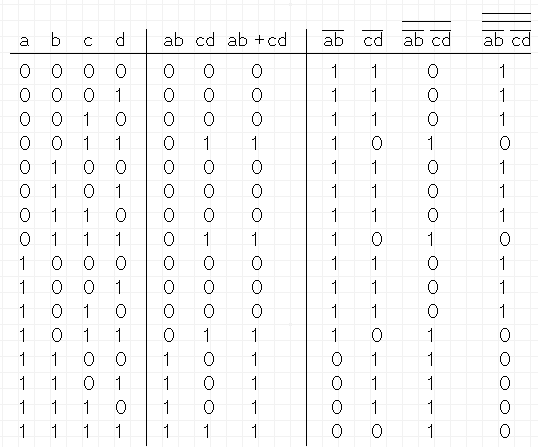
The two circuits are not equal.
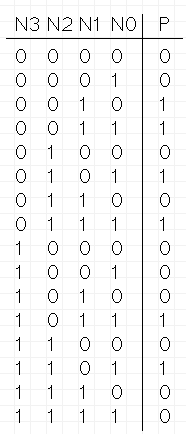
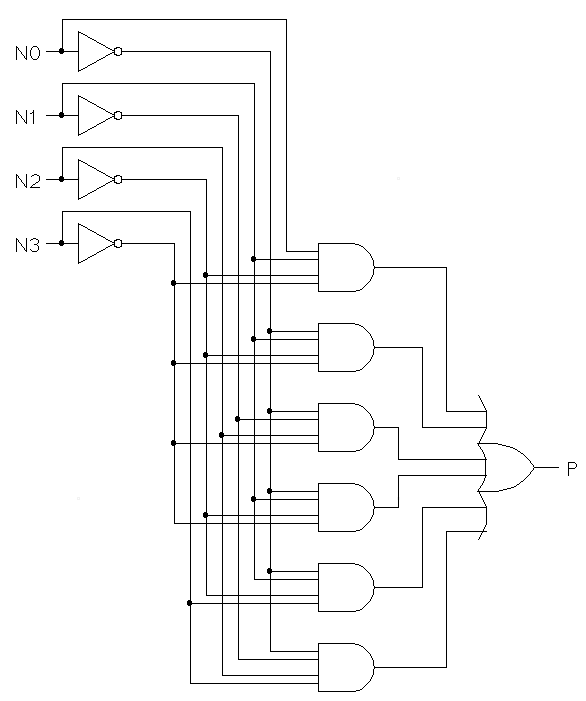
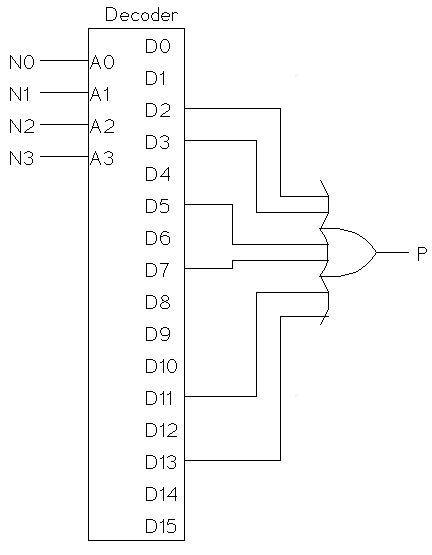
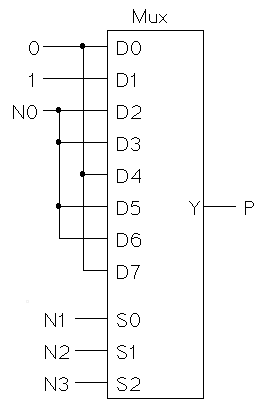
P = m2 + m3 + m5 + m7 + m11 + m13