Difference between revisions of "Binary Search Tree Assignment"

From CSE425S Wiki
Jump to navigation Jump to search
 
(60 intermediate revisions by the same user not shown)
Line 1: Line 1:
−
We will implement a binary search tree data structure as well as a few Higher Order Function Hall of Fame inductees.
+
We will implement a binary search tree data structure as well as Higher Order Function Hall of Fame inductees: find and fold.
  
 
=Background=
 
=Background=
 +
==student record example==
 +
<youtube>dxqoq8R3k34</youtube>
 +
 +
<nowiki>type course = (string*int)
 +
type student = {first_name: string, last_name: string, wustl_key: string, bear_bucks: real, courses: course list}
 +
 +
val bst = BinarySearchTree.create_empty(String.compare, (fn(s:student) => (#wustl_key s)))
 +
val (bst, _) = BinarySearchTree.insert(bst, {first_name="Bruce", last_name="Wayne", wustl_key="wayne.b", bear_bucks=999999.99, courses=[("Business", 101)]})
 +
val (bst, _) = BinarySearchTree.insert(bst, {first_name="Peter", last_name="Parker", wustl_key="webslinger", bear_bucks=12.34, courses=[("Biology", 101)]})
 +
val (bst, _) = BinarySearchTree.insert(bst, {first_name="Diana", last_name="Prince", wustl_key="amazon_diana", bear_bucks=234.56, courses=[("Anthropology", 101)]})
 +
val (bst, _) = BinarySearchTree.insert(bst, {first_name="Clark", last_name="Kent", wustl_key="i.m.superman", bear_bucks=34.56, courses=[("Journalism", 101)]})
 +
val (bst, _) = BinarySearchTree.insert(bst, {first_name="Bruce", last_name="Banner", wustl_key="gamma.ray", bear_bucks=456.78, courses=[("Physics", 101)]})</nowiki>
 +
 +
[[File:Bst example supers.svg]]
 +
 +
==student record example with int as key==
 +
 +
<nowiki>datatype department = COMPUTER_SCIENCE | ENGLISH | ARCHITECTURE | BIOCHEMISTRY
 +
type student = {id: int, name: string, major: department}
 +
 +
val bst = BinarySearchTree.create_empty(Int.compare, fn(s:student) => #id s)
 +
val (bst,_) = BinarySearchTree.insert(bst, {id=401936, name="Tennessee Williams", major=ENGLISH})
 +
val (bst,_) = BinarySearchTree.insert(bst, {id=401927, name="Charles Eams", major=ARCHITECTURE})
 +
val (bst,_) = BinarySearchTree.insert(bst, {id=401991, name="Rochelle Walensky", major=BIOCHEMISTRY})</nowiki>
 +
 +
[[File:Bst example students.svg]]
 +
 
==order==
 
==order==
−
SML's General structure's [http://sml-family.org/Basis/general.html#SIG:GENERAL.order:TY order]
+
SML's General structure's [https://smlfamily.github.io/Basis/general.html#SIG:GENERAL.order:TY order]
−
datatype order = LESS | EQUAL | GREATER
+
<syntaxhighlight lang="sml">
 +
datatype order = LESS | EQUAL | GREATER
 +
</syntaxhighlight>
 
Values of type order are used when comparing elements of a type that has a linear ordering.
 
Values of type order are used when comparing elements of a type that has a linear ordering.
  
−
Functions which take (('a * 'a) -> order) functions behave as [http://sml-family.org/Basis/integer.html#SIG:INTEGER.compare:VAL Int.compare] does:
+
Functions which take (('k * 'k) -> order) functions behave as [https://smlfamily.github.io/Basis/integer.html#SIG:INTEGER.compare:VAL Int.compare] does:
 
: compare (i, j)
 
: compare (i, j)
 
:: returns LESS, EQUAL, or GREATER when i is less than, equal to, or greater than j, respectively.
 
:: returns LESS, EQUAL, or GREATER when i is less than, equal to, or greater than j, respectively.
  
 
==list==
 
==list==
−
We will implement some of the higher ordered functions [http://sml-family.org/Basis/list.html list] provides on our binary tree.
+
We will implement some of the higher ordered functions [https://smlfamily.github.io/Basis/list.html list] provides on our binary tree.
  
 
==traversal order==
 
==traversal order==
−
[[File:Sorted binary tree inorder.svg|Sorted binary tree inorder|frame|LNR would produce: ABCDEFGHI<br>RNL would produce: IHGFEDCBA]]
+
* [https://en.wikipedia.org/wiki/Tree_traversal#In-order_(LNR) In-order LNR]
−
[https://en.wikipedia.org/wiki/Tree_traversal#In-order_(LNR) In-order LNR]
+
 
 +
* [https://en.wikipedia.org/wiki/Tree_traversal#In-order_(RNL) Reverse in-order RNL]
 +
 
 +
=Code to Implement=
 +
{{SMLToImplement|binary_tree|create_empty<br/>find<br/>insert<br/>remove<br/>fold_lnr<br/>fold_rnl<br/>debug_message<br/>to_graphviz_dot|binary_tree}}
 +
 
 +
<syntaxhighlight lang="sml">
 +
signature BINARY_SEARCH_TREE = sig
 +
    type 'k compare_function = (('k * 'k) -> order)
 +
    type ('e,'k) to_key_function = 'e -> 'k
 +
 
 +
    type ('e,'k) tree;
 +
 
 +
    val create_empty : ('k compare_function * ('e,'k) to_key_function) -> ('e,'k) tree
 +
 
 +
    val find : (('e,'k) tree * 'k) -> 'e option
 +
    val insert : (('e,'k) tree * 'e) -> (('e,'k) tree * 'e option)
 +
    val remove : (('e,'k) tree * 'k) -> (('e,'k) tree * 'e option)
 +
 
 +
    val fold_lnr : ((('e * 'b) -> 'b) * ('b) * (('e,'k) tree)) -> 'b
 +
    val fold_rnl : ((('e * 'b) -> 'b) * ('b) * (('e,'k) tree)) -> 'b
 +
   
 +
    val debug_message : (('e -> string) * (('e,'k) tree)) -> string
 +
    val to_graphviz_dot : (('e -> string) * ('k -> string) * (('e,'k) tree)) -> string
 +
end
 +
</syntaxhighlight>
 +
 
 +
==type==
 +
===provided compare_function and to_key_function type synonyms===
 +
<syntaxhighlight lang="sml">
 +
type 'k compare_function = (('k * 'k) -> order)
 +
type ('e,'k) to_key_function = 'e -> 'k
 +
</syntaxhighlight>
  
−
[https://en.wikipedia.org/wiki/Tree_traversal#In-order_(RNL) Reverse in-order RNL]
+
===required (at minimum) tree===
 +
<syntaxhighlight lang="sml">
  
−
  datatype traversal_order = LNR | RNL
+
(* TODO: replace unit with the datatype(s) and/or type synonym(s) you decide upon *)
 +
type ('a,'k) tree = unit
 +
</syntaxhighlight>
  
−
=BinaryTree=
+
==create_empty==
−
{{SMLToImplement|binary_tree|insert<br/>remove<br/>find<br/>...|binary_tree}}
+
<syntaxhighlight lang="sml">
 +
fun create_empty(cmp : 'k compare_function, to_key : ('e,'k) to_key_function) : ('e,'k) tree =
 +
raise Fail("NotYetImplemented")
 +
</syntaxhighlight>
  
−
datatype 'a tree = LEAF | BRANCH of 'a tree * 'a * 'a tree
+
==find==
−
==core==
+
reference: [https://smlfamily.github.io/Basis/list.html#SIG:LIST.find:VAL List.find]
−
===insert===
 
−
{{CurriedFunction}}
 
−
fun insert (compare_function:(('a * 'a) -> order)) (t:'a tree) (item:'a) : 'a tree =
 
−
    raise NotYetImplemented
 
  
−
===remove===
+
<syntaxhighlight lang="sml">
−
{{CurriedFunction}}
+
fun find(t : ('e,'k) tree, key : 'k) : 'e option =  
−
fun remove (equal_less_greater_function:'a -> order) (t:'a tree) : 'a tree =
+
raise Fail("NotYetImplemented")
−
    raise NotYetImplemented
+
</syntaxhighlight>
  
−
===find===
+
==insert==
−
reference: [http://sml-family.org/Basis/list.html#SIG:LIST.find:VAL List.find]
+
<syntaxhighlight lang="sml">
 +
fun insert(t : ('e,'k) tree, element : 'e) : (('e,'k) tree * 'e option) =
 +
raise Fail("NotYetImplemented")
 +
</syntaxhighlight>
  
−
{{CurriedFunction}}
+
NOTE: if the key for the specified item matches a key already in the tree, the previous item is replaced.
−
fun find (equal_less_greater_function : 'a -> order) (t:'a tree) : 'a option =
 
−
    raise NotYetImplemented
 
  
−
==fun==
+
NOTE: it is critical to build the tree "on the way out" of the recursion.  This is much like one must build the list "on the way out" in the [[Remove_First_Assignment| Remove First]] and [[Eliminate_Unsorted_Assignment|Eliminate Unsorted]] assignments.
−
===to_first_and_last===
 
−
This function is useful for find_order_hof and fold_order_hof.
 
  
−
It simply returns the left and right tree as a 2-tuple in the appropriate order based on the specified traversal_order.
+
<code>insert</code> returns a pair containing the new tree and the (optional) replaced value.
  
−
fun to_first_and_last(order:traversal_order, left:'a tree, right:'a tree) =
+
==remove==
−
    raise NotYetImplemented
+
<syntaxhighlight lang="sml">
 +
fun remove(t : ('e,'k) tree, key : 'k) : (('e,'k) tree * 'e option) =
 +
raise Fail("NotYetImplemented")</syntaxhighlight>
  
−
===find_order_hof===
+
<code>remove</code> the item whose key matches <code>item_key</code>, if it is found.
−
reference: [http://sml-family.org/Basis/list.html#SIG:LIST.find:VAL List.find]
 
  
−
Instead of a binary search style find, here we create a find based on a traversal order and a predicate.  It returns the first item node value it encounters which passes the predicate function.
+
returns a pair of the modified tree and the (optional) removed item.
  
−
{{CurriedFunction}}
+
Remove contains the most challenging aspect of this studio. When instructed to remove a node from a tree, there are several cases:
−
  fun find_order_hof (order:traversal_order) (predicate:'a->bool) (t:'a tree) : 'a option =
 
−
    raise NotYetImplemented
 
  
−
fun find_lnr (predicate:'a->bool) (t:'a tree) : 'a option =  
+
===not found===
−
    find_order_hof LNR predicate t
+
What will indicate that you reached the point where you know the node is not found in the tree?<br>note: this has a trivial solution.
−
fun find_rnl (predicate:'a->bool) (t:'a tree) : 'a option =  
+
===no child in the left tree===
−
    find_order_hof RNL predicate t
+
How will you detect this pattern?<br>note: this has a trivial solution.
 +
===no child in the right tree===
 +
how will you detect this pattern?<br>note: this has a trivial solution.
 +
===both children are present===
 +
If you need to remove a node and it has both children, now you have a legit problem.  You must maintain a correct binary search tree.
  
−
===fold_order_hof===
+
====standard approach====
−
reference: [http://sml-family.org/Basis/list.html#SIG:LIST.foldl:VAL List.foldl]
+
A common approach is to choose one of the following:
 +
* remove the right most descendant in the left child, and promote it to be the node at the current level, or
 +
* remove the left most descendant in the right child, and promote it to be the node at the current level
  
−
{{CurriedFunction}}
+
The image below shows finding the left most child in the right subtree for promotion:
−
fun fold_order_hof (order:traversal_order) (f : 'a * 'b -> 'b) (init : 'b) (t : 'a tree) : 'b =
 
−
    raise NotYetImplemented
 
  
−
fun fold_lnr f init t =
+
[[File:AVL-tree-delete.svg|600px]]
−
    fold_order_hof LNR f init t
 
−
fun fold_rnl f init t =
 
−
    fold_order_hof RNL f init t
 
−
===filter (Not Required)===
 
−
reference: [http://sml-family.org/Basis/list.html#SIG:LIST.filter:VAL List.filter]
 
  
−
{{CurriedFunction}}
+
Building a helper function will likely be helpful.
−
fun filter (predicate : 'a -> bool) (t : 'a tree) : 'a tree =
 
−
    raise NotYetImplemented
 
  
−
===filter_civil_war_style===
+
[https://en.wikipedia.org/wiki/Binary_search_tree#Deletion Wikipedia BST Deletion]
−
This function is much like filter, only instead of deftly omitting the nodes which do not pass the predicate, it lops off the entire subtree of those nodes which do not pass the predicate.
 
  
−
{{CurriedFunction}}
+
====alternate approach?====
−
fun filter_civil_war_style (predicate : 'a -> bool) (t : 'a tree) : 'a tree =
+
Can you come up with a different approach that produces a clean solution while still providing O(lg(N)) expected performance?
−
    raise NotYetImplemented
 
  
−
===map_to_tree_of_questionable_validity===
+
==fold==
−
reference: [http://sml-family.org/Basis/list.html#SIG:LIST.map:VAL List.map]
+
reference: [https://smlfamily.github.io/Basis/list.html#SIG:LIST.foldl:VAL List.foldl] [https://smlfamily.github.io/Basis/list.html#SIG:LIST.foldr:VAL foldr]
  
−
This function converts the specified 'a tree into a 'b tree. It is unreasonable to expect the resulting tree (which is to have the same structure as the specified 'a tree) will be a valid binary search tree.
+
[[File:Sorted binary tree inorder.svg|Sorted binary tree inorder|frame|LNR would produce: ABCDEFGHI<br>RNL would produce: IHGFEDCBA]]
  
−
{{CurriedFunction}}
+
===fold_lnr===
−
  fun map_to_tree_of_questionable_validity (f : 'a -> 'b) (t : 'a tree) : 'b tree =  
+
<syntaxhighlight lang="sml">
−
    raise NotYetImplemented
+
(*
 +
* depth-first, in-order traversal
 +
* https://en.wikipedia.org/wiki/Tree_traversal#In-order_(LNR)
 +
*)
 +
fun fold_lnr(f, init, t) =
 +
raise Fail("NotYetImplemented")
 +
</syntaxhighlight>
 +
===fold_rnl===
 +
<syntaxhighlight lang="sml">
 +
(*
 +
* depth-first, reverse in-order traversal
 +
* https://en.wikipedia.org/wiki/Tree_traversal#Reverse_in-order_(RNL)
 +
*)
 +
fun fold_rnl(f, init, t) =  
 +
raise Fail("NotYetImplemented")
 +
</syntaxhighlight>
  
−
===map_to_tree_hof (Not Required)===
+
=Debugging=
−
{{CurriedFunction}}
+
Visualizing the state of the tree often helps with debugging. We have provided a skeleton which can be adapted to your particular type declaration(s).
−
  fun map_to_tree_hof (order:traversal_order) (compare_function:(('b * 'b) -> order)) (f : 'a -> 'b) (t : 'a tree) : 'b tree =
 
−
    raise NotYetImplemented
 
  
−
fun map_to_tree_lnr compare_function f t =  
+
==BinarySearchTree==
−
    map_to_tree_hof LNR compare_function f t
+
===to_graphviz_dot===
−
fun map_to_tree_rnl compare_function f t =  
+
<syntaxhighlight lang=java>
−
    map_to_tree_hof RNL compare_function f t
+
fun to_graphviz_dot(element_to_string, key_to_string, t) =
 +
let
 +
 +
(* TODO: bind root *)
 +
val root = raise Fail("NotYetImplemented")
 +
(* TODO: bind to_key *)
 +
val to_key = raise Fail("NotYetImplemented")
 +
  
−
===map_to_list_hof (Not Required)===
+
fun nodes_to_dot(bst) =
−
{{CurriedFunction}}
+
let
−
fun map_to_list_hof (order:traversal_order) (f : 'a -> 'b) (t : 'a tree) : 'b list =
+
fun empty_to_string() =
−
    raise NotYetImplemented
+
""
 +
fun present_to_string(left, element, right) =
 +
let
 +
fun node_to_dot(element) =
 +
"\t" ^ key_to_string(to_key(element)) ^ " [label= \"{ " ^ element_to_string(element) ^ " | { <child_left> | <child_right> } }\"]"
 +
in
 +
node_to_dot(element) ^ "\n" ^ nodes_to_dot(left) ^ nodes_to_dot(right)
 +
end
 +
in
 +
raise Fail("NotYetImplemented")
 +
end
  
−
fun map_to_list_lnr f t =  
+
fun edges_to_dot(bst, parent_element_opt, tag) =
−
    map_to_list_hof LNR f t
+
let
−
fun map_to_list_rnl f t =  
+
fun empty_to_string() =
−
    map_to_list_hof RNL f t
+
""
 +
fun present_to_string(left, element, right) =
 +
let
 +
fun edge_to_dot(parent_element_opt, tag, element) =
 +
case parent_element_opt of
 +
NONE => ""
 +
| SOME(parent_element) => "\t" ^ key_to_string(to_key(parent_element)) ^ tag ^ " -> " ^ key_to_string(to_key(element))
 +
in
 +
edge_to_dot(parent_element_opt, tag, element) ^ "\n" ^ edges_to_dot(left, SOME(element), ":child_left:center") ^ edges_to_dot(right, SOME(element), ":child_right:center")
 +
end
 +
in
 +
raise Fail("NotYetImplemented")
 +
end
 +
in
 +
"digraph g {\n\n\tnode [\n\t\tshape = record\n\t]\n\n\tedge [\n\t\ttailclip=false,\n\t\tarrowhead=vee,\n\t\tarrowtail=dot,\n\t\tdir=both\n\t]\n\n" ^ nodes_to_dot(root) ^ edges_to_dot(root, NONE, "") ^ "\n}\n"
 +
end
 +
</syntaxhighlight>
  
−
=Applications=
+
==debug_binary_search_tree==
−
{{SMLToImplement|apps_using_binary_tree|max_height<br/>sum_int_tree|binary_tree}}
+
file:  <code>debug_binary_search_tree.sml</code>
−
==max_height==
+
 
−
  fun max_height(t : 'a BinaryTree.tree) : int =
+
in folder: <code>src/test/sml/run_binary_search_tree_testing</code>
−
  raise NotYetImplemented
+
 
−
==sum_int_tree==
+
==graphviz dot extenstion in visual studio code==
−
fun sum_int_tree(t : int BinaryTree.tree) : int =
+
search for "graphviz dot" in vs code extensions marketplace
−
  raise NotYetImplemented
 
  
 
=Testing=
 
=Testing=
−
{{SMLUnitTest|binary_tree_and_apps|binary_tree}}
+
==Complete==
 +
{{SMLUnitTesting|run_bst_testing|binary_search_tree}}
 +
==Without Remove==
 +
sml -Ccm.verbose=false run_bst_testing.sml --remove=false
 +
 
 +
sml run_bst_testing.sml --remove=false
  
 
=Pledge, Acknowledgments, Citations=
 
=Pledge, Acknowledgments, Citations=
−
{{Pledge|studio-binary-tree}}
+
{{Pledge|studio-binary-search-tree}}

Latest revision as of 17:18, 26 October 2023

We will implement a binary search tree data structure as well as Higher Order Function Hall of Fame inductees: find and fold.

Background

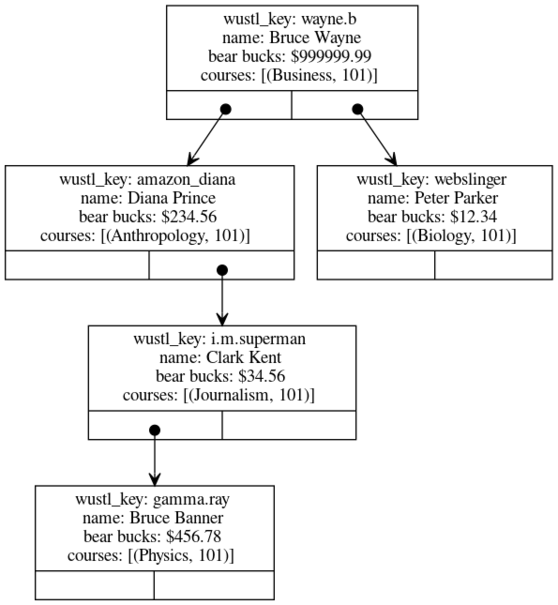
student record example

type course = (string*int)
type student = {first_name: string, last_name: string, wustl_key: string, bear_bucks: real, courses: course list}

val bst = BinarySearchTree.create_empty(String.compare, (fn(s:student) => (#wustl_key s)))
val (bst, _) = BinarySearchTree.insert(bst, {first_name="Bruce", last_name="Wayne", wustl_key="wayne.b", bear_bucks=999999.99, courses=[("Business", 101)]})
val (bst, _) = BinarySearchTree.insert(bst, {first_name="Peter", last_name="Parker", wustl_key="webslinger", bear_bucks=12.34, courses=[("Biology", 101)]})
val (bst, _) = BinarySearchTree.insert(bst, {first_name="Diana", last_name="Prince", wustl_key="amazon_diana", bear_bucks=234.56, courses=[("Anthropology", 101)]})
val (bst, _) = BinarySearchTree.insert(bst, {first_name="Clark", last_name="Kent", wustl_key="i.m.superman", bear_bucks=34.56, courses=[("Journalism", 101)]})
val (bst, _) = BinarySearchTree.insert(bst, {first_name="Bruce", last_name="Banner", wustl_key="gamma.ray", bear_bucks=456.78, courses=[("Physics", 101)]})

Bst example supers.svg

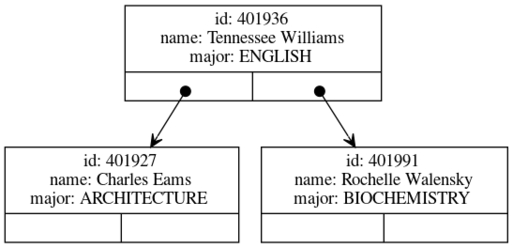
student record example with int as key

datatype department = COMPUTER_SCIENCE | ENGLISH | ARCHITECTURE | BIOCHEMISTRY
type student = {id: int, name: string, major: department}

val bst = BinarySearchTree.create_empty(Int.compare, fn(s:student) => #id s)
val (bst,_) = BinarySearchTree.insert(bst, {id=401936, name="Tennessee Williams", major=ENGLISH})
val (bst,_) = BinarySearchTree.insert(bst, {id=401927, name="Charles Eams", major=ARCHITECTURE})
val (bst,_) = BinarySearchTree.insert(bst, {id=401991, name="Rochelle Walensky", major=BIOCHEMISTRY})

Bst example students.svg

order

SML's General structure's order 

datatype order = LESS | EQUAL | GREATER

Values of type order are used when comparing elements of a type that has a linear ordering.

Functions which take (('k * 'k) -> order) functions behave as Int.compare does:

compare (i, j)
returns LESS, EQUAL, or GREATER when i is less than, equal to, or greater than j, respectively.

list

We will implement some of the higher ordered functions list provides on our binary tree.

traversal order

Code to Implement

file: src/main/sml/binary_tree/binary_tree.sml Smlnj-logo.png
functions: create_empty
find
insert
remove
fold_lnr
fold_rnl
debug_message
to_graphviz_dot		 
signature BINARY_SEARCH_TREE = sig
    type 'k compare_function = (('k * 'k) -> order)
    type ('e,'k) to_key_function = 'e -> 'k

    type ('e,'k) tree;

    val create_empty : ('k compare_function * ('e,'k) to_key_function) -> ('e,'k) tree

    val find : (('e,'k) tree * 'k) -> 'e option
    val insert : (('e,'k) tree * 'e) -> (('e,'k) tree * 'e option)
    val remove : (('e,'k) tree * 'k) -> (('e,'k) tree * 'e option)

    val fold_lnr : ((('e * 'b) -> 'b) * ('b) * (('e,'k) tree)) -> 'b 
    val fold_rnl : ((('e * 'b) -> 'b) * ('b) * (('e,'k) tree)) -> 'b 
    
    val debug_message : (('e -> string) * (('e,'k) tree)) -> string
    val to_graphviz_dot : (('e -> string) * ('k -> string) * (('e,'k) tree)) -> string
end

type

provided compare_function and to_key_function type synonyms

type 'k compare_function = (('k * 'k) -> order)
type ('e,'k) to_key_function = 'e -> 'k

required (at minimum) tree

(* TODO: replace unit with the datatype(s) and/or type synonym(s) you decide upon *)
type ('a,'k) tree = unit

create_empty

fun create_empty(cmp : 'k compare_function, to_key : ('e,'k) to_key_function) : ('e,'k) tree =
	raise Fail("NotYetImplemented")

find

reference: List.find 

fun find(t : ('e,'k) tree, key : 'k) : 'e option = 
	raise Fail("NotYetImplemented")

insert

fun insert(t : ('e,'k) tree, element : 'e) : (('e,'k) tree * 'e option) =
	raise Fail("NotYetImplemented")

NOTE: if the key for the specified item matches a key already in the tree, the previous item is replaced.

NOTE: it is critical to build the tree "on the way out" of the recursion. This is much like one must build the list "on the way out" in the Remove First and Eliminate Unsorted assignments.

insert returns a pair containing the new tree and the (optional) replaced value.

remove

fun remove(t : ('e,'k) tree, key : 'k) : (('e,'k) tree * 'e option) =
	raise Fail("NotYetImplemented")

remove the item whose key matches item_key, if it is found.

returns a pair of the modified tree and the (optional) removed item.

Remove contains the most challenging aspect of this studio. When instructed to remove a node from a tree, there are several cases:

not found

What will indicate that you reached the point where you know the node is not found in the tree?
note: this has a trivial solution.

no child in the left tree

How will you detect this pattern?
note: this has a trivial solution.

no child in the right tree

how will you detect this pattern?
note: this has a trivial solution.

both children are present

If you need to remove a node and it has both children, now you have a legit problem. You must maintain a correct binary search tree.

standard approach

A common approach is to choose one of the following:

  • remove the right most descendant in the left child, and promote it to be the node at the current level, or
  • remove the left most descendant in the right child, and promote it to be the node at the current level

The image below shows finding the left most child in the right subtree for promotion:

AVL-tree-delete.svg

Building a helper function will likely be helpful.

Wikipedia BST Deletion

alternate approach?

Can you come up with a different approach that produces a clean solution while still providing O(lg(N)) expected performance?

fold

reference: List.foldl foldr

LNR would produce: ABCDEFGHI
RNL would produce: IHGFEDCBA

fold_lnr

(*
 * depth-first, in-order traversal
 * https://en.wikipedia.org/wiki/Tree_traversal#In-order_(LNR)
 *)
fun fold_lnr(f, init, t) = 
	raise Fail("NotYetImplemented")

fold_rnl

(*
 * depth-first, reverse in-order traversal
 * https://en.wikipedia.org/wiki/Tree_traversal#Reverse_in-order_(RNL)
 *)
fun fold_rnl(f, init, t) = 
	raise Fail("NotYetImplemented")

Debugging

Visualizing the state of the tree often helps with debugging. We have provided a skeleton which can be adapted to your particular type declaration(s).

BinarySearchTree

to_graphviz_dot

	fun to_graphviz_dot(element_to_string, key_to_string, t) =
		let
			
			(* TODO: bind root *)
			val root = raise Fail("NotYetImplemented")
			(* TODO: bind to_key *)
			val to_key = raise Fail("NotYetImplemented")
			

			fun nodes_to_dot(bst) =
				let
					fun empty_to_string() =
						""
					fun present_to_string(left, element, right) =
						let
							fun node_to_dot(element) =
								"\t" ^ key_to_string(to_key(element)) ^ " [label= \"{ " ^ element_to_string(element) ^ " | { <child_left> | <child_right> } }\"]"
						in 
							node_to_dot(element) ^ "\n" ^ nodes_to_dot(left) ^ nodes_to_dot(right)
						end
				in
						raise Fail("NotYetImplemented")
				end

			fun edges_to_dot(bst, parent_element_opt, tag) =
				let
					fun empty_to_string() =
						""
					fun present_to_string(left, element, right) =
						let
							fun edge_to_dot(parent_element_opt, tag, element) = 
								case parent_element_opt of
								NONE => ""
								| SOME(parent_element) => "\t" ^ key_to_string(to_key(parent_element)) ^ tag ^ " -> " ^ key_to_string(to_key(element))
						in 
							edge_to_dot(parent_element_opt, tag, element) ^ "\n" ^ edges_to_dot(left, SOME(element), ":child_left:center") ^ edges_to_dot(right, SOME(element), ":child_right:center")
						end
				in
						raise Fail("NotYetImplemented")
				end
		in
			"digraph g {\n\n\tnode [\n\t\tshape = record\n\t]\n\n\tedge [\n\t\ttailclip=false,\n\t\tarrowhead=vee,\n\t\tarrowtail=dot,\n\t\tdir=both\n\t]\n\n" ^ nodes_to_dot(root) ^ edges_to_dot(root, NONE, "") ^ "\n}\n"
		end

debug_binary_search_tree

file: debug_binary_search_tree.sml

in folder: src/test/sml/run_binary_search_tree_testing

graphviz dot extenstion in visual studio code

search for "graphviz dot" in vs code extensions marketplace

Testing

Complete

source folder: src/test/sml/binary_search_tree
how to run with CM.make verbosity off: sml -Ccm.verbose=false run_bst_testing.sml
how to run with CM.make verbosity on: sml run_bst_testing.sml

note: ensure that you have removed all printing to receive credit for any assignment.

SML Error Messages

Without Remove

sml -Ccm.verbose=false run_bst_testing.sml --remove=false

sml run_bst_testing.sml --remove=false

Pledge, Acknowledgments, Citations

file: studio-binary-search-tree-pledge-acknowledgments-citations.txt

More info about the Honor Pledge

Retrieved from "http://classes.engineering.wustl.edu/cse425s/index.php?title=Binary_Search_Tree_Assignment&oldid=2248"