Simple beam models are used to verify unidirectional, cylindrical, and spherical gap elements.

GAPUNI with positive gap clearance:

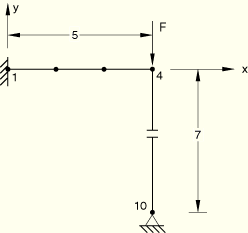
GAP data: Initial clearance = 0.5.

X, Y, Z direction cosine of the closure direction = (0., –1., 0.).

Boundary conditions: node 1 is clamped, and node 10 is fixed in the x- and y-directions.

Loading case 1: = –50 at node 4; Loading case 2: = –100 at node 4.

GAPCYL with positive gap clearance:

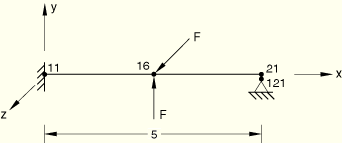
GAP data: Initial clearance = 0.0208 (positive gap clearance).

X, Y, Z direction cosine of the cylinder axis = (1., 0., 0.).

Boundary conditions: node 11 is clamped, node 121 is fixed in the x-, y- and z-directions.

Loading: Step 1: = 2.0 × 10⁴ at node 16; Step 2: = 3.0 × 10⁴ at node 16.

GAPCYL with negative gap clearance:

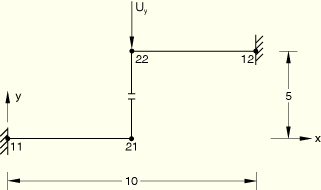
GAP data: Initial clearance = –1.0 (negative gap clearance).

X, Y, Z direction cosine of the cylinder axis = (1., 0., 0.).

Boundary conditions: nodes 11 and 12 are clamped, = –5.0 at node 22.

GAPSPHER with positive gap clearance:

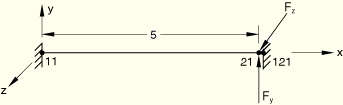
GAP data: Initial clearance = 0.2080.

Boundary conditions: nodes 11 and 121 are clamped.

Loading case 1: = 2.0 × 10⁴ and = 3.0 × 10⁴ at node 21; Loading case 2: = 4.0 × 10⁴ and = 6.0 × 10⁴ at node 21. The NLGEOM parameter is used.