1.3.17 Thermal stress in a cylindrical shell

Products: ABAQUS/Standard ABAQUS/Explicit

Elements tested

DSAX1 DSAX2 DS3 DS4 DS6 DS8 DCAX8 DC3D20

SAX1 SAX2 STRI65 S4R5 S8R5

CAX8R C3D20R

SAX2T S8RT CAX8RT CGAX8RT C3D20RT

CAX3T CAX4RT CAX4RHT CGAX4RT CGAX4RHT C3D4T C3D6T C3D8RT

Problem description

The cylindrical shell is shown above. A single element is used in the ABAQUS/Standard analyses. In the ABAQUS/Explicit analyses two elements are used in the radial direction. For the nonaxisymmetric elements the element subtends an angle of 11.25° at the center, which is equivalent to 32 elements around the circumference.

Steady-state conditions are assumed in the ABAQUS/Standard simulation. A transient simulation is performed in ABAQUS/Explicit. The total simulation time is 0.4 seconds. This provides enough time for the transient solution to reach steady-state conditions in this problem. Mass scaling is used to reduce the computational cost of the ABAQUS/Explicit analyses.

Material:

Density	7800 kg/m³
Conductivity	52 J/ms °C
Specific heat	586 J/kg °C
Thermal expansion coefficient	1.2 × 10^–5
Young's modulus	200 × 10³ MPa
Poisson's ratio	0.3

Boundary conditions:

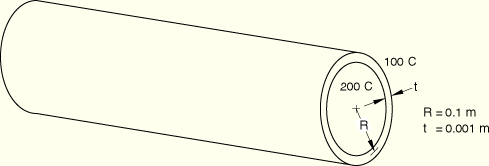
For the thermal analyses the temperatures of the inside and outside surfaces are prescribed to be 200°C and 100°C, respectively. For the stress analyses the rotation vector in the circumferential direction is constrained, but the cylinder is free to expand axially. For the continuum element meshes equations are used to provide the rotational constraints. For the nonaxisymmetric cases symmetrical constraints are applied in the circumferential direction to model the complete cylinder.

In the ABAQUS/Explicit simulations the temperatures are applied gradually to ensure a quasi-static response.

For all of the analyses except those using the coupled temperature-displacement elements (SAX2T, S8RT, CAX4RT, CAX4RHT, CGAX4RT, CGAX4RHT, CAX8RT, CGAX8RT, and C3D20RT in ABAQUS/Standard and CAX3T, CAX4RT, C3D4T, C3D6T, and C3D8RT in ABAQUS/Explicit), the analyses are run in pairs: a thermal analysis followed by its corresponding stress analysis.

Gauss integration is used for the shell cross-section for input file es54sxsj.inp.

Reference solution

The temperature distribution through the thickness of the cylinder is given by

where

is the outer radius,

is the inner radius,

is the outside temperature, and

is the inside temperature.

The analytical solution for the stresses is given in Chapter 15 of “Theory of Plates and Shells,” second edition, by Timoshenko and Woinowsky-Krieger. The stresses at the outer and inner surfaces are given by

where E is Young's modulus,

is the coefficient of thermal expansion, and

is Poisson's ratio. The upper sign refers to the outer surface, indicating that a tensile stress will act on this surface if

This gives a theoretical stress of 171.43 MPa.

Results and discussion

The axisymmetric and second-order shell elements agree exactly with the theory. The first-order three-dimensional shells (S4R5) show an error of –5.1%. The continuum elements show small discrepancies (< 1%) from the reference solution.

The results obtained with ABAQUS/Explicit are in close agreement with those obtained with ABAQUS/Standard.